
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Электрических аппаратов
|
|
Источники теплоты в электрических аппаратах при их работе образуют тепловое поле:

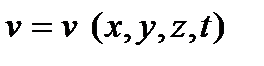 . (11)
. (11)
В общем случае задачей теплового расчета является определение мощности источников теплоты и расчет параметров температурного поля. При этом максимальная температура не должна превышать допустимую, которая зависит от многих факторов и устанавливается стандартами.
Можно выделить три задачи теплового расчета.
Первая – расчет мощности источников теплоты P.
Вторая - расчет зависимости температуры фиксированной координаты в пространстве (например, поверхности аппарата) от времени v(t).
Третья – расчет зависимости температуры вдоль линейной координаты. Например, распределение температуры по ширине катушки или по толщине какой-либо стенки аппарата, определение координаты с максимальной температурой в этой же стенке аппарата. После решения одной из трех перечисленных задач или всех трех встает вопрос оптимизации теплового режима аппарата.
Существует несколько способов уменьшения мощности источников теплоты в электрических аппаратах. Например, применяют проводниковые материалы с малым удельным сопротивлением, используют трубчатые проводники (для снижения поверхностного эффекта), применяют короткозамкнутые витки для снижения действия вихревых токов и так далее.
Кроме уменьшения мощности источников теплоты, необходимо искать пути уменьшения максимальной температуры в аппарате.
Исходя из формулы Ньютона (10), можно уменьшить температуру поверхности тела v за счет увеличения коэффициента теплоотдачи KT или площади Sохл при постоянных значениях мощности Р и температуры окружающей среды v0. Такой способ уменьшения температуры называется интенсификацией охлаждения.
Увеличение коэффициента теплоотдачи КТ можно добиться покраской нагреваемых частей аппарата краской, имеющей больший коэффициент излучения ε, чем поверхность, которая не была окрашена. Кроме того, КТ можно увеличить за счет вынужденной конвекции, или жидкостным охлаждением.
Рассмотрим переходной процесс нагрева аппарата. Вмомент времени t = 0 при начальной температуре 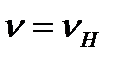 мощность источников теплоты определяется выражением
мощность источников теплоты определяется выражением 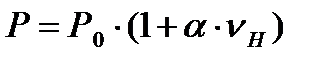 .
.
Из анализа теплового баланса можно получить дифференциальное уравнение, решение которого при
КТ.SОХЛ ≠ Р0. α имеет вид: 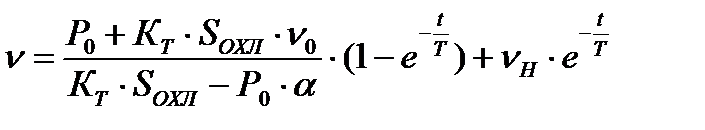
 , (12)
, (12)
где Т – постоянная времени нагрева (имеет размерность времени),  .
.
Если 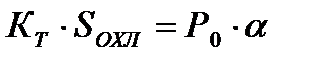 , то уравнение нагрева:
, то уравнение нагрева:
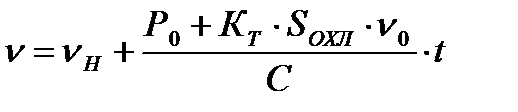 , (13)
, (13)
где С – теплоёмкость.
Графически кривые нагрева, т.е. зависимости (12) и (13) представлены на рис. 3.
При 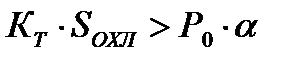 , Т > 0 величина
, Т > 0 величина
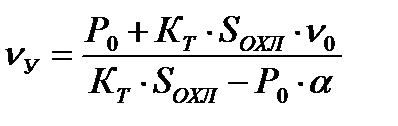 (14)
(14)
называется установившимся значением температуры.
Тогда выражение (12) можно упростить:
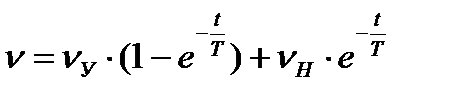 . (15)
. (15)
Если начальная температура аппарата равна температуре окружающей среды  , а разность температур θ =
, а разность температур θ = 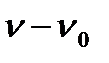 , θ У =
, θ У = 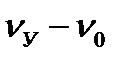 , то кривая нагрева (15) описывается уравнением:
, то кривая нагрева (15) описывается уравнением:
θ = θУ 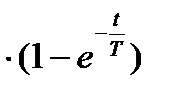 (16)
(16)
и представлена на рис. 1.4 кривой – 1.
При остывании аппарата температурная зависимость:
θ = θН 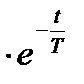 , (17)
, (17)
где θН= 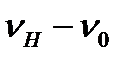 , имеет вид затухающей экспоненты (рис.4) кривая-2).
, имеет вид затухающей экспоненты (рис.4) кривая-2).
θ
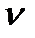
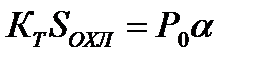
θУ

|
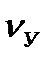

|
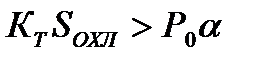 θН 1
θН 1
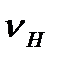 2
2
0 t 0 t
Рис. 4 Рис. 3
Рассмотрим задачу расчёта температурного поля в частях электрических аппаратов вдоль выбранной координаты в пространстве.
Из уравнения Фурье (7), описывающего теплопроводность, можно получить общее решение для установившегося теплового режима плоской стенки без внутренних источников теплоты
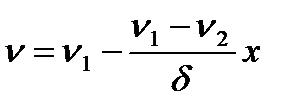 , (18)
, (18)
где 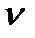 - температура в произвольной точке стенки толщиной
- температура в произвольной точке стенки толщиной 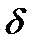 ,
,
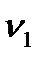 - температура при х = 0,
- температура при х = 0, 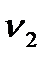 - температура при х =
- температура при х = 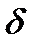 , если
, если 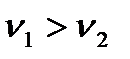 (рис. 5).
(рис. 5).
 Из закона Фурье (7) и (18) можно получить уравнение, называемое законом Ома для теплопроводности (19).
Из закона Фурье (7) и (18) можно получить уравнение, называемое законом Ома для теплопроводности (19).
 , (19)
, (19)
где Р – тепловой поток (аналогия с электрическим током), 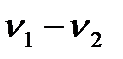 - разность температур (аналогия с разностью электрических потенциалов), RT – тепловое сопротивление.
- разность температур (аналогия с разностью электрических потенциалов), RT – тепловое сопротивление.
По аналогии с электрическим сопротивлением
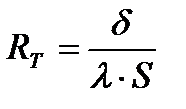 , (20)
, (20)
где 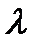 - теплопроводность материала стенки (аналогия с электропроводностью, или проводимостью 1 /ρ); S- площадь стенки.
- теплопроводность материала стенки (аналогия с электропроводностью, или проводимостью 1 /ρ); S- площадь стенки.
Учитывая приведенную аналогию, можно составить эквивалентную схему замещения (рис. 6).
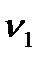 RТ
RТ 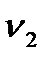 Если плоская стенка заключена между
Если плоская стенка заключена между
О О двумя окружающими средами: с одной
Р стороны температура 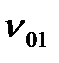 и коэффициент
и коэффициент
Рис. 6 теплоотдачи 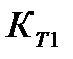 , с другой стороны
, с другой стороны
температура 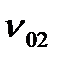 и коэффициент теплоотдачи
и коэффициент теплоотдачи 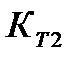 , то
, то
эквивалентная схема замещения и кривая распределения температур имеет вид, представленный на рис. 7.
| Рис. 7 |
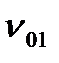 к стенке и от стенки к среде с температурой
к стенке и от стенки к среде с температурой 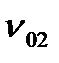 . Тепловое сопротивление теплоотдачи конвекцией RTК определяется по формуле Ньютона (10)
. Тепловое сопротивление теплоотдачи конвекцией RTК определяется по формуле Ньютона (10) RTК = 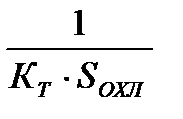 . (21)
. (21)
В электрических аппаратах часто встречаются стенки с равномерно распределенными источниками теплоты. Например, катушка, по которой проходит электрический ток. Каждый виток катушки – это источник теплоты.
Внутри стенки с источниками теплоты есть слой - координата Xmax с максимальной температурой vmax.
Координата такого слоя определяется по формуле Сливинской А.Г.:
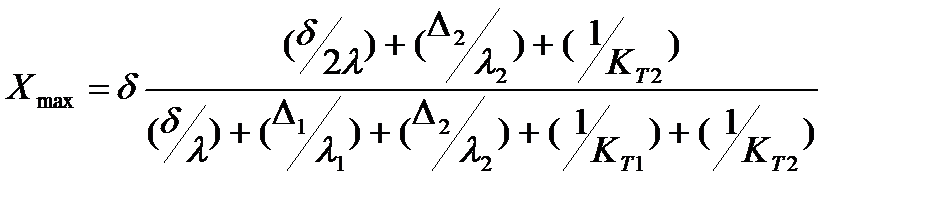 , (22)
, (22)
где  - толщина
- толщина 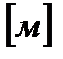 ,
, 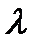 - теплопроводность стенки
- теплопроводность стенки 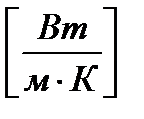 ,
, 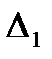 и
и 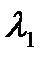 -толщина
-толщина 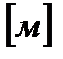 и теплопроводность
и теплопроводность 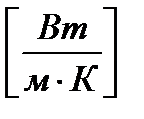 левой изоляционной стенки без источников теплоты;
левой изоляционной стенки без источников теплоты; 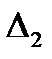 и
и 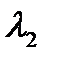 - правой стенки без источников; KT1 и KT2 – коэффи-циенты теплоотдачи с левой и правой изоляционных стенок в окружающую среду. Кривая распределения температуры приведена на рис 8.
- правой стенки без источников; KT1 и KT2 – коэффи-циенты теплоотдачи с левой и правой изоляционных стенок в окружающую среду. Кривая распределения температуры приведена на рис 8.
Для цилиндрической стенки с равномерно распределенными источниками теплоты (рис 9) радиус наиболее нагретого слоя определяется из выражения:
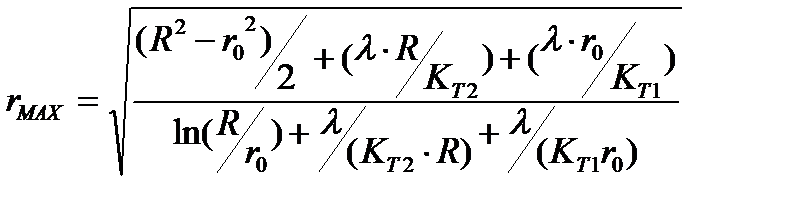 . (23)
. (23)
Плоские катушки электрических аппаратов без магнитопроводов рассчитываются как стенки с равномерно распределенными источниками теплоты, а цилиндрические катушки – как цилиндрические стенки.
Объемная плотность источников теплоты в катушке определяется из выражения:
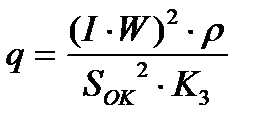 , (24)
, (24)
где IW - магнитодвижущая сила, А;
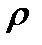 - удельное электрическое сопротивление материала проводника катушки, Ом
- удельное электрическое сопротивление материала проводника катушки, Ом  м;
м;
SОК - площадь обмоточного окна, м2;
K3 - коэффициент заполнения обмоточного окна.
| Рис. 9 |
| Рис. 8 |
Для определения теплопроводности катушки используют эмпирические формулы для разных типов катушек: непропитанных и пропитанных, при рядовой намотке или шахматной.
Алгоритм расчета распределения температур по толщине стенки с равномерно распределенными источниками теплоты следующий:
- переходим к эквивалентной схеме замещения и вычисляем тепловые сопротивления RT1 , RT2 и т.д. по формулам (20, 21);
- определяем тепловой поток Р;
- определяем координату наиболее нагретого слоя;
- из закона Ома для теплового поля определяем разность температур: максимальной и окружающей среды
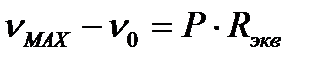 .
.
а также остальные температуры.
Date: 2015-07-27; view: 1204; Нарушение авторских прав