Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Основы построения ЭВМ. Элементы алгебры логики, зависимость числа выходов от числа входов
Основные принципы построения ЭВМ были сформулированы американским учёным Джоном фон Нейманом в 40-х годах 20 века:
1. Любую ЭВМ образуют три основные компоненты: процессор, память и устройства ввода-вывода (УВВ).
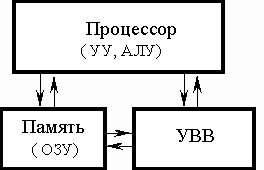
2. Информация, с которой работает ЭВМ делится на два типа:
· набор команд по обработке (программы);
· данные подлежащие обработке.
3. И команды, и данные вводятся в память (ОЗУ) – принцип хранимой программы.
4. Руководит обработкой процессор, устройство управления (УУ) которого выбирает команды из ОЗУ и организует их выполнение, а арифметико-логическое устройство (АЛУ) проводит арифметические и логические операции над данными.
5. С процессором и ОЗУ связаны устройства ввода-вывода (УВВ).
Архитектура современных персональных компьютеров основана на магистрально-модульном принципе. Информационная связь между устройствами компьютера осуществляется через системную шину (другое название - системная магистраль).
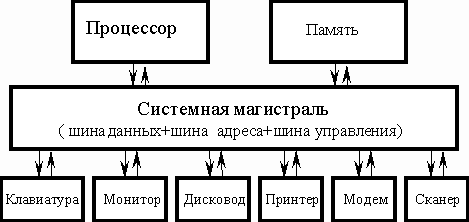
Схема устройства компьютера, построенного по магистральному принципу
Базовыми элементами, которыми оперирует алгебра логики, являются высказывания.
Высказывания строятся над множеством {B, 
, 
, 
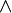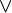, 0, 1}, где B — непустое множество, над элементами которого определены три операции:
отрицание (унарная операция),
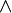конъюнкция (бинарная),
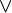дизъюнкция (бинарная),
а логический ноль 0 и логическая единица 1 — константы.
Таблица истинности для функций двух аргументов.
| x1=x | ||||||
| x0=y | Обозначение | Название | ||||
| F2,0 = 0 | тождественный ноль, детектор 0 | |||||
| F2,1 = x ↓ y = x NOR y = NOR(x, y) = x НЕ-ИЛИ y = НЕ-ИЛИ(x, y) | стрелка Пи́рса, НЕ-ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, функция Да́ггера, функция Ве́бба, детектор 1 | |||||
| F2,2 = x ← y = x < y = x LT y = LT(x, y) | инверсия обратной импликации, меньше, детектор 2 | |||||
| F2,3 = x = x' = x = NOT1(x, y) = НЕ1(x, y) | отрицание (негация, инверсия) первого операнда | |||||
| F2,4 = x → y = x > y = x GT y = GT(x, y) | инверсия прямой импликации, больше, детектор 4 | |||||
| F2,5 = y = y' = y = NOT2(x, y) = НЕ2(x, y) | отрицание (негация, инверсия) второго операнда | |||||
| F2,6 = x ⊕ y = x XOR y = XOR(x, y) = x >< y = x <> y = x NE y = NE(x,y) | сложение по модулю 2, исключающее «или», сумма Жегалкина[5], не равно | |||||
| F2,7 = x | y = x NAND y = NAND(x, y) = x НЕ-И y = НЕ-И(x, y) | штрих Ше́ффера, НЕ-И, 2И-НЕ, антиконъюнкция | |||||
| F2,8 = x ∧ y = x · y = xy = x & y = x AND y = AND(x, y) = x И y = И(x, y) = min(x, y) | конъюнкция, 2И, минимум, детектор 8 | |||||
| F2,9 = (x ≡ y) = x ~ y = x ↔ y = x EQV y = EQV(x, y) | эквивалентность, равенство | |||||
| F2,10 = YES2(x, y) = ДА2(x, y) = y | второй операнд | |||||
| F2,11 = x → y = x ⊃ y = x ≤ y = x LE y = LE(x, y) | прямая (материальная) импликация (от первого аргумента ко второму), меньше или равно | |||||
| F2,12 = YES1(x, y) = ДА1(x, y) = x | первый операнд | |||||
| F2,13 = x ← y = x ⊂ y = x ≥ y = x GE y = GE(x, y) | обратная импликация (от второго аргумента к первому), больше или равно | |||||
| F2,14 = x ∨ y = x + y = x OR y = OR(x, y) = x ИЛИ y = ИЛИ(x, y) = max(x, y) | дизъюнкция, 2ИЛИ, максимум | |||||
| F2,15 = 1 | тождественная единица, тавтология |
13. Схемы «И», «ИЛИ», «НЕ». Свойство логической полноты.
Схема И реализует конъюнкцию двух или более логических значений
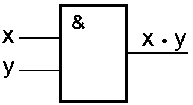
Схема ИЛИ реализует дизъюнкцию двух или более логических значений
Схема НЕ (инвертор) реализует операцию отрицания
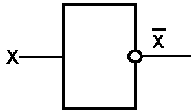
Теорема полноты. Для любой замкнутой формулы F и любого множества предложений G, если G влечёт F, то существует вывод F из некоторого подмножества G.
Date: 2015-07-27; view: 813; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |