
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Расчет доверительных интервалов и прогнозов для линейного уравнения регрессии
|
|
Как правило, в линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров.Показатели корреляционной связи, вычисленные по ограниченной совокупности (по выборке), являются лишь оценками той или иной статистической закономерности, поскольку в любом параметре сохраняется элемент не полностью погасившейся случайности, присущей индивидуальным значениям признаков. Поэтому необходима статистическая оценка степени точности и надежности параметров корреляции. Под надежностью здесь понимается вероятность того, что значение проверяемого параметра не равно нулю, не включает в себя величины противоположных знаков.
Вероятностная оценка параметров корреляции производится по общим правилам проверки статистических гипотез, разработанным математической статистикой, в частности путем сравнения оцениваемой величины со средней случайной ошибкой оценки. Для коэффициента парной регрессии b средняя ошибка оценки вычисляется как:
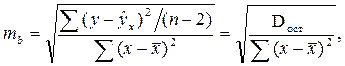
где Dост – остаточная дисперсия на одну степень свободы.
Для нашего примера величина стандартной ошибки коэффициента регрессии составила:
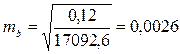 .
.
Для оценки того, насколько точные значения показателей могут отличаться от рассчитанных, осуществляется построение доверительных интервалов. Они определяют пределы, в которых лежат точные значения определяемых показателей с заданной степенью точности, соответствующей заданному уровню значимости α (α – вероятность отвергнуть правильную гипотезу при условии, что она верна, обычно принимается равной 0,05 или 0,01).
Для оценки статистической значимости коэффициента линейной регрессии и линейного коэффициента парной корреляции, а также для расчета доверительных интервалов b, применяется t – критерий Стьюдента.
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t-критерия Стьюдента: 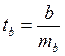 , которое затем сравнивается с табличным значением при определенном уровне значимости а и числе степеней свободы (n - 2).
, которое затем сравнивается с табличным значением при определенном уровне значимости а и числе степеней свободы (n - 2).
В рассматриваемом примере фактическое значение t-критерия для коэффициента регрессии составило:
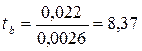 .
.
Этот же результат получим, извлекая квадратный корень из найденного F-критерия, т.е.
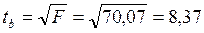 .
.
Действительно, справедливо равенство 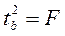 .
.
При 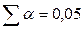 (для двустороннего критерия) и числе степеней свободы 13 табличное значение tb= 2,16. Так как фактическое значение t‑критерия превышает табличное, то, следовательно, гипотезу о несущественности коэффициента регрессии можно отклонить.
(для двустороннего критерия) и числе степеней свободы 13 табличное значение tb= 2,16. Так как фактическое значение t‑критерия превышает табличное, то, следовательно, гипотезу о несущественности коэффициента регрессии можно отклонить.
Для расчета доверительных интервалов для параметров a и b уравнения линейной регрессии определяем предельную ошибку ∆ для каждого показателя:
∆а = tтабл · ma, ∆b = tтабл · mb.
Формулы для расчета доверительных интервалов имеют вид:
γa = a ± ∆а γamin = a - ∆а γamin = a + ∆а
γb = b ± ∆b γbmin = b - ∆b γbmin = b + ∆b
Если границы интервала имеют разные знаки, т.е. в эти границы попадает ноль, то оцениваемый параметр принимается нулевым.
Доверительный интервал для коэффициента регрессии определяется как 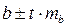 . Для коэффициента регрессии b в примере 95%-ные границы составят:
. Для коэффициента регрессии b в примере 95%-ные границы составят:
0,022 ± 2,16·0,0026 = 0,022 ± 0,0057, т.е.
0,016 ≤ b ≤ 0,027.
Поскольку коэффициент регрессии в эконометрических исследованиях имеет четкую экономическую интерпретацию, то доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, -10 ≤ b ≤ 40. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
Стандартная ошибка параметра а определяется по формуле:
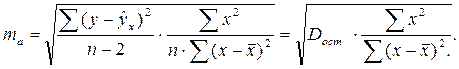
Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии; вычисляется t-критерий: 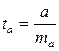 , его величина сравнивается с табличным значением при df = n - 2 степенях свободы. В нашем примере ma составила 0,032.
, его величина сравнивается с табличным значением при df = n - 2 степенях свободы. В нашем примере ma составила 0,032.
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции mr:
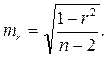
Фактическое значение t-критерия Стьюдента определяется как
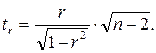
Данная формула свидетельствует, что в парной линейной регрессии 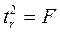 , ибо, как уже указывалось,
, ибо, как уже указывалось, 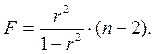 Кроме того,
Кроме того, 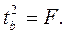 Следовательно,
Следовательно, 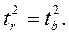
Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
В рассматриваемом примере t r совпало с tb. Величина tr =8,37 значительно превышает табличное значение 2,16 при а=0,05. Следовательно, коэффициент корреляции существенно отличен от нуля и зависимость является достоверной.
Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения фактора, называют точечным прогнозом. Вероятность точной реализации такого прогноза крайне мала. Необходимо сопроводить его значением средней ошибки прогноза или доверительным интервалом прогноза с достаточно большой вероятностью.
Точечный прогноз заключается в получении прогнозного значения yp, которое определяется путем подстановки в уравнение регрессии
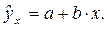 соответствующего прогнозного значения xp:
соответствующего прогнозного значения xp:
yp = a +b·xp.
Интервальный прогноз заключается в построении доверительного интервала прогноза, т.е. верхней и нижней границы ypmin, ypmax интервала, содержащего точную величину для прогнозного значения 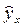
(ypmin < yp < ypmax ). Доверительный интервал всегда определяется с заданной вероятностью, соответствующей принятому значению уровня значимости α.
Предварительно вычисляется стандартная ошибка прогноза 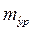 .
.

И затем строится доверительный интервал прогноза, т.е. определяется нижняя и верхняя границы интервала прогноза
 ,
, 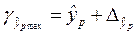 ,
,
где 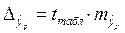 .
.
Предположим, в нашем примере необходимо найти прогнозное значение результата, при условии, что прогнозное значение фактора х увеличится на 15% от своего среднего уровня и определить доверительный интервал прогноза.
Увеличение прогнозного значения фактора х даст величину
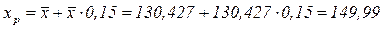 .
.
Подставляя ее в формулу, находим
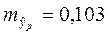 ,
,
прогнозное значение результата при заданном условии
yp = a+b∙xp = 6,63+0,022∙149,99 = 9,95.
Далее найдем нижнюю и верхнюю границы интервала, учитывая, что ранее нами определенное tтабл=2,16:
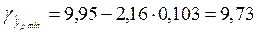 ,
,
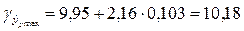 .
.
Т.о. доверительный интервал прогноза составит
9,73 < yp <10,18.
В случае нелинейной регрессии оценка существенности индекса корреляции проводится, так же как и оценка надежности коэффициента корреляции. Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера:
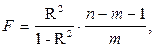
где R2 – индекс детерминации;
n – число наблюдений;
m – число параметров при переменных х.
Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n – m - 1) – число степеней свободы для остаточной суммы квадратов.
Для степенной функции 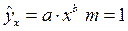 и формула F – критерия примет тот же вид, что и при линейной зависимости:
и формула F – критерия примет тот же вид, что и при линейной зависимости:
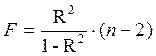
Для параболы второй степени y=a + b·x + c·x2 + ε m=2 и 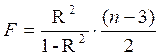 .
.
Для оценки качества построенной модели используется также средняя ошибка аппроксимации. Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е. у и 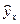 . Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у -
. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у - 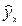 ) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует объему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Для сравнения берутся величины отклонений, выраженные в процентах к фактическим значениям. Так, если для первого наблюдения у=20, а для второго у=50, ошибка аппроксимации составит 25% для первого наблюдения и 20% - для второго.
) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует объему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Для сравнения берутся величины отклонений, выраженные в процентах к фактическим значениям. Так, если для первого наблюдения у=20, а для второго у=50, ошибка аппроксимации составит 25% для первого наблюдения и 20% - для второго.
Поскольку (у - 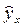 ) может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
) может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую:
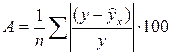 .
.
Для нашего примера представим расчет средней ошибки аппроксимации в таблице 4.
Date: 2015-07-27; view: 17273; Нарушение авторских прав