Теоретический аспект построения модели

Построение модели парной регрессии

Теоретический аспект построения модели

Для изучения различных экономических явлений специалисты используют их упрощенные формальные описания, которые называют экономическими моделями. В качестве примеров экономических моделей можно привести модели потребительского выбора, модели фирмы, модели экономического роста, модели прогнозирования какого-либо экономического явления.

Процесс эконометрического моделирования можно разбить на несколько этапов:

· Определение целей исследования данной предметной области;

· Выделение элементов модели, рассмотрение их основных характеристик;

· Описание взаимосвязей между элементами модели;

· Выбор общего вида модели, собственно, моделирование;

· Сбор необходимой статистической информации;

· Проведение необходимых расчетов и статистического анализа построенной модели на основе имеющихся данных, проверка адекватности модели.

Методы и модели регрессионного анализа занимают центральное место в математическом аппарате эконометрики. С их помощью можно установить формы зависимости между переменными, произвести оценку функции регрессии, прогнозировать значения зависимой переменной.

В зависимости от числа факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.

Простая регрессия представляет собой регрессию между двумя переменными – y и x, т.е. модель вида:

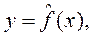
где y – зависимая переменная (результативный признак);

x – независимая переменная, или объясняющая, переменная (признак-фактор).

Множественная регрессия соответственно представляет собой регрессию результативного признака с двумя и большим числом факторов, т.е. модель вида:

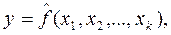
В этой главе мы рассмотрим модель парной регрессии. Простейший случай этой модели – линейная зависимость результативного признака от признака-фактора.

Общий вид такой зависимости:

y=a + b· x+ ε.

Кроме этого, существует множество математических функций, позволяющих описать связь двух переменных, например:

· Полиномиальные функции различных степеней

y = a + b·x + c·x² + d·x³ +ε;

· Гипербола ;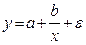

· Степенная функция y = a·x^b· ε;

· Показательная y = a·b^x· ε;

· Экспоненциальная y = e^a+bx· ε;

Эти функции относят к так называемым нелинейным регрессиям.

Как правило, модели, построенные с помощью нелинейных функций, являются более сложными, чем линейные регрессионные модели. Но в большинстве случаев, путем линеаризации нелинейную регрессионную модель можно преобразовать в линейную форму. Этим и объясняется большое внимание, уделяемое линейным свя­зям, в том числе и в нашем пособии.

Любое исследование начинается с теории, устанавливающей связь между явлениями: из множества факторов, влияющих на результативный признак, выбираются наиболее существенно влияющие факторы. В случае парной регрессии в качестве объясняющей переменной используется один фактор.

При этом нужно иметь в виду, что величина y представляет собой сумму двух слагаемых:

,

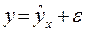где y - фактическое значение результативного признака;

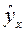- теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связи у и х, т.е. из уравнения регрессии;

ε - случайная величина (возмущение), характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.

Чем объяснить наличие случайной величины? Выделяется несколько причин:

· невключение объясняющих переменных. Соотношение между у и х почти на­верняка является очень большим упрощением. В действительности существуют другие факторы, влияющие на у, которые не учтены в формуле. Часто происходит так, что имеются переменные, которые мы хотели бы включить в регрессионное уравнение, но не можем этого сделать потому, что не знаем, как их измерить, например психологические факторы. Возможно, что существуют также другие факторы, которые мы можем измерить, но которые оказывают такое слабое влияние, что их не стоит учитывать. Кроме того, могут быть факторы, которые являются существенными, но которые мы из-за отсутствия опыта таковыми не считаем. Объединив все эти составляю­щие, мы получаем то, что обозначено как ε. Если бы мы точно знали, какие переменные присутствуют здесь, и имели возможность точно их измерить, то могли бы включить их в уравнение и исключить соответствующий элемент из случайного члена. Проблема состоит в том, что мы никогда не можем быть уверены, что входит в данную совокупность, а что — нет.

· Агрегирование переменных. Во многих случаях рассматриваемая зависи­мость — это попытка объединить вместе некоторое число микроэкономических соотношений. Например, функция суммарного потребления - это попытка общего выражения совокупности решений отдельных индивидов о рас­ходах. Так как отдельные соотношения, вероятно, имеют разные параметры, любая попытка определить соотношение между совокупными расходами и доходом является лишь аппроксимацией. Наблюдаемое расхождение при этом приписывается наличию случайного члена.

· Неправильное описание структуры модели. Структура модели может быть описана неправильно или не вполне правильно. Здесь можно привести один из многих возможных примеров. Если зависимость относится к данным о времен­ном ряде, то значение у может зависеть не от фактического значения х, а от значения, которое ожидалось в предыдущем периоде. Если ожидаемое и факти­ческое значения тесно связаны, то будет казаться, что между у и х существует зависимость, но это будет лишь аппроксимация, и расхождение вновь будет связано с наличием случайного члена.

· Неправильная функциональная спецификация. Функциональное соотношение между у и х математически может быть определено неправильно. Например, истинная зависимость может не являться линейной, а быть более сложной. Безусловно, надо постараться
избежать возникновения этой проблемы, используя подходящую математичес­кую формулу, но любая самая изощренная формула является лишь приближением, и существующее расхождение вносит вклад в остаточный член.

· Ошибки измерения. Если в измерении одной или более взаимосвязанных переменных имеются ошибки, то наблюдаемые значения не будут соответствовать точному соотношению, и существующее расхождение будет влиять на величину остаточного члена.

Остаточный член является суммарным проявлением всех этих факторов. Оче­видно, что если бы вас интересовало только измерение влияния х на у, то было бы значительно удобнее, если бы остаточного члена не было. Если бы он отсут­ствовал, мы бы знали, что любое изменение у от наблюдения к наблюдению вызвано изменением х, и смогли бы точно вычислить b. Однако в действи­тельности каждое изменение у отчасти вызвано изменением ε, и это значи­тельно усложняет жизнь.

Date: 2015-07-27; view: 754; Нарушение авторских прав