Коэффициент корреляции

Простейшей системой корреляционной связи, как мы уже сказали, является линейная связь между двумя признаками - парная линейная корреляция.

Тесноту парной линейной корреляционной связи при линейной форме уравнения измеряет коэффициент корреляции r_xy. Этот показатель представляет собой стандартизованный коэффициент регрессии, т. е. коэффициент, выраженный не в абсолютных еди­ницах измерения признаков, а в долях среднего квадратического от­клонения результативного признака:

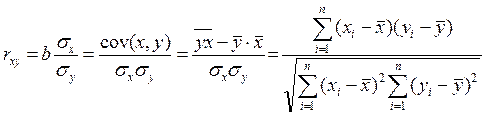
Коэффициент корреляции был предложен английским статисти­ком и философом Карлом Пирсоном (1857 – 1936 гг.). Его интерпре­тация такова: отклонение признака-фактора от его среднего значе­ния на величину своего среднего квадратического отклонения в среднем по совокупности приводит к отклонению признака-резуль­тата от своего среднего значения на r_xy его среднего квадратическо­го отклонения.

В отличие от коэффициента регрессии b коэффициент корреля­ции не зависит от принятых единиц измерения признаков, а стало быть, он сравним для любых признаков.

Выборочный коэффициент корреляции r_xy (при достаточно большом объеме выборки n) обладает следующими свойствами:

1. Коэффициент корреляции принимает значения на отрезке [-1,1], т. е.
-1 < r_xy <1. Чем ближе |r_xy| к единице, тем теснее связь.

2. При r_xy = ±1 корреляционная связь представляет линейную
функциональную зависимость. При этом все наблюдаемые значения
располагаются на прямой линии.

3. При r_xy = 0 линейная корреляционная связь отсутствует. При
этом линия регрессии параллельна оси Ох.

Причем, если r_xy > 0, то корреляционная связь между перемен­ными называется прямой, если r_xy < 0, — обратной. При прямой (обратной) связи увеличение одной из переменных ведет к увеличению (уменьшению) условной (групповой) средней другой.

Обычно считают связь сильной, если r_xy >= 0,7; средней тесноты, при 0,5 <= r_xy < 0,7; слабой при r_xy < 0,5. Не следует, особенно работая с ЭВМ, гнаться за большим числом знаков коэффициента корреля­ции. Во-первых, исходная информация редко имеет более трех зна­чащих точных цифр, во-вторых, оценка тесноты связи не требует более двух значащих цифр.

Квадрат коэффициента корреляции в случае парной линейной регрессионной модели называется коэффициентом детерминации:

.

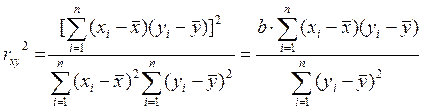Поскольку 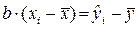, имеем

.

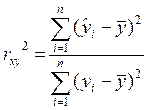Коэффициент детерминации является одной из эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии и характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака.

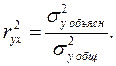
Величина 1– r²_xy характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.

Вычислим, используя приведенные выше формулы, коэффициент корреляции r_{x y} в нашем примере:

r_xy = 0,9184,
т.е. связь между показателями прямая и достаточно тесная.

Коэффициент детерминации r²_xy= 0,844, это означает, что вариация зависимой переменной y на 84% объясняется изменчивостью переменной x, на долю же прочих факторов приходится 16% дисперсии результативного признака.

Date: 2015-07-27; view: 938; Нарушение авторских прав