
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Линейная модель парной регрессии. Определение параметров
|
|
Напомним, что построение линейной регрессии сводится к нахождению уравнения вида y=a + b· x+ ε или 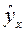 = a + b· x и оценке его параметров.
= a + b· x и оценке его параметров.
Оценить параметры линейной регрессии можно различными методами. Рассмотрим метод оценки, основанный на построении поля корреляции.
Возьмем в качестве примера зависимость между индексом реальных денежных доходов (Х) и коэффициентом рождаемости (Y) в период с 1993 по 2007 г.
| Года | Коэффициент рождаемости | Индекс реальных денежных доходов |
| y | x | |
| 9,4 | ||
| 9,6 | 131,1 | |
| 9,3 | 111,4 | |
| 8,9 | 112,5 | |
| 8,6 | 119,1 | |
| 8,8 | 100,1 | |
| 8,3 | 87,8 | |
| 8,7 | 98,4 | |
| 106,9 | ||
| 9,7 | 118,8 | |
| 10,2 | 136,6 | |
| 10,4 | 150,8 | |
| 10,2 | 167,5 | |
| 10,4 | 189,8 | |
| 11,3 | 209,6 |
Таблица 1
 Изобразим полученную зависимость графически на координатной плоскости точками (xi, yi). Такое изображение статистической зависимости называется полем корреляции. Судя по графику, можно предполагать о наличии линейной корреляционной зависимости между переменными X и Y. Далее, для оценки параметров выбираем две точки на графике и проводим через них прямую линию. Параметр а определяем как точку пересечения линии регрессии с осью OY, параметр b вычисляется как отношение приращения результата y к приращению фактора x: dy/dx.
Изобразим полученную зависимость графически на координатной плоскости точками (xi, yi). Такое изображение статистической зависимости называется полем корреляции. Судя по графику, можно предполагать о наличии линейной корреляционной зависимости между переменными X и Y. Далее, для оценки параметров выбираем две точки на графике и проводим через них прямую линию. Параметр а определяем как точку пересечения линии регрессии с осью OY, параметр b вычисляется как отношение приращения результата y к приращению фактора x: dy/dx.
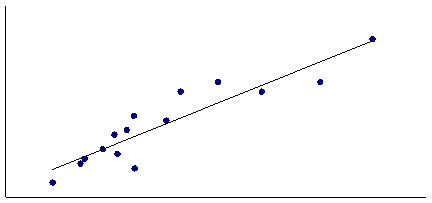
Рисунок 1
И все-таки более часто используемый метод оценивания параметров основан на методе наименьших квадратов. Согласно ему, параметры а и b выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений yi от фактических значений y, найденных по уравнению регрессии 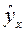 = a + b· x, была минимальной:
= a + b· x, была минимальной:
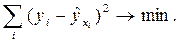
Таким образом, параметры а и b находим из системы нормальных уравнений
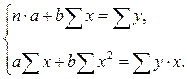
Можно также использовать готовые формулы:
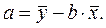
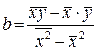 .
.
Учитывая, что cov(x,y)= 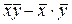 =
= 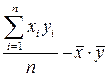 , получим
, получим
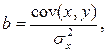
где 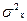 - дисперсия признака x:
- дисперсия признака x:
 ,
,
а cov(x,y)- выборочная ковариация.
Эти формулы соответствуют самому общему подходу к определению параметров уравнения регрессии и могут применяться в случае как парной, так и множественной регрессии.
Коэффициент парной линейной регрессии, обозначенный b, имеет смысл показателя силы связи между вариацией факторного признака х и вариацией результативного признака у. Он измеряет среднее по совокупности отклонение от его средней величины при отклонении признака х от своей средней величины на принятую единицу измерения.
Параметр а может не иметь экономического содержания. Интерпретировать можно лишь знак при параметре а. Если а>0, то относительное изменение результата происходит медленнее, чем изменение фактора. Иными словами, вариация результата меньше вариации фактора – коэффициент вариации по фактору х выше коэффициента вариации для результата у: Vx > Vy.
Вернемся к нашему примеру и найдем расчетным путем параметры уравнения регрессии. Для этого составим вспомогательную таблицу:
| Год | Индекс реальных денежных доходов (x) | Коэффициент рождаемости (y) | y∙x | x2 | y2 | 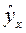
|
| 9,4 | 1090,4 | 88,36 | 9,1972 | |||
| 131,1 | 9,6 | 1258,56 | 17187,21 | 92,16 | 9,53091 | |
| 111,4 | 9,3 | 1036,02 | 12409,96 | 86,49 | 9,09554 | |
| 112,5 | 8,9 | 1001,25 | 12656,25 | 79,21 | 9,11985 | |
| 119,1 | 8,6 | 1024,26 | 14184,81 | 73,96 | 9,26571 | |
| 100,1 | 8,8 | 880,88 | 10020,01 | 77,44 | 8,84581 | |
| 87,8 | 8,3 | 728,74 | 7708,84 | 68,89 | 8,57398 | |
| 98,4 | 8,7 | 856,08 | 9682,56 | 75,69 | 8,80824 | |
| 106,9 | 962,1 | 11427,61 | 8,99609 | |||
| 118,8 | 9,7 | 1152,36 | 14113,44 | 94,09 | 9,25908 | |
| 136,6 | 10,2 | 1393,32 | 18659,56 | 104,04 | 9,65246 | |
| 150,8 | 10,4 | 1568,32 | 22740,64 | 108,16 | 9,96628 | |
| 167,5 | 10,2 | 1708,5 | 28056,25 | 104,04 | 10,33535 | |
| 189,8 | 10,4 | 1973,92 | 36024,04 | 108,16 | 10,82818 | |
| 209,6 | 11,3 | 2368,48 | 43932,16 | 127,69 | 11,26576 | |
| Итого | 1956,4 | 142,8 | 19003,19 | 272259,3 | 1369,38 | 9,1972 |
Таблица 2
 Система нормальных уравнений будет иметь вид
Система нормальных уравнений будет иметь вид
15·a+1956,4·b=142,8·y,
1956,4·a+272259,3·b=19003,19.
Решая ее, получим:
a = 6,6336,
b = 0,0221.
Уравнение регрессии будет иметь вид:
y = 0,0221·x + 6,6336.
Date: 2015-07-27; view: 1019; Нарушение авторских прав