Оценка значимости уравнения регрессии

Оценка значимости уравнения регрессии в целом проводится с помощью F-критерия Фишера. В этом случае мы выдвигаем нулевая гипотеза, что коэффициент регрессии равен нулю, т.е. b =0, и, следовательно, фактор х не оказывает влияния на результат у.

Для расчета F-критерия проведем анализ дисперсии: разложение общей суммы квадратов отклонений переменной у от среднего значения 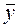на две части – «объясненную» и «необъясненную»:

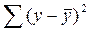
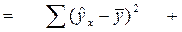
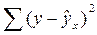
Общая сумма квадратов отклонений	Сумма квадратов отклонений, объясненная регрессией	Остаточная сумма квадратов отклонений

Общая сумма квадратов отклонений индивидуальных значений результативного признака y от среднего значения 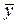вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси ОХ и 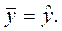Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадает с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.

Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный влиянием фактора х, т.е. регрессией y по х, так и вызванный действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результат у. Это равносильно тому, что коэффициент детерминации 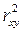будет приближаться к единице.

Любая сумма квадратов отклонений связана с числом степеней свободы (df), т.е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. При заданном наборе переменных у и х расчетное значение 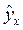является в линейной регрессии функцией только одного параметра – коэффициента регрессии. Соответственно и факторная сумма квадратов отклонений имеет число степеней свободы, равное 1.

Существует равенство между числом степеней свободы, факторной и остаточной суммами квадратов. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет n - 2. Число степеней свободы для общей суммы квадратов определяется числом единиц, и поскольку мы используем среднюю вычисленную по данным выборки, то теряем одну степень свободы, т.е. df_общ= n - 1.

Т.о. можно определить средний квадрат отклонений, или, что то же самое, дисперсию на одну степень свободы D:

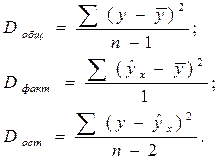
Откуда получим величину F-отношения (F-критерий):

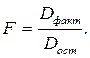
где F – критерий для проверки нулевой гипотезы Н₀: D_факт= D_ост.

Вывод о справедливости нулевой гипотезы можно сделать из сравнения табличного и факторного значения F-критерия. Английским статистиком Снедекором разработаны таблицы критических значений F‑отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: если F_факт>F_табл, то Н₀ отклоняется.

Если же величина окажется меньше табличной F_факт<F_табл, то вероятность нулевой гипотезы выше заданного уровня (например, 0,05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается незначимым, Н₀ не отклоняется.

Исходя из того, что величина F-критерия связана с коэффициентом детерминации, формулу F-критерия можно записать и так:

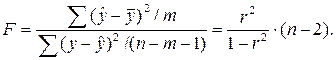
Применительно к нашему примеру

,

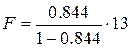F= 70,07.

Такое же значение получаем по формуле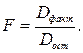

D_факт= 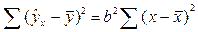= 0,022²·(272259,3 - 15·(1956,4:15)²) = 8,371.

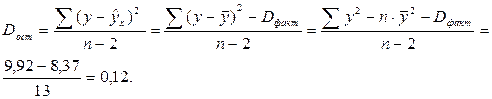
F_факт = 8,371:0,12 = 70,07.

F_табл находим из таблицы (см. Приложение 1):

F_табл=4,67 (по таблице k₁= 1, k₂= n – m - 1 = 13).

Как видим, F_табл<F_факт, т.е. можно сделать вывод о статистической значимости параметров данного уравнения (связь доказана).

Оценка значимости уравнения регрессии представима в виде
Схемы дисперсионного анализа:

Компоненты дисперсии (источник вариации)	Сумма квадратов отклонений	Число степеней свободы	Дисперсия на одну степень свободы
Факторная (регрессия)		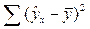m-1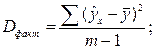
Остаточная		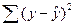n-m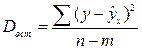
Общая		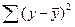n-1	-

Таблица 3

 

В нашем примере она будет выглядеть следующим образом:

Компоненты дисперсии (источник вариации)	Сумма квадратов отклонений	Число степеней свободы	Дисперсия на одну степень свободы
Регрессия	8,371	1	8.371
Остаточная	1,553	13	0,11948
Общая	9,924	14

Date: 2015-07-27; view: 2047; Нарушение авторских прав