Раздел IV. Механические колебания и волны

· Уравнение гармонических колебаний

,

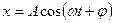где х – смещение колеблющейся точки от положения равновесия; t – время; A, ω, φ – соответственно амплитуда, циклическая частота, начальная фаза колебаний; 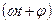– фаза колебаний в момент t.

· Циклическая частота колебаний

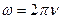, или ,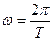

где ν и Т – частота и период колебаний. Единица измерения частоты герц (Гц).

· Скорость точки, совершающей гармонические колебания

.

· Ускорение при гармоническом колебании

.

· Амплитуда результирующего, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле

,

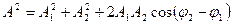где А ₁ и А ₂ – амплитуды составляющих колебаний, м; φ ₁ и φ ₂ – их начальные фазы.

· Начальная фаза результирующего колебания

.

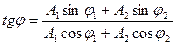· Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по значению частотами ν ₁ и ν ₂

.

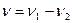· Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты с амплитудами А ₁ и А ₂ и начальными фазами φ ₁ и φ ₂

.

Если начальные фазы φ ₁ и φ ₂ составляющих колебаний одинаковы, то уравнение траектории примет вид

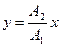или ,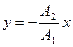

т.е. точка движется по прямой.

В том случае, если разность фаз 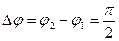, уравнение принимает вид

,

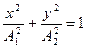т.е. точка движется по эллипсу.

· Дифференциальное уравнение гармонических колебаний материальной точки

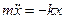или ,

где m – масса точки; k – коэффициент квазиупругой силы (k = mω²).

· Полная энергия материальной точки, совершающей гармонические колебания

.

· Период колебаний тела, подвешенного на пружине (пружинный маятник)

,

где m – масса тела; k – жесткость пружины. Единица измерения периода секунда (с).

Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).

· Период колебаний математического маятника

,

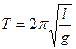где l – длина маятника; g – ускорение свободного падения.

· Период колебаний физического маятника

,

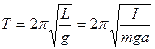где I – момент инерции колеблющегося тела относительно оси колебаний; а – расстояние центра масс маятника от оси колебаний; L = 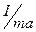– приведенная длина физического маятника.

· Дифференциальное уравнение затухающих колебаний

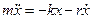, или ,

где r – коэффициент сопротивления; δ – коэффициент затухания: 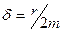; ω₀ – собственная циклическая частота колебаний: .

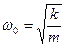· Уравнение затухающих колебаний

,

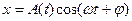где A (t) – амплитуда затухающих колебаний в момент t; ω – их циклическая частота.

· Циклическая частота затухающих колебаний

.

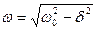· Зависимость амплитуда затухающих колебаний от времени

,

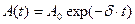где А ₀ – амплитуда колебаний в момент t = 0.

· Логарифмический декремент затухания

,

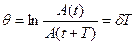где A (t) и A (t + T) – амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период.

· Дифференциальное уравнение вынужденных колебаний

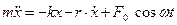или ,

где F ₀ cosωt – внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания; F ₀ – ее амплитудное значение; .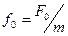

· Амплитуда вынужденных колебаний

.

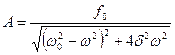· Резонансная частота и резонансная амплитуда

и .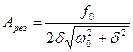

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Частица массой m = 0,01 кг совершает гармонические колебания с периодом Т = 2 с. Полная энергия колеблющейся частицы Е = 0,1 мДж. Определить амплитуду колебаний и наибольшее значение силы, действующей на частицу.

Решение: Для определения амплитуды колебаний воспользуемся выражением полной энергии частицы:

, где .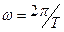

Отсюда амплитуда

. (1)

Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением F = - kx, где k – коэффициент квазиупругой силы; х – смещение колеблющейся точки. Максимальной сила будет при максимальном смещении x _max, равном амплитуде:

F _max = kA. (2)

Коэффициент k выразим через период колебаний:

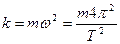. (3)

Подставив выражения (1) и (3) в (2) и произведя упрощения, получим:

.

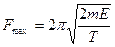Произведем вычисления:

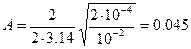м.

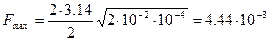Н.

Пример 2. Плоская волна распространяется вдоль прямой со скоростью 20 м/с. Две точки, находящиеся на этой прямой на расстоянии х ₁ = 12 см и х ₂ = 15 м от источника волн, колеблются с разностью фаз ∆ φ = 0,75π. Найти длину волны, написать уравнение волны и найти смещение указанных точек в момент t =1,2 с, если амплитуда колебаний 0,1 м.

Решение: Точки, находящиеся друг от друга на расстоянии, равном длине волны, колеблются с разностью фаз, равной 2π; точки, находящиеся друг от друга на любом расстоянии ∆ х, колеблются с разностью фаз, равной

.

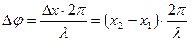Решая это равенство относительно λ, получаем

м. (1)

Для того, чтобы написать уравнение плоской волны, надо еще найти циклическую частоту ω. Так как 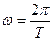(Т = λ / υ – период колебаний), то

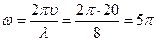с^-1.

Зная амплитуду колебаний, циклическую частоту и скорость распространения волны, можно написать уравнение плоской волны для данного случая:

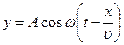, (2)

где А = 0,1 м, ω = 5π с^-1, υ = 20 м/с.

Чтобы найти смещение y указанных точек, достаточно в уравнение (2) подставить значения t и х:

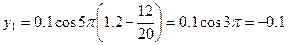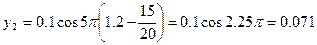м.

м.

Пример 3. Физический маятник представляет собой стержень длиной l = 1 м и массой 3 m ₁ с прикрепленным к одному из его концов обручем диаметром d = l /2 и массой m ₁. Горизонтальная ось Oz маятника проходит через середину стержня перпендикулярно ему (рис. 45). Определить период колебаний такого маятника.

Решение: Период колебаний физического маятника определяется по формуле: 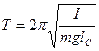, (1) где I – момент инерции маятника относительно оси колебаний; m – его масса; l C – расстояние от центра масс маятника до оси колебаний. Момент инерции маятника равен сумме моментов инерции стержня I 1 и обруча I 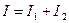2: . (2)

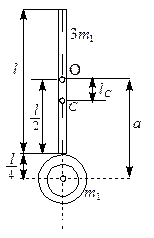Рис. 45. Физический маятник

Момент инерции стержня относительно оси, перпендикулярной стержню и проходящей через его центр масс, определяется по формуле 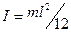. В данном случае m = 3 m ₁ и .

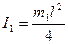Момент инерции обруча найдем, воспользовавшись теоремой Штейнера: 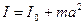, где I – момент инерции относительно произвольной оси; I ₀ – момент инерции относительно оси, проходящей через центр масс параллельно заданной оси; а – расстояние между указанными осями. Применив эту формулу к обручу, получим .

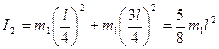Подставив выражения I ₁ и I ₂ в формулу (2), найдем момент инерции маятника относительно оси вращения:

.

Расстояние l _C от оси маятника до его центра масс равно

, или .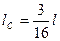

Подставив в формулу (1) выражения I, l _C и массы маятника (m = 3 m ₁ + m ₁ = 4 m ₁), найдем период его колебаний:

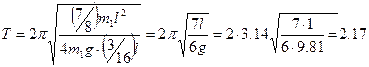с.

Date: 2015-08-15; view: 677; Нарушение авторских прав