
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Магнетизм. · Механический момент, действующий на контур с током (рис
|
|
· Механический момент, действующий на контур с током (рис. 32), помещенный в однородное магнитное поле
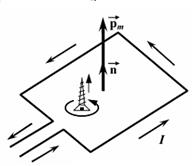 Рис. 32. Рамка с током
Рис. 32. Рамка с током
|
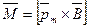 ,
где ,
где 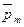 - вектор магнитного момента рамки с током; - вектор магнитного момента рамки с током; 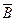 - вектор магнитной индукции (количественная характеристика магнитного поля). Единица измерения магнитной индукции тесла (Тл). - вектор магнитной индукции (количественная характеристика магнитного поля). Единица измерения магнитной индукции тесла (Тл).
|
· Закон Био-Савара-Лапласа: каждый элемент 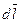 проводника с током создает в некоторой точке А индукцию поля
проводника с током создает в некоторой точке А индукцию поля 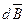 (рис. 33)
(рис. 33)
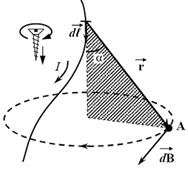 Рис. 33. Магнитное поле, созданное проводником с током
Рис. 33. Магнитное поле, созданное проводником с током
| 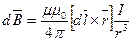 ,
где ,
где 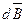 – магнитная индукция поля, создаваемого элементом проводника с током, Тл; μ – магнитная проницаемость; μ 0 – магнитная постоянная (μ0 = 4π·10-7 Гн/м); – магнитная индукция поля, создаваемого элементом проводника с током, Тл; μ – магнитная проницаемость; μ 0 – магнитная постоянная (μ0 = 4π·10-7 Гн/м); 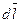 – вектор, равный по модулю длине d l проводника и совпадающий по направлению с током; I – сила тока; – вектор, равный по модулю длине d l проводника и совпадающий по направлению с током; I – сила тока; 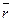 – радиус вектор, проведенный от середины элемента проводника к точке, магнитная индукция в которой определяется. – радиус вектор, проведенный от середины элемента проводника к точке, магнитная индукция в которой определяется.
|
· Модуль вектора 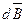 выражается формулой
выражается формулой
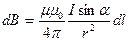 ,
,
где α – угол между векторами 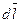 и
и 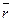 .
.
· Магнитная индукция 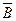 связана с напряженностью
связана с напряженностью 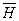 магнитного поля соотношением
магнитного поля соотношением 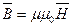 .
.
· Магнитная индукция в центре кругового проводника с током (рис. 34)
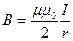 ,
,
где r – радиус витка.
· Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током (рис. 35)
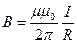 ,
,
где R – расстояние от оси проводника.
· Магнитная индукция поля, создаваемая соленоидом в средней его части (рис. 36)
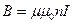 ,
,
где n – число витков, приходящихся на единицу длины соленоида; I – сила тока в одном витке.
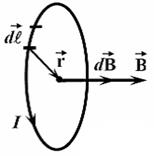 Рис. 34. Магнитное поле, созданное круговым проводником с током
Рис. 34. Магнитное поле, созданное круговым проводником с током
| 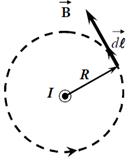 Рис. 35. Магнитное поле, созданное длинным прямым проводником с током
Рис. 35. Магнитное поле, созданное длинным прямым проводником с током
| 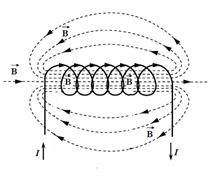 Рис. 36. Магнитное поле, созданное соленоидом
Рис. 36. Магнитное поле, созданное соленоидом
|
· Принцип суперпозиции магнитных полей: магнитная индукция результирующего поля равна векторной сумме магнитных индукций складываемых полей 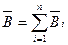 .
.
В частном случае наложения двух полей
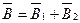 ,
,
а модуль магнитной индукции
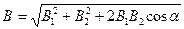 ,
,
где α – угол между векторами 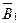 и
и 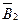 .
.
· Магнитная индукция поля, создаваемого движущимся точечным зарядом в вакууме
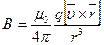 , или
, или 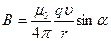 ,
,
где 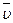 - скорость движущегося заряда;
- скорость движущегося заряда; 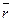 - радиус-вектор, направленный от заряда к точке, в которой определяется магнитная индукция; α – угол между векторами
- радиус-вектор, направленный от заряда к точке, в которой определяется магнитная индукция; α – угол между векторами 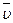 и
и 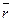 .
.
· Закон Ампера
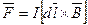 ,
,
где 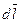 - вектор, по модулю равный d l и совпадающий по направлению с током;
- вектор, по модулю равный d l и совпадающий по направлению с током; 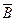 - вектор магнитной индукции.
- вектор магнитной индукции.
Модуль силы Ампера вычисляется по формуле
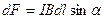 ,
,
где α – угол между векторами 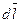 и
и 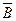 .
.
В случае однородного магнитного поля и прямолинейного отрезка проводника 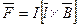 , или
, или 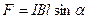 .
.
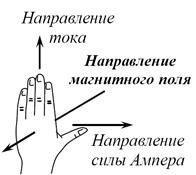 Рис. 37. Правило левой руки
Рис. 37. Правило левой руки
| Направление вектора может быть найдено, согласно последней формуле, по общим правилам векторного произведения. Этим правилам соответствует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток (рис. 37). |
· Магнитный момент контура с током
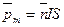 ,
,
где 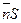 - вектор, равный по модулю площади, охватываемой контуром, и совпадающий по направлению с нормалью
- вектор, равный по модулю площади, охватываемой контуром, и совпадающий по направлению с нормалью 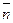 к его плоскости.
к его плоскости.
· Сила Лоренца – сила действующая на одну заряженную частицу, движущуюся в магнитном поле.
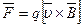 , или
, или 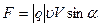 ,
,
где α – угол, образованный вектором скорости движущейся частицы и вектором магнитной индукции (рис. 37).
· Магнитный поток Ф через плоский контур площадью S (рис. 38)
а) в случае однородного поля
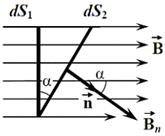 Рис. 38. Магнитный поток через плоский контур
Рис. 38. Магнитный поток через плоский контур
|
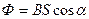 , или , или 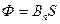 где α – угол между вектором нормали
где α – угол между вектором нормали 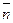 к плоскости контура и вектором магнитной индукции к плоскости контура и вектором магнитной индукции 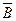 , В n – проекция вектора , В n – проекция вектора 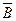 на нормаль на нормаль 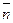 . .
|
б) в случае неоднородного поля
 ,
,
где интегрирование ведется по всей поверхности S.
· Работа сил магнитного поля, совершаемая при перемещении контура с током в магнитном поле
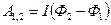 ,
,
где I – сила тока в контуре, которая поддерживается неизменной; Ф 2 и Ф 1 – магнитные потоки, пронизывающие контур, в конечном и начальном его положениях.
· Закон Фарадея-Максвелла (основной закон электромагнитной индукции)
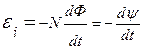 ,
,
где εi – электродвижущая сила индукции; N – число витков контура; ψ - потокосцепление.
· Электродвижущая сила самоиндукции, возникающая в замкнутом контуре при изменении силы тока в нем
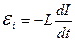 ,
,
где L – индуктивность контура.
· Энергия магнитного поля
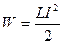 ,
,
где I – сила тока в контуре.
· Формула Томсона. Период собственных колебаний в контуре без активного сопротивления
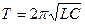 ,
,
где L – индуктивность контура, Гн; С – его электроемкость, Ф.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Мягкая спиральная пружина подвешена так, что ее нижний конец погружен в металлическую чашечку с ртутью, а верхний присоединен к источнику постоянного тока. Что произойдет с пружиной при замыкании ключа К?
Решение: При замыкании ключа К по пружине потечет ток. Каждый виток пружины будет создавать магнитное поле и притягивать к себе соседние витки (разноименные полюса магнитов притягиваются). Пружина сожмется, нижний конец пружины поднимется из ртути, цепь разомкнется, и ток перестанет идти. Если нет тока, нет и магнитного поля между витками и пружина расправится.
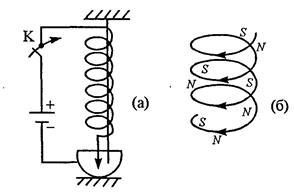
Рис. 39
После опускания нижнего конца пружины в ртуть весь процесс начнется сначала. Таким образом, пружина совершает периодические колебания.
Эту задачу можно решить и по-другому. Отдельные участки соседних витков, лежащие друг против друга, можно рассматривать как параллельные участки проводников, по которым текут токи в одном направлении (рис. 39б), такие проводники притягиваются друг к другу. Поэтому витки пружины будут притягиваться друг к другу и пружина сожмется, а нижний конец ее поднимется из ртути, разрывая цепь, по которой протекает ток. Исчезает магнитное поле проводников, и пружина вновь распрямляется. Конец пружины опускается в чашку с ртутью, вновь замыкая цепь, и т.д.
Пример 2. По длинному прямому тонкому проводу течет ток силой I = 20 А. Определить магнитную индукцию 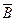 поля, создаваемого проводником в точке, удаленной от него на расстояние r = 4 см.
поля, создаваемого проводником в точке, удаленной от него на расстояние r = 4 см.
Решение: В задаче рассматривается явление создания магнитного поля проводником с током. Проведем силовую линию магнитного поля через точку А (рис. 40), в которой определяется магнитная индукция 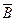 . Магнитное поле, создаваемое проводником бесконечной длины, обладает осевой симметрией. Поэтому в плоскости, проходящей через точку А и перпендикулярной проводу, проведем окружность радиуса OA = r (рис. 40).
. Магнитное поле, создаваемое проводником бесконечной длины, обладает осевой симметрией. Поэтому в плоскости, проходящей через точку А и перпендикулярной проводу, проведем окружность радиуса OA = r (рис. 40).
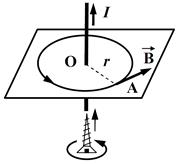 Рис. 40. Правило буравчика
Рис. 40. Правило буравчика
| Направление силовой линии и направление тока связаны правилом правого винта (буравчика): если поступательное движение винта направить по току, то вращательное движение головки винта укажет направление силовой линии (рис. 40). Определение направления силовой линии следует из закона Био-Савара-Лапласа, записанного в векторной форме: |
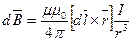 .
.
Вектор 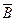 совпадает с касательной в точке А и направлен так же, как силовая линия. Запишем выражение для магнитной индукции поля бесконечно длинного проводника с током на расстоянии r от него из уравнения
совпадает с касательной в точке А и направлен так же, как силовая линия. Запишем выражение для магнитной индукции поля бесконечно длинного проводника с током на расстоянии r от него из уравнения 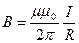 . Считая, что проводник находится в вакууме (μ = 1), вычисляем, подставляя все величины в единицах системы СИ:
. Считая, что проводник находится в вакууме (μ = 1), вычисляем, подставляя все величины в единицах системы СИ:
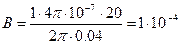 Тл.
Тл.
Пример 3. Два параллельных бесконечно длинных провода D и C, по которым текут в одном направлении электрические токи силой I 1 = I 2 = 60 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию 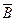 поля, создаваемого проводником с током в точке A, отстоящей от оси одного проводника на расстояние r 1 = 5 см, от другого – r 2 = 12 см.
поля, создаваемого проводником с током в точке A, отстоящей от оси одного проводника на расстояние r 1 = 5 см, от другого – r 2 = 12 см.
| Решение: В задаче рассматривается явление создания магнитного поля системой проводников. Проведем через точку A (рис. 41) часть силовой линии магнитного поля, создаваемого током I 1, а затем часть силовой линии магнитного поля, которое создается током I 2 (пунктирные дуги). | 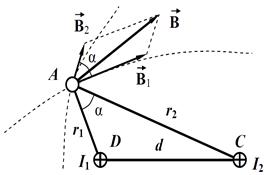 Рис. 41. Магнитное поле, созданное двумя бесконечно длинными проводниками
Рис. 41. Магнитное поле, созданное двумя бесконечно длинными проводниками
|
Построим 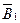 и
и 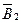 как касательные к этим дугам в точке А. Так как магнитные индукции определяются по формулам:
как касательные к этим дугам в точке А. Так как магнитные индукции определяются по формулам:
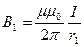 и
и 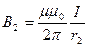 , (1)
, (1)
токи I 1 = I 2 = I, а r 1 < r 2, то B 1 > B 2.
Для нахождения в точке A магнитной индукции B, создаваемой системой проводников с токами, воспользуемся принципом суперпозиции магнитных полей. Для этого сложим 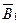 и
и 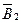 геометрически, по правилу параллелограмма:
геометрически, по правилу параллелограмма: 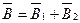 . Модуль вектора
. Модуль вектора 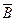 найдем по теореме косинусов:
найдем по теореме косинусов:
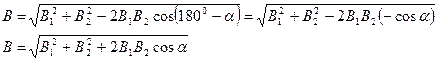 , (2)
, (2)
где α – угол между векторами 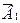 и
и 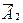 . Подставляя B 1 и B 2 (1) в формулу (2), и вынося
. Подставляя B 1 и B 2 (1) в формулу (2), и вынося 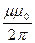 за знак корня, получаем
за знак корня, получаем
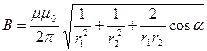 . (3)
. (3)
Найдем cos α из треугольника DAC. Заметим, что α = ∟DAC, как углы со взаимно перпендикулярными сторонами (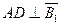 ,
, 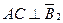 ; AD и AC – радиусы;
; AD и AC – радиусы; 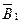 и
и 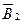 – касательные в точке A). По теореме косинусов запишем
– касательные в точке A). По теореме косинусов запишем 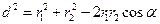 , где d = DC – расстояние между проводами.
, где d = DC – расстояние между проводами.
Отсюда 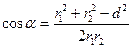 ;
; 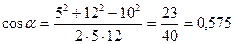 .
.
Теперь можно все данные подставить в формулу (3) и найти индукцию поля:
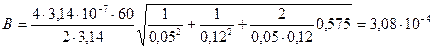 Тл или 308 мкТл.
Тл или 308 мкТл.
Пример 4. Электрон, пройдя ускоряющую разность потенциалов U = 400 В, попал в однородное магнитное поле напряженностью H = 1 кА/м. Определить радиус R кривизны траектории и частоту ν обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля 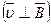 .
.
Решение: В задаче рассматривается явление силового действия магнитного поля на движущийся заряд (рис. 42). На движущийся в магнитном поле заряд действует сила Лоренца 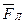 (действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение. (действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение.
| 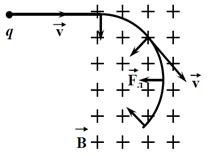 Рис. 42. Движение электрона
в однородном магнитном поле
Рис. 42. Движение электрона
в однородном магнитном поле
|
По второму закону Ньютона 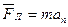 , где a n – нормальное ускорение
, где a n – нормальное ускорение
или 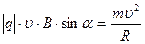 , (1)
, (1)
где | q | – модуль заряда электрона; υ – скорость электрона; В – магнитная индукция; m – масса электрона; R – радиус кривизны траектории; α – угол между векторами 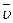 и
и 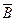 (в данном случае α = 900, sin α = 1).
(в данном случае α = 900, sin α = 1).
Из формулы (1) найдем
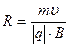 . (2)
. (2)
Входящий в это равенство импульс p = m υ может быть выражен через кинетическую энергию Е к электрона:
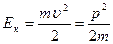 , откуда
, откуда 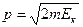 . (3)
. (3)
Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется работой электрического поля по ускорению электрона и по закону сохранения энергии Е к = А = | q |· U. Подставляя это выражение в формулу (3), получим 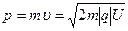 .
.
Магнитная индукция B может быть выражена через напряженность H магнитного поля в вакууме: 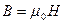 .
.
Подставив выражения для В и 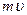 в формулу (2), получим
в формулу (2), получим
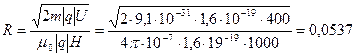 м или 5,37 см.
м или 5,37 см.
Учитывая, что частота обратно пропорциональна периоду 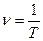 , а период можно определить как
, а период можно определить как 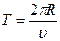 , получим формулу, связывающую частоту со скоростью и радиусом:
, получим формулу, связывающую частоту со скоростью и радиусом: 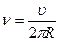 . Подставив в последнюю формулу выражение (2), получим
. Подставив в последнюю формулу выражение (2), получим
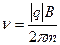 или
или 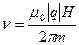 .
.
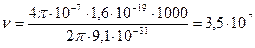 с-1.
с-1.
Пример 5. Длинный соленоид с сердечником из немагнитного материала содержит N = 1200 витков провода, плотно прилегающих друг к другу. При силе тока I = 4 А магнитный поток Ф = 6 мкВб. Определить индуктивность L соленоида и энергию W магнитного поля соленоида, объемную плотность энергии магнитного поля w, если длина соленоида l = 1 м.
Решение: В задаче рассматривается явление создания магнитного поля соленоидом с током (рис. 43). Индуктивность L связана с потокосцеплением Ψ и силой тока I соотношением 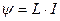 . (1)
. (1)
Потокосцепление, в свою очередь, может быть определено через поток Ф и число витков N (при условии, что витки плотно прилегают друг к другу):
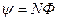 . (2)
. (2)
Из формул (1) и (2) находим индуктивность соленоида
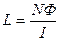 . (3)
. (3)
Энергия магнитного поля соленоида: 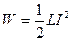 .
.
Выразив L согласно уравнению (3), получим энергию магнитного поля:
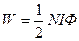 . (4)
. (4)
Подставим значения физических величин в единицах СИ в формулы (3) и (4) и вычислим значения L и W:
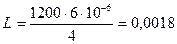 Гн или 1,8 мГн.
Гн или 1,8 мГн.
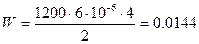 Дж или 14,4 мДж.
Дж или 14,4 мДж.
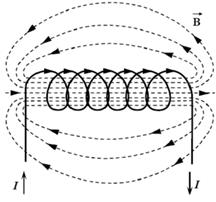 Рис. 43. Соленоид
Рис. 43. Соленоид
| Энергию магнитного поля можно найти и другим способом.
Запишем энергию магнитного поля как:
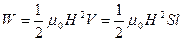 , (5)
где V, l – объем и длина соленоида, S – площадь витка.
Напряженность магнитного поля длинного соленоида (d << l) , (5)
где V, l – объем и длина соленоида, S – площадь витка.
Напряженность магнитного поля длинного соленоида (d << l)
 . (6) . (6)
|
Магнитный поток внутри соленоида равен Ф = BS cos α. В длинном соленоиде α = 0, поэтому cos α = 1.
Тогда Ф = BS cos 00 = BS = μμ0 HS = μ0 nIS,
где μ = 1 для немагнитного материала.
Из этой формулы выразим площадь S:
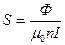 . (7)
. (7)
Подставим формулы (6) и (7) в формулу (5):
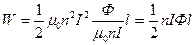 .
.
Учитывая, что 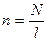 , получим формулу для вычисления энергии поля соленоида:
, получим формулу для вычисления энергии поля соленоида: 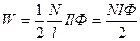 .
.
Объёмная плотность энергии магнитного поля равна
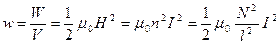 .
.
Подставляя данные, получим, 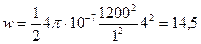 Дж/м3.
Дж/м3.
Пример 6. Электрон, ускоренный разностью потенциалов U = 6 кВ, влетает в однородное магнитное поле под углом α = 30o к направлению поля и движется по винтовой траектории. Индукция магнитного поля B = 13 мТл. Найти радиус R, шаг h винтовой траектории, период T обращения электрона, его кинетическую энергию.
Решение: В задаче рассматривается явление действия магнитного поля на движущийся в нем заряд. Разложим скорость электрона, влетающего в магнитное поле, по двум направлениям: вдоль линий поля – 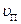 и перпендикулярно ему –
и перпендикулярно ему – 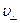 .
.
На основании закона сохранения энергии работа электрического поля А = | q | U переходит в кинетическую энергию электрона 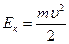 ,
,
поэтому
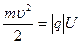 . (1)
. (1)
Из этой формулы определим скорость
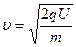 ,
, 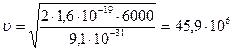 м/с.
м/с.
|
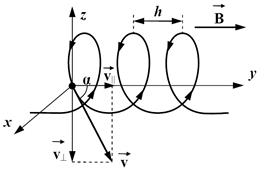
| Рис. 44. Движение электрона в однородном магнитном поле |
Из рис. 44 видно, что υ ׀׀ = υ∙ cos α, 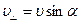 . Формула для радиуса R:
. Формула для радиуса R:
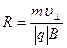 .
.
Тогда 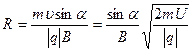 .
.
Проведя вычисления, получим
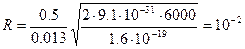 м.
м.
Шаг спирали найдем из соотношений: 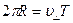 и
и 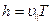 ,
,
откуда 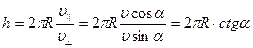 .
.
Проведя вычисления, получим 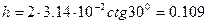 м.
м.
Тогда период обращения электрона найдем как: 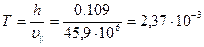 с.
с.
Date: 2015-08-15; view: 2150; Нарушение авторских прав