Электростатика в вакууме и веществе

· Закон Кулона

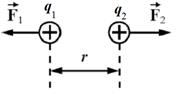Рис. 10. Взаимодействие зарядов

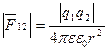, где – сила, действующая на точечный заряд q 1 со стороны точечного заряда q 2, Кл (рис.10); ε 0 = 8,85·10-12 Ф/м – электрическая постоянная; ε – диэлектрическая постоянная среды.

· Принцип суперпозиции: результирующая сила 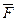, действующая на пробный заряд равна геометрической сумме сил 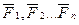(рис.11).

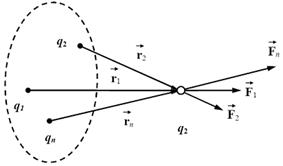Рис. 11. Система точечных зарядов

.

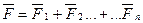· Напряженность электрического поля в точке

.

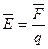Единица измерения напряженности вольт на метр (В/м).

· Принцип суперпозиции (наложения) электрических полей

.

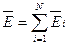В случае наложения двух электрических полей с напряженностям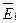и и модуль вектора напряженности определяется по теореме косинусов:

,

где α – угол между векторам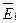и и .

· Графическое изображение электростатического поля: в наглядной форме электростатическое поле принято изображать графически с помощью линий напряженности электростатического поля (рис. 12).

На рис. 3 представлены линии напряженности поля:

а) линия напряженности (силовая линия) – линия, проведенная в электростатическом поле так, что вектор напряженности в каждой ее точке направлен по касательной к этой линии;

б) положительного точечного заряда;

в) отрицательного точечного заряда;

г) двух разноименных зарядов (диполя).

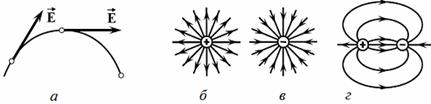
Рис. 12. Линии напряженности

· Поток вектора напряженности электрического поля

а) через произвольную поверхность S, помещенную в неоднородное поле

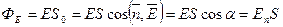
где α – угол между вектором напряженности и нормалью n к элементу поверхности; S _о – проекция площадки S на плоскость перпендикулярную силовым линиям; E _n – проекция вектора напряженности на нормаль (рис. 13).

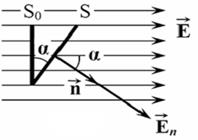Рис. 13. Поток вектора напряженности через поверхность S

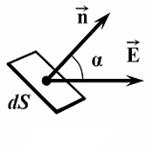Рис. 14. Поток вектора напряженности через плоскую поверхность d S

б) через плоскую поверхность (рис. 14), помещенную в однородное электрическое поле

.

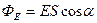Поток вектора напряженности через замкнутую поверхность

,

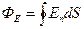где интегрирование ведется по всей поверхности.

· Напряженность электрического поля, создаваемого точечным зарядом q на расстоянии r от заряда

.

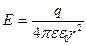· Напряженность электрического поля, создаваемого металлической сферой радиусом R, несущей заряд q, на расстоянии r от центра сферы:

а) внутри сферы (r < R)

;

б) на поверхности сферы (r = R)

;

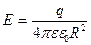в) вне сферы (r > R)

.

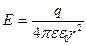· Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром, рис. 15) на расстоянии r от ее оси

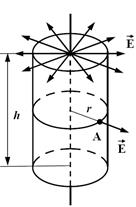Рис. 15. Бесконечно длинная равномерно заряженная нить

, где 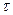– линейная плотность заряда, Кл/м.

· Линейная плотность заряда есть величина, равная отношению заряда, распределенного по нити, к длине нити:

.

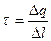· Напряженность поля, создаваемой бесконечной равномерно заряженной плоскостью (рис. 16)

Рис. 16. Равномерно заряженная плоскость

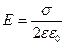где σ – поверхностная плотность заряда, Кл/м2.

· Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к площади этой поверхности:

.

· Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями с одинаковой по модулю поверхностной плотностью заряда σ (рис. 17)

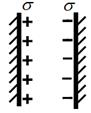Рис. 17. Поле, образованное двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями

.

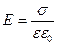· Потенциал электростатического поля

,

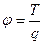где T – потенциальная энергия точечного заряда, помещенного в данную точку поля, при условии, что его потенциальная энергия в бесконечности принята равной нулю. Единица измерения потенциала вольт (В).

· Связь между потенциалом и напряженностью электростатического поля: проекция вектора напряженности электростатического поля E_l на любое направление l в пространстве равна убыли потенциала на единице длины вдоль этого направления

.

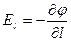· Потенциал электрического поля, создаваемый точечным зарядом q на расстоянии r от заряда .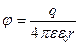

· Потенциал электрического поля, создаваемого металлической, несущей заряд q сферой радиусом R, на расстоянии r от центра сферы (рис. 18):

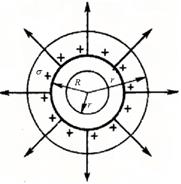Рис. 18. Равномерно заряженная металлическая сфера

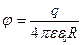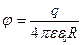а) внутри сферы (r < R) ; б) на поверхности сферы (r = R) ; в) вне сферы (r > R) .

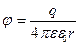· Работа, совершаемая электрическим полем при перемещении точечного заряда из одной точки поля, имеющей потенциал φ ₁, в другую, имеющую потенциал φ ₂: .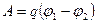

· Электрическая емкость уединенного проводника

.

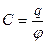Единица измерения емкости фарад (Ф).

· Электроемкость конденсатора

,

где – разность потенциалов на обкладках конденсатора.

· Электрическая емкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью ε

.

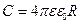· Электрическая емкость плоского конденсатора

,

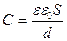где S – площадь пластин; d – расстояние между ними; ε – диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

Электрическая емкость плоского конденсатора, заполненного n слоями диэлектрика толщиной d_i каждый с диэлектрическими проницаемостями ε_i

.

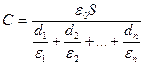· Электрическая емкость сферического конденсатора (две концентрические сферы радиусами R ₁ и R ₂, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ε)

.

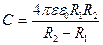· Электрическая емкость цилиндрического конденсатора (два коаксиальных цилиндра длиной l и радиусами R ₁ и R ₂, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ε)

.

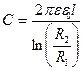· Электрическая емкость последовательно соединенных конденсаторов

в общем случае ,

где n – число конденсаторов;

в случае двух конденсаторов .

· Электрическая емкость параллельно соединенных конденсаторов

в общем случае ;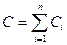

в случае двух конденсаторов .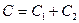

· Энергия заряженного проводника

; ; .

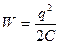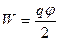· Энергия заряженного конденсатора

; ; .

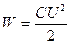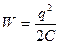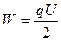ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

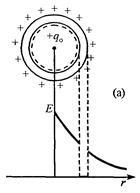
Пример 1. В центре полой проводящей незаряженной сферы помещен точечный заряд q ₀.

1) Где и какие электрические поля будут существовать?

2) Будут ли появляться заряды на сфере?

3) Будут ли происходить изменения электрического поля внутри и вне сферы при перемещении заряда внутри сферы?

4) Как будет меняться поле внутри и вне сферы, если заряд останется неподвижным, а внешнюю поверхность сферы заземлить на короткое время, а затем заряд осторожно вывести из полости сферы, не касаясь ее, через маленькое отверстие?

5) Где и какие заряды на сфере будут существовать, если точечный заряд поднести снаружи к незаряженной сфере?

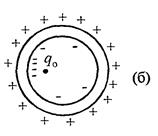
Решение: Внутри полой проводящей сферы будет существовать поле, определяемое по формуле для поля точечного заряда 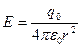. На внутренней поверхности сферы наведется заряд – q ₀, который расположен равномерно по внутренней поверхности. Так как сфера нейтральна, на ее внешней поверхности равномерно расположен заряд ₊ q ₀. Внутри металлического слоя поле равно нулю. Вне сферы поле определяется зарядом + q ₀ по формуле для поля точечного заряда рис. 19 (а)

Рис. 19

При перемещении заряда внутри сферы изменяется электрическое поле внутри сферы, изменяется распределение отрицательного заряда на внутренней поверхности сферы рис. 19 (б).

Однако распределение положительного заряда на внешней поверхности сферы, а следовательно, и поле вне сферы изменяться не будет. Это связано с тем, что поле внутри металлического слоя равно нулю, поэтому изменение поля внутри сферы не влияет на распределение зарядов на ее внешней поверхности.

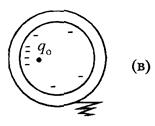
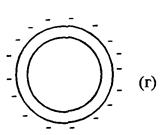
При заземлении на некоторое время внешней поверхности сферы все положительные заряды «уйдут» в землю (на самом деле из поверхности земли, которая является хорошим проводником, на внешнюю поверхность сферы придут электроны, которые компенсируют ее положительный заряд). В этом случае внутри сферы поле будет существовать, а вне ее поле равно нулю рис. 19 (в). После выведения заряда q ₀ из полости сферы отрицательные заряды начнут расталкиваться до тех пор, пока не распределяться равномерно на внешней поверхности сферы. В этом случае поле внутри сферы равно нулю, а вне сферы существует электрическое поле, подобное полю точечного заряда - q ₀, помещенного в центре сферы рис. 19 (г).

Рис. 19

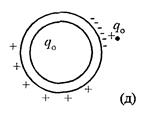
Если же заряд q ₀ поднести к сфере снаружи, то на внешней поверхности сферы образуется наведенный (индуцированный) заряд, который распределен, как показано на рис. 19 (д). Вне сферы результирующее поле определяется суммой полей заряда q ₀ и индуцированных зарядов. Внутри сферы поле равно нулю.

Пример 2. При производстве капроновых нитей две из них приобрели электростатический заряд вследствие трения и плохого заземления. Расстояние между нитями а = 1 см, линейная плотность заряда τ₁ = τ₂ = 10^-6 Кл/м. Определить напряженность электростатического поля на расстоянии b = 1 см справа от ближайшей нити. Есть ли опасность пробоя воздуха в этой точке? Электростатический пробой в воздухе возникает при напряженности электрического поля Е₀ = 3·10⁶ В/м.

Решение: По принципу суперпозиции электростатических полей имеем:

.

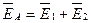Так как вектора 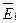и 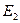направлены по одной прямой в одну сторону, то величину Е_А можно найти как сумму

.

Будем рассматривать нити как бесконечно длинные. Для бесконечно длинной заряженной нити с линейной плотностью заряда τ по теореме Остроградского-Гаусса имеем:

,

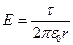где r = расстояние от нити.

Тогда

.

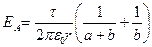Подставим исходные данные и произведем вычисления:

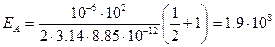В/м.

Таким образом, 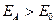, следовательно, на расстояниях r < b от нитей возможен пробой воздуха.

Пример 3. В трех вершинах квадрата со стороной a = 40 см находятся одинаковые положительные заряды по q ₁ = q ₂ = q ₃ = 5·10^-9 Кл каждый. Найти напряженность E поля в четвертой вершине.

Решение: По принципу суперпозиции электрических полей (рис. 20) для точки А находим:

, (1)

где 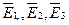– напряженности полей, созданных зарядами q ₁, q ₂, q ₃ соответственно в точке А. Запишем уравнение (1) в проекциях на выбранные направления:

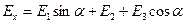
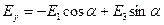(2)

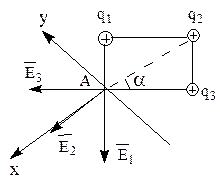
Рис. 20. Графическое изображение системы зарядов

Учитывая, что ; ,

, ,

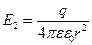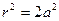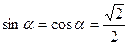и подставляя эти выражения в уравнения (2), найдем:

; .

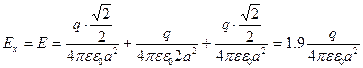Подставив числовые данные, получим

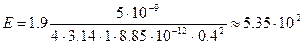В/м.

Пример 4. С поверхности бесконечного равномерно заряженного (τ = 50 нКл/м) цилиндра вылетает α -частица (υ ₀ = 0). Определите кинетическую энергию Е _к2 α -частицы в точке 2 на расстоянии 8 R от поверхности цилиндра (рис. 21).

Решение: Так как силы электростатического поля являются консервативными, то для определения кинетической энергии α -частицы в точке 2 воспользуемся законом сохранения энергии, записанном в виде Е 1 = Е 2, где Е 1 и Е 2 – полные энергии α -частицы в точках 1 и 2. Так как Е 1 = Е к1+ Е п1 и Е 2 = Е к2+ Е п2 (Ек – кинетическая энергия частицы; Е п – потенциальная энергия частицы), то, учитывая, что Е к1 = 0 (υ 0 = 0), можно записать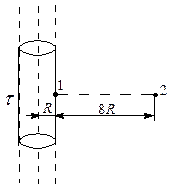

Рис. 21

Е п₁ = Е к₂+ Е п₂, откуда Е к₂ = Е п₁ – Е п₂ = q (φ ₁ – φ ₂), где q – заряд α -частицы; φ ₁ и φ ₂ – потенциалы точек 1 и 2.

Потенциал d φ, создаваемый этой заряженной частицей, можно определить по формуле .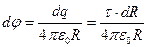

Согласно принципу суперпозиции электрических полей, потенциал электрического поля, создаваемого заряженным цилиндром (стержнем) в точке 2 найдем интегрированием этого выражения

.

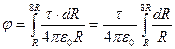Выполним интегрирование

.

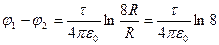Тогда

.

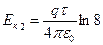Подставляя данные, получим

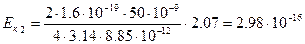Кл

или 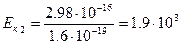эВ = 1.9 кэВ.

Пример 5. Как изменится емкость плоского воздушного конденсатора, если между его обкладками поместить диэлектрическую пластинку (ε = 6), толщина которой равна половине расстояния между обкладками?

Решение: После того как между обкладками конденсатора поместили диэлектрическую пластинку, его можно рассматривать как батарею последовательно соединенных конденсаторов: первый – заполненный диэлектриком с емкостью , второй – воздушный с емкостью 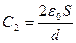, расстояния между обкладками в каждом d /2 (d – расстояние между обкладками конденсатора).

Общая емкость батареи определится правилом последовательного соединения конденсаторов: .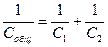

Емкости С ₁ и С ₂ можно выразить через первоначальную емкость плоского воздушного конденсатора ; ; .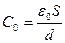

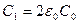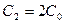Отсюда общая емкость батареи будет равна: .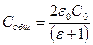

Подставляя значение ε = 6, получаем ответ

.

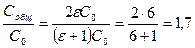Пример 6. Медный шар массой m = 1 кг содержит N = 1·10¹⁰ нескомпенсированных элементарных зарядов. Определить емкость шара и его потенциал. Плотность меди ρ = 8,9·10³ кг/м³.

Решение: Емкость шара определим по формуле .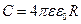

Радиус шара можно определить из формулы его объема .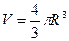

Теперь воспользуемся формулой плотности и подставим в нее значение для объема: 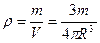, откуда .

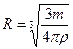Подставим это выражение в формулу для емкости, тем самым ответив на вопрос задачи:

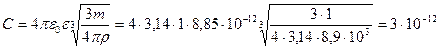Ф.

Потенциал определим из формулы емкости проводника:

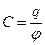, откуда В.

Пример 7. Электрон с некоторой начальной скоростью υ ₀ влетает в плоский конденсатор параллельно пластинам на равном расстоянии от них. К пластинам конденсатора приложена разность потенциалов U = 300 В. Расстояние между пластинами d = 2 см, длина конденсатора l = 10 см. Какова должна быть предельная начальная скорость υ ₀ электрона, чтобы электрон не вылетал из конденсатора?

Решение: Электрон в плоском конденсаторе будет двигаться по параболе (рис. 22), подобно горизонтально брошенному телу в поле силы тяжести. Траекторию электрона можно спроецировать на оси X и Y по двум взаимно перпендикулярным направлениям. Ось X – горизонтально, ось Y – вертикально вниз. На электрон в конденсаторе действует постоянная сила F = eE, направленная вдоль

Рис. 22. Движение электрона в плоском конденсаторе

оси Y, под действием которой он получит ускорени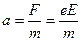е , где 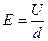– напряженность поля конденсатора. Следовательно, вдоль оси Y движение электрона равноускоренное с нулевой начальной скоростью, т. к. проекция υ ₀ на ось X равна нулю. Вдоль оси Х на электрон не действуют никакие силы, следовательно, вдоль оси Х движение происходит с постоянной скоростью υ ₀. Пролетая длину l конденсатора за время 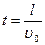, электрон отклонится на расстояние .

Чтобы электрон не вылетел из конденсатора, надо, чтобы ,

где d – расстояние между пластинами конденсатора.

Отсюда .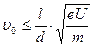

Подставляя данные, получим предельную начальную скорость для электрона

м/с.

Пример 8. Коаксиальный электрический кабель состоит из центральной жилы и концентрической по отношению к ней цилиндрической оболочки, между которыми находится изоляция ε = 3,2. Найти ёмкость С ₁ единицы длины такого кабеля, если радиус жилы R ₁ = 1,3 см, радиус оболочки R ₂ = 3,0 см (рис. 23).

Решение: Кабель можно рассматривать как цилиндрический конденсатор.

Ёмкость конденсатора: ,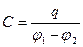

где q – заряд на жиле, (φ₁ - φ₂) – разность потенциалов между жилой и оболочкой.

Ёмкость единицы длины кабеля: 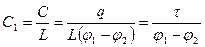, где τ - линейная плотность заряда. Разность потенциалов связана с напряженностью 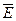электрического поля, направленного вдоль радиальных прямых от жилы к оболочке: .

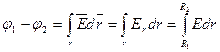Рис. 23. Схематическое изображение кабеля

Напряженность поля заряженной жилы (нити):

.

Тогда .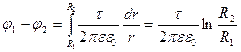

Следовательно, .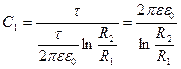

Подставив данные, получим

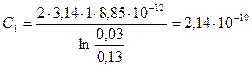Ф/м или 214 пФ/м.

Date: 2015-08-15; view: 4006; Нарушение авторских прав