
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Элементы механики жидкостей и газов. где ∆F – сила, действующая со стороны жидкости на единицу площади поверхности ∆S
|
|
· Давление в жидкости
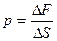 ,
,
где ∆ F – сила, действующая со стороны жидкости на единицу площади поверхности ∆ S. За единицу давления в СИ принят паскаль (Па).
· Закон Архимеда
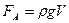 ,
,
где ρ – плотность жидкости, кг/м3; V – объем погруженной в жидкость части тела, м3.
· Гидростатическое давление
 ,
,
где h – высота столба жидкости.
· Закон Паскаля: давление в любом месте покоящейся жидкости одинаково по всем направлениям, причем давление одинаково передается по всему объему, занятому покоящейся жидкостью (рис. 8)
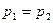 , или
, или  .
.

Рис. 8. Принцип действия гидравлического пресса
· Уравнение Бернулли
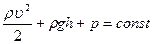 ,
,
где ρ – плотность жидкости; р – статическое давление; 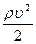 – динамическое давление.
– динамическое давление.
· Коэффициент динамической вязкости жидкости
 ,
,
где R – радиус капилляра длиной l; V – объем вытекаемой жидкости; t – время истечения жидкости.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. В два колена U -образной трубки налиты вода и масло, разделенные ртутью. Поверхности раздела ртути и жидкостей в обоих коленах находятся на одной высоте. Определить высоту столба воды, если высота столба масла 20 см. Плотность воды 1000 кг/м3, плотность масла 900 кг/м3.
Решение: Согласно закону Паскаля давление в обоих коленах трубки одинаково
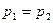 , (1)
, (1)
где 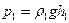 и
и  – давления в левом и правом коленах; ρ 1 и ρ 2 – плотности воды и масла.
– давления в левом и правом коленах; ρ 1 и ρ 2 – плотности воды и масла.
Подставляя выражения для ρ 1 и ρ 2 в равенство (1), получим
 ,
,
откуда  м.
м.
Пример 2. Однородное тело плавает на поверхности керосина так, что объем погруженной части составляет 0,92 всего объема тела. Определите объем погруженной части при плавании тела на поверхности воды.
Решение: Обозначим через V объем всего тела, V п – объем погруженной части тела, плавающего в керосине, V 'п – объем погруженной части тела, плавающего в воде.
На тело, плавающее в керосине, действуют сила тяжести  , выталкивающая сила керосина
, выталкивающая сила керосина 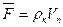 . Из условия плавания следует, что
. Из условия плавания следует, что 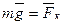 или
или
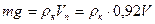 . (1)
. (1)
Аналогично запишем условие плавания тела в воде
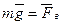 или
или  . (2)
. (2)
Из уравнений (1) и (2) получим
 ,
,
откуда  .
.
Пример 3. Цилиндрический сосуд с диаметром основания, равным высоте цилиндра, наполнен доверху водой. Найти разность Δ F сил давления воды на дно и стенку цилиндра. Плотность воды 1000 кг/м3, высота цилиндра Н = 20 см.
Решение: Разность сил найдем, отняв от силы давления F 2 воды на стенку силу давления F 1 на дно цилиндра: 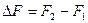 , где
, где  и
и 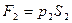 . Здесь р 1 – давление воды на дно цилиндра,
. Здесь р 1 – давление воды на дно цилиндра, 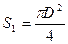 – площадь дна, р 2 – давление воды на стенку и
– площадь дна, р 2 – давление воды на стенку и 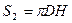 – площадь стенки цилиндра. Поскольку
– площадь стенки цилиндра. Поскольку  и согласно условию D = H,
и согласно условию D = H,
то 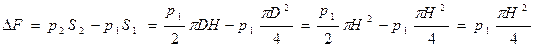 .
.
Давление воды на дно р 1 определим через плотность и высоту: 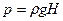 .
.
Тогда  Н.
Н.
Пример 4. Давление производимое на малый поршень гидравлического пресса, осуществляется посредством рычага (рис. 9), соотношение плеч которого  . Какой массы груз может быть поднят большим поршнем, если к длинному плечу рычага приложена сила F = 0,01 кН? Площади поршней S 1 = 10 cм2, S 2 = 500 см2, КПД пресса η = 0,75.
. Какой массы груз может быть поднят большим поршнем, если к длинному плечу рычага приложена сила F = 0,01 кН? Площади поршней S 1 = 10 cм2, S 2 = 500 см2, КПД пресса η = 0,75.
Решение: Определим вначале, какую силу F 2 развил бы большой поршень, если бы в узлах механизма отсутствовало трение и иные помехи, т.е. если бы КПД был равен 100 %. Согласно формуле гидравлического пресса:
 , откуда
, откуда  . (1)
. (1)
Здесь F 1 – сила, прилагаемая коротким плечом рычага к малому поршню. Эту силу определим, воспользовавшись правило м рычага: рычаг дает выигрыш в силе во столько раз, во сколько его длинное плечо длиннее короткого:
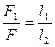 , откуда
, откуда 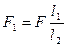 . (2)
. (2)
Подставим (2) в (1): 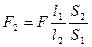 .
.
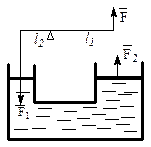
Рис. 9. Схема гидравлического пресса
Такое усилие развил бы пресс, если бы его КПД был равен 100 %. Но из-за различных помех оно станет меньше и будет:
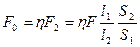 .
.
При равномерном подъеме груза сила тяжести  , приложенная к нему, будет уравновешена силой F 0, поэтому
, приложенная к нему, будет уравновешена силой F 0, поэтому 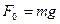 или
или 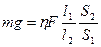 ,
,
откуда 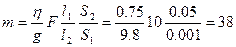 кг.
кг.
Date: 2015-08-15; view: 919; Нарушение авторских прав