Кинематика

· Положение материальной точки А (рис.1) в пространстве задается радиусом-вектором 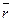(вектор, проведенный из начала координат в данную точку):

,

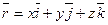где 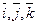– единичные векторы направлений; x, y, z – координаты точки.

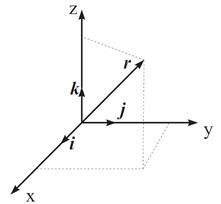
Рис. 1. Декартова система координат

Кинематические уравнения движения в координатной форме:

x = f ₁(t), y = f ₂(t), z = f ₃(t),

где t – время.

· Средняя скорость:

,

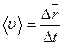где 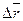– перемещение материальной точки за интервал времени Δ t.

В Международной системе (СИ) единицей расстояния является метр, единицей времени – секунда; поэтому скорость выражается в метрах в секунду (м/с).

Средняя путевая скорость:

,

где Δ s – путь, пройденный точкой за интервал времени Δ t. Путь Δ s в отличие от разности координат Δ х = х ₂ – х ₁ не может убывать и принимать отрицательные значения, т.е. Δ s ≥ 0.

Мгновенная скорость:

,

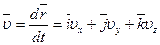где 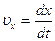; ; 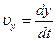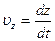– проекции скорости υ на оси координат.

Модуль скорости:

.

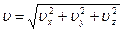· Ускорение

,

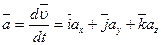где 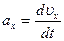; ; 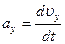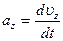– проекции ускорения а на оси координат; единица измерения ускорения метр на секунду в квадрате (м/с²).

Модуль ускорения:

.

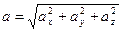При криволинейном движении (рис. 2) ускорение можно представить как сумму нормальной а _n и тангенциальной а_τ составляющих:

.

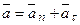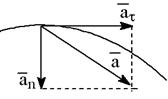
Рис. 2. Криволинейное движение точки (тела)

Модули этих ускорений:

; ; .

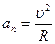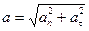где R – радиус кривизны в данной точке траектории.

· Кинематические уравнения прямолинейного равномерного движения (υ = const):

1) в векторной форме

,

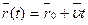где 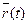– радиус-вектор, определяющий положение материальной точки в момент времени t; 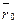– радиус-вектор, определяющий положение точки в начальный момент времени (t = 0);

2) в координатной форме (в проекции на координатные оси Оx, Oy, Oz)

x (t) = x ₀ + υ_xt; y (t) = y ₀ + υ_yt; z (t) = z ₀ + υ_zt,

x ₀, y ₀, z ₀ – начальные координаты; υ _x, υ _y, υ _z – проекции скорости на координатные оси.

· Кинематические уравнения прямолинейного равноускоренного движения (a = const):

1) в векторной форме

,

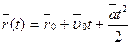где 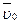– начальная скорость (скорость материальной точки в момент времени t = 0);

2) в координатной форме

; ; ,

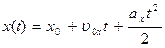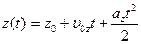где υ _0x, υ _0y, υ _0z – проекции начальной скорости на координатные оси; a _x, a _y, a _z – проекции ускорения.

· Скорость точки при равноускоренном движении:

1) в векторной форме

;

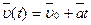2) в координатной форме

; ; .

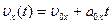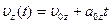· Средняя угловая скорость:

,

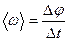где Δ φ – угловое перемещение за время Δ t; единица измерения угловой скорости радиан на секунду (рад/с).

· Мгновенная угловая скорость:

,

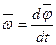в проекции на ось вращения

.

· Угловое ускорение

,

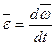в проекции на ось вращения

,

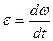единица измерения углового ускорения радиан на секунду в квадрате (рад/с²).

· Кинематическое уравнение равномерного (ω = const) вращения в проекции на ось вращения:

,

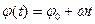где φ ₀ – начальное угловое ускорение.

· Частота вращения

или ,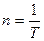

где N – число оборотов, совершаемое телом за время t; T – период вращения (время одного полного оборота); единица измерения частоты секунда в минус первой степени (с^-1).

Угловое перемещение φ и угловое ускорение ω связаны с числом оборотов, частотой вращения и периодом вращения соотношением:

; ; .

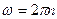· Кинематическое уравнение равноускоренного вращения в проекции на ось вращения:

,

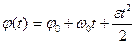где ω ₀ – начальная угловая скорость.

Угловая скорость при равноускоренном вращении

.

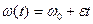Число оборотов N связано со средней частотой 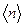вращения соотношением:

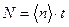
При равноускоренном вращении 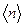есть полусумма начальной n ₀ и конечной n мгновенными частотами вращения:

.

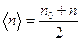· Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами:

,

где φ – угол поворота тела; s – путь, пройденный точкой по дуге окружности радиуса R.

Скорость точки (линейная)

; ;

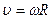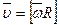ускорение точки

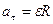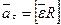; (тангенциальное);

(нормальное).

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

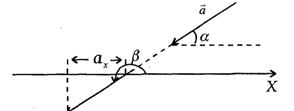
Пример 1. Определить проекцию вектора на ось ОХ, полагая, что угол α задан (рис. 3 а,б).

Решение: Опустим перпендикуляры с концов вектора на ось ОХ. Проекция вектора на ось ОХ равна

.

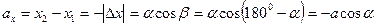Угол β отсчитывается от положительного направления оси ОХ до вектора против часовой стрелки, причем вектор нужно перенести параллельно самому себе так, чтобы его начало лежало на оси ОХ (рис. 3б).

Рис. 3а Рис. 3б

Пример 2. Вертолет начал снижаться с ускорением 0,2 м/с². Лопасть винта вертолета имеет длину 5 м и совершает 300 об/мин. Определите число оборотов лопасти за время снижения вертолета на 40 м, линейную скорость и центростремительное ускорение.

Решение: Искомое число оборотов лопасти винта совершают за время, равное времени снижения вертолета. Уравнение движения вертолета: 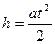следовательно, время снижения: 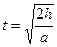, а число оборотов: оборотов.

Линейная скорость концов лопасти винта: м/с.

Центростремительное ускорение конца лопасти:

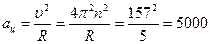м/с².

Пример 3. Вал начинает вращаться и в первые t = 10 с совершает N = 50 оборотов. Считая вращение вала равноускоренным, определить угловое ускорение и конечную угловую скорость.

Решение: Поскольку начальная угловая скорость равна нулю, уравнение движения и формула угловой скорости:

, .

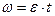Так как угловое перемещение за один полный оборот равно 2π, то полное угловое перемещение вала, соответствующее N оборотам, φ = 2πN. Подставив это выражение в уравнение движения, получим ,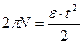

откуда

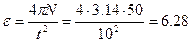рад/с².

Date: 2015-08-15; view: 709; Нарушение авторских прав