Динамика вращательного движения твердого тела вокруг неподвижной оси

· Момент силы 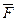, действующей на тело, относительно оси вращения

,

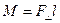где – проекция силы 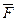на плоскость, перпендикулярную оси вращения; l – плечо силы 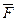(кратчайшее расстояние от оси вращения до линии действия силы). Единица измерения момента сил ньютон на метр (Н∙м).

· Момент инерции относительно оси Oz:

а) материальной точки

,

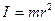где m – масса материальной точки; r – расстояние от нее до оси вращения;

б) системы материальных точек

,

где m_i – масса i – й материальной точки; r_i – расстояние от этой точки до оси Oz. Единица измерения момента инерции килограмм на метр в квадрате (кг∙м²).

· Теорема Штейнера: момент инерции тела, относительно произвольной оси равен моменту его инерции I_C относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:

.

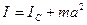· Момент силы, действующей на тело, относительно точки О

,

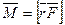где 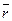– радиус-вектор, направленный от точки О, относительно которой определяется момент силы, к точке приложения силы .

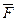· Момент силы, действующей на тело, относительно оси Oz (проекция вектора 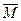на ось Oz)

,

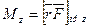или

,

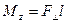где – проекция силы 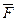на плоскость, перпендикулярную оси Oz; l – плечо силы 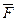(кратчайшее расстояние от оси до линии действия силы).

· Момент импульса материальной точки относительно точки О

,

где 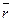– радиус-вектор, направленный от точки О, относительно которой определяется момент импульса, к движущейся материальной точке, импульс которой равен . Единица измерения момента импульса килограмм на метр в квадрате на секунду (кг∙м²/с)

· Момент импульса материальной точки относительно оси Oz (проекция вектора 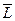на ось Oz)

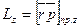
или

,

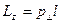где – проекция импульса на плоскость, перпендикулярную оси Oz; l – плечо импульса (кратчайшее расстояние от оси Oz до линии, вдоль которой движется материальная точка).

· Момент импульса твердого тела, вращающегося относительно оси Oz

.

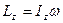· Основной закон динамики вращательного движения:

а) относительно неподвижной точки

,

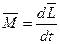где 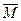– главный момент всех внешних сил, действующих на систему, относительно неподвижной точки О; – скорость изменения момента импульса системы относительно той же точки;

б) относительно неподвижной оси Oz

,

где M_z и L_z – главный момент внешних сил и момент импульса системы относительно оси Oz, или для твердого тела с неизменным моментом инерции

,

где I_z – момент инерции твердого тела, ε – угловое ускорение.

· Работа постоянного момента силы M_z, действующего на вращающееся вокруг оси Oz тело

,

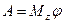где φ – угол поворота тела.

· Мгновенная мощность

.

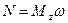· Кинетическая энергия тела, вращающегося относительно неподвижной оси Oz

.

· Кинетическая энергия тела, катящегося по плоскости

,

где υ_С – скорость центра масс тела, I_z – момент инерции тела относительно оси Oz, проходящей через его центр масс.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Через блок, укрепленный на горизонтальнойоси (рис.6), проходящей через его центр, перекинута нить, к концам которой прикреплены грузы m ₁ = 0,3 кг и m ₂ = 0,2 кг. Масса блока m = 0,3 кг. Блок считать однородным диском. Найти ускорение грузов.

Решение: Система состоит из трех тел: грузов m ₁и m ₂, движущихся поступательно, и блока m, вращающегося относительно неподвижной оси, проходящей через центр инерции блока. Груз m ₁ находится под действием двух сил: силы тяжести 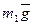и силы натяжения нити 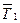. Груз m ₂ также находится под действием двух сил: силы тяжести и силы натяжения нити . Запишем 2-й закон Ньютона для грузов:

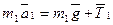, (1)

. (2)

Блок вращается вокруг неподвижной горизонтальной оси, проходящей через его центр, следовательно, момент силы тяжести блока и момент силы реакции оси равны нулю. Если предположить, что нить не скользит относительно блока, то вращают блок только силы натяжения нити.

Запишем основное уравнение динамики вращательного движения для блока:

, (3)

где 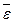– угловое ускорение, I – момент инерции блока, 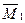и 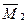– моменты сил и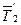

Рис. 6. Схема движения грузов

Если нить невесома, то силы натяжения вдоль нити с каждой стороны блока одинаковы по модулю, то есть: , 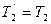. Ускорения обоих грузов считаем равными по модулю на основании нерастяжимости нити. Если нить не проскальзывает относительно блока, то касательное ускорение его точек, соприкасающихся с нитью, равно ускорению нити в любой ее точке и ускорению грузов: .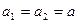

Для перехода к скалярным соотношениям для описания движения грузов введем ось Y. Теперь векторные уравнения (1 и 2) можно заменить скалярными:

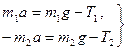(4)

Моменты сил и направлены по оси вращения, но в противоположные стороны. Примем направление вектора 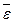за положительное. Тогда момент силы относительно оси вращения будет положительным, а момент силы – отрицательным. Векторное уравнение (3) можно переписать в виде:

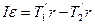, или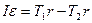

где: r – радиус блока.

Учитывая, что момент инерции однородного диска 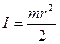и связь линейного и углового ускорений 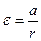, получаем:

(5)

Из уравнений (4) выразим силы натяжения нитей:

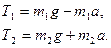
Подставим в (5), получим:

.

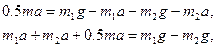
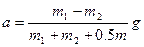м/с².

Пример 2. Мальчик катит обруч по горизонтальной дороге со скоростью 2 м/с. На какое расстояние может вкатиться обруч на горку за счет его кинетической энергии? Уклон горки 10 м на каждые 100 м пути.

Решение: У подножия горки обруч обладает запасом кинетической энергии:

где: 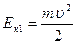– кинетическая энергия поступательного движения обруча; – кинетическая энергия вращательного движения.

Вкатившись на горку на максимально возможное расстояние (высота горки в этом месте h рис. 7), обруч приобретет запас потенциальной энергии 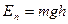, кинетическая энергия в этом положении равна нулю.

Пренебрегая трением, воспользуемся законом сохранения энергии: ,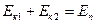

Учтем, что момент инерции обруча относительно оси, проходящей через центр инерции: I = mr ², где: m – масса обруча, r – радиус обруча. Угловая скорость обруча ω связана с линейной скоростью υ ’ точек, лежащих на поверхности обруча: .

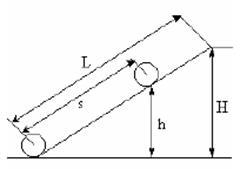Рис. 7. Движение обруча

Поскольку за один полный оборот точка, лежащая на поверхности обруча, проходит путь 2πr и центр масс смещается тоже на расстояние 2πr, то υ’ = υ. Таким образом

.

Тогда

,

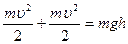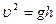, откуда .

Так как ,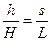

то м.

Пример 3. В общей точке подвеса подвешены шарик на нити длины l и однородный стержень длины L, отклоненный в сторону на некоторый угол. При возвращении стержня в положение равновесия происходит упругий удар. При каком соотношении между массами стержня M и шарика m точки удара стержня и шара будут двигаться после удара с равными скоростями в противоположных направлениях?

Решение:В самый начальный момент удара стержень вращается с некоторой скоростью ω ₀. Систему «стержень-подвес-нить с шаром» можно считать замкнутой, поэтому после удара выполняется закон сохранения момента импульса.

Т.е. момент импульса относительно точки подвеса остается прежним:

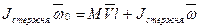
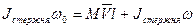
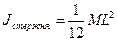, т.к. стержень вращается вокруг закрепленного конца;

.

,

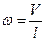. (1)

При упругом ударе выполняется закон сохранения энергии, т.е. кинетическая энергия остается постоянной:

.

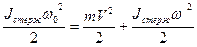Тогда

,

,

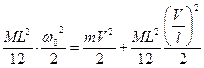
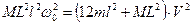. (2)

Сопоставим (1) и (2)

,

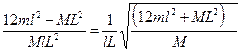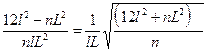
Решим данное уравнение относительно n.

,

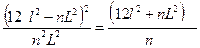
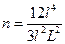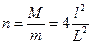
Ответ: .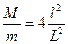

Date: 2015-08-15; view: 2144; Нарушение авторских прав