Дәрістің жоспары

1. Қатты дененің ілгерілемелі қозғалысының дифференциалдық теңдеуі

2. Қатты дененің айналмалы қозғалысының дифференциалдық теңдеуі

3. Қатты дененің жазық қозғалысының дифференциалдық теңдеуі

Абсолют қатты денені механикалық жүйенің дербес жағдайы деп қарастыруға болатыны белгілі. Қатты дене динамикасының есептерін шешу үшін бұл денеге әсер ететін күштерді және кеңістікте дененің орнын анықтайтын параметрлерді байланыстыратын теңдеулерді табу керек. Бұл тәуелділіктерді жүйе динамикасының жалпы теоремалардан алуға болады.

Дене қозғалысының дифференциалдық теңдеулері бойынша есептердің екі түрін шешуге болады: 1) дененің берілген қозғалысы бойынша оған әсер ететін сыртқы күштерді анықтау; 2) денеге әсер ететін берілген қүштері мен қозғалысының бастапқы шарттары бойынша дене қозғалысының кинематикалық теңдеулерін анықтау.

Ілгерілемелі қозғалыстағы бұрыштық жылдамдығы мен оның массалар центріне қатысты алынған қозғалыс мөлшерінің бас моменті нөлге тең. Механикалық жүйенің массалар центрінің қозғалуы туралы теоремасы қарастырып отырған жағдай үшін былай жазылады:

,

мұнда 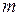- дененің массасы; 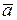- дене массалар центрінің үдеуі, ол ілгерілемелі қозғалыстағы дененің кез келген нүктесінің үдеуіне тең.

Бұл теңдеуді қатты дене ілгерілемелі қозғалысының дифференциалдық теңдеудің векторлық түрінде жазуға болады:

.

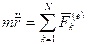Жалпы жағдайда ілгерілемелі қозғалыстағы дененің еркіндік дәреже саны үшке тең және оның қозғалысын декарттық координат жүйесінде массалар центрінің қозғалысы арқылы беруге болады. Декарттық өстерге проекциялары:

.

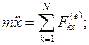
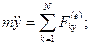
Бұл жағдайда бастапқы шарттары мына түрде жазылады: уақыт 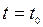болғанда .

Табиғи өстеріне проекцияласақ (массалар центрінің қозғалысы табиғи әдіспен берілгенде бұл жағдайда дененің еркіндік дәреже саны бірге тең), алатынымыз:

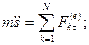
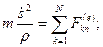
, мұнда 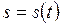- траектория бойымен массалар центрінің қозғалысының заңы. Бастапқы шарттар бұл жағдайда мына түрге келеді: 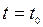болғанда .

Айналмалы қозғалыстағы қатты дененің еркіндік дәреже саны бірге тең. Қатты дене айналмалы қозғалысының дифференциалдық теңдеуін қорытып алу үшін механикалық жүйенің қозғалыс мөлшерілерінің бас моментінің өзгеруі туралы теоремасын қолданайық:

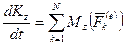, мұнда 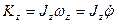. Онда 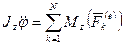. Бұл формула қозғалмайтын өске қатысты қатты дене айналмалы қозғалысының дифференциалдық теңдеуі деп аталады. Оны былай да жазуға болады:

немесе .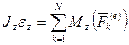

Қозғалмайтын өске қатысты қатты дене айналмалы қозғалысының бастапқы шарттары: уақыт 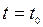болғанда .

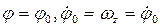Дененің жазық-параллель қозғалысының дифференциалдық теңдеулерін массалар центрінің қозғалуы туралы теоремасынан және массалар центріне қатысты салыстырмалы қозғалыста қозғалыс мөлшерілерінің бас моментінің өзгеруі туралы теоремасынан қорытып алайық.

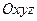қозғалмайтын координаттық жүйені таңдап алайық. Онда дененің массалар центрі үшін алатынымыз: 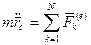және қозғалмалы координаттық жүйесін еңгізейік, оның басы дененің массалар центрде және 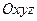жүйеге қатысты ол ілгерілемелі қозғалады. Айтып кеткен координаттық жүйелерінің жазықтықтары және 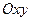дененің массалар центрі қозғалатын жазықтықпен дәл келеді деп ұйғарайық. Салыстырмалы қозғалыста массалар центріне қатысты қозғалыс мөлшерілерінің бас моментінің өзгеруі туралы теорема қатты дене үшін қозғалмалы координаттық жүйенің өсіне проекция түрінде былай өрнектеледі:

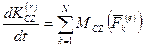, мұнда 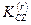- қозғалмалы өске қатысты алынған дененің қозғалыс мөлшерілерінің бас моменті

.

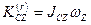Мұнда 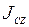- қозғалыс жазықтығына перпендикуляр болып келетін өске қатысты дененің инерция моменті.

Онда өске қатысты дене айналуының дифференциалдық теңдеуі былай болады: 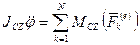. Жалпы жағдайда бастапқы шарттарды былай беруге болады; уақыт 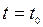болғанда 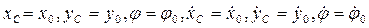, немесе 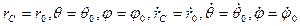, немесе .

Дененің еркіндік дәреже санына қарап оның қозғалысын бейнелеу саны бірден үшке дейін жалпыланған координаттарды қолдануға болады.

Өзіндік бақылау сұрақтары:

1. Қозғалмайтын өске қатысты дененің айналуы бірқалыпты болатын жағдайы қандай?

2. Өске қатысты қатты дененің инерция моменті нені сипаттайды?

3. Дене формасы мен өлшемдері дененің ілгерілемелі және айналмалы қозғалыстарына қандай ықпалы болады? Бұл жағдай қозғалыс теңдеулерінде қалай және қайда көрсетіледі?

Date: 2015-08-15; view: 697; Нарушение авторских прав