Жүйенің қозғалыс мөлшерінің өзгеруі туралы теорема

n материялық нүктеден тұратын механикалық жүйені қарастырайық. Нүктелердің үдеуі жылдамдық векторларының бірінші туындысы екенін ескеріп (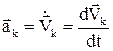), жүйе қозғалысының (4.3.1) дифференциалдық теңдеулерін қайтадан жазайық:

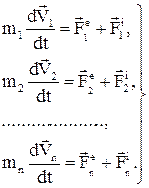
енді барлық теңдеулерді қосайық:

.

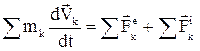Соңғы теңдеудің сол жағын түрлендіріп, жүйенің ішкі күштерінің қасиетін ескерсек () мынаны аламыз:

.

Бұл теңдеудегі 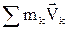-ны (4.3.5)-ке сәйкес 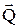арқылы алмастырсақ жүйенің қозғалыс мөлшерінің өзгеруі туралы теореманың дифференциалдық түрін аламыз:

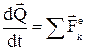. (4.3.7)

Теорема: механикалық жүйенің қозғалыс мөлшері векторының уақыт бойынша туындысы жүйеге әсер ететін барлық сыртқы күштердің геометриялық қосындысына тең.

(4.3.7) теңдеуі декарттық координата жүйесінің өстеріне проекцияланған үш скаляр теңдеуге пара-пар:

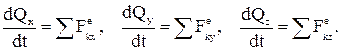(4.3.8)

Осы теореманы басқа түрде жазуға болады. Ол үшін механикалық жүйенің бастапқы 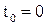уақыттағы қозғалыс мөлшерін 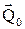деп, ал уақыттағы қозғалыс мөлшерін 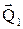деп белгілейік. (4.3.7) теңдеуінің екі жағын да 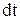-ға көбейтіп, интегралдайық:

.

Нәтижесінде мынаны аламыз:

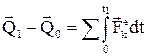
немесе, оң жақтағы интегралдар сыртқы күштердің импульстері болғандықтан:

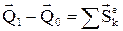, (4.3.9)

(4.3.9) теңдеуі жүйенің қозғалыс мөлшерінің өзгеруі туралы теореманың интегралдық түрін береді: кез келген уақыт аралығындағы жүйенің қозғалыс мөлшерінің өзгеруі осы уақытта жүйеге әсер ететін барлық сыртқы күштердің импульстерінің геометриялық қосындысына тең.

Есеп шығарғанда (4.3.9) векторлық теңдеуді декарттық координата жүйесінің өстеріне проекциялау керек:

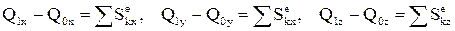. (4.3.10)

Жүйенің қозғалыс мөлшерінің өзгеруі туралы теоремадан қозғалыс мөлшерінің сақталу заңдарын аламыз:

1. Егер жүйеге әсер ететін барлық сыртқы күштердің геометриялық қосындысы нөлге тең болса, онда жүйенің қозғалыс мөлшерінің векторының шамасы да, бағыты да өзгермейді.

2. Егер жүйеге әсер ететін барлық сыртқы күштердің бір өске проекциясының қосындысы нөлге тең болса, онда жүйенің қозғалыс мөлшерінің осы өске проекциясы тұрақты болады.