Марковские процессы

1.5.1. Понятие о стохастических процессах

Стохастический процесс представляет собой множество случайных величин, образующих упорядоченную последовательность.

Последовательность случайных величин в процессе можно представить в виде X (t), где t – параметр процесса (обычно время).

Значения, принимаемые случайными величинами в процессе, образуют пространство состояний.

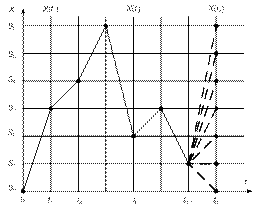
На рис. 1.15 показана конкретная реализация процесса на отрезке времени (t ₀, t _n–1). По оси абсцисс отложен дискретный параметр процесса t, а по оси ординат – дискретная случайная величина X, которая является множеством и включает в себя семь состояний объекта наблюдения (S ₀– S ₆). В данном случае множество X является пространством состояний (X { S ₀, S ₁, S ₂, S ₃, S ₄, S ₅, S ₆}). Для параметра процесса t _i X (t _i) = S ₂.

В большинстве прикладных задач целью является вычисление безусловного распределения случайной величины X (t _n), которое зависит только от реализации процесса в интервале от t _n–1 до t _n.

Рис. 1.15. Конкретная реализация процесса в интервале (t 0, t n–1)

1.5.2. Марковские процессы

Существует важный класс стохастических процессов, в которых вероятность случайной величины в момент времени t _n зависит от значения случайной величины в момент времени t _n–1 и не зависит от конкретного вида реализации процесса до времени t _n–1. Такой процесс называют процессом без последствия. Процессы, обладающие этим свойством, называют Марковскими процессами.

В Марковском процессе параметр t и пространство состояний X (t) могут быть как дискретными, так и непрерывными. Мы рассмотрим только процессы с непрерывными параметрами, при этом будем иметь в виду только дискретные и конечные пространства состояний.

Рассмотрим Марковский процесс X (t) с непрерывным временным параметром t. Введём обозначения: t _n–1 = t, t _n = t + D t.

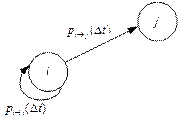
В процессе рассмотрим два состояния: i -е, в котором находится объект в момент времени t _n–1; j -е, в которое объект может перейти, а может и не перейти в момент времени t _n (рис. 1.16). Тогда вероятность перехода из i -го состояния в j -е запишется следующим образом:

.

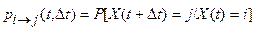(1.57)

Рис. 1.16. Переход из состояния i в состояние j или в само себя

Будем рассматривать только однородные Марковские процессы, в которых p_i®j зависят только от D t.

Тогда при D t →0 вероятности переходов принимают вид

,

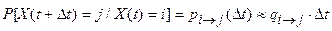(1.58)

.

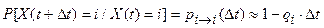(1.59)

Здесь p_i→i (D t) – вероятность того, что за промежуток времени D t не произойдёт смены состояния процесса при условии, что процесс находится в состоянии i в начале этого промежутка.

q_i→j, q_j→i – интенсивности переходов из состояния i в состояние j и наоборот;

q_i – интенсивность перехода из состояния i в любое другое состояние, кроме состояния i:

,

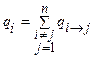(1.60)

где n – число всех возможных состояний.

Так как события «переход из i -го в j -е состояние» (i®j) и «переход из i -го в i -е состояние» (i®i) являются полной группой событий, то

.

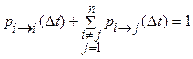(1.61)

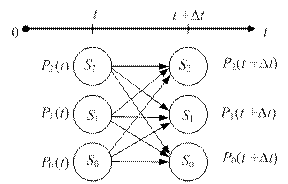
Во многих приложениях требуется определить безусловные вероятности состояний для момента времени (t + D t), зная вероятности состояний в момент времени t (рис. 1.17).

Для этого используется метод пространства состояний, в котором используется система дифференциальных уравнений Чемпена – Колмогорова (см. п 5.1).

Рис.1.17. Возможные переходы для процесса, в котором объект может находиться в трех состояниях

Вопросы для самоподготовки

1. В чем различие между понятиями «априорная вероятность» и «апостериорная вероятность»?

2. Дать определение классической, геометрической и статистической вероятностей.

3. Что называется условной вероятностью?

4. Что называется случайной величиной? Приведите примеры дискретной и непрерывной случайных величин.

5. В чем разница между законами распределений дискретной и непрерывной случайными величинами?

6. Дайте определение интенсивности потока событий?

8. Какие числовые характеристики случайных величин Вы знаете? Приведите их формулы для непрерывной и дискретной случайных величин.

9. Дайте определение интегральной функции распределения вероятности непрерывной случайной величины.

10. Дайте определение плотности распределения вероятности непрерывной случайной величины.

11. Какие законы распределения непрерывной случайной величины Вы знаете? Приведите их аналитические формулы.

12. Какому закону распределения соответствует постоянная интенсивность потока случайной величины?

13. Чем отличается Марковский процесс от стохастического?

14. Какой процесс называется однородным Марковским процессом?

15. Что такое параметр Марковского процесса и пространство состояний?

Глава 2. Основные понятия теории надежности

Date: 2015-07-25; view: 370; Нарушение авторских прав