
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Статистическая обработка результатов работы невосстанавливаемых объектов. Выбор закона распределения вероятности наработки до отказа
|
|
4.2.1. Постановка задачи
По результатам испытаний N невосстанавливаемых одинаковых объектов получена статистическая выборка – массив наработки до отказа каждого из N объектов: Ta = {a 1 ,a 2 ,…,aN}. Выборка характеризует случайную величину – наработку до отказа. Необходимо выбрать закон распределения случайной величины.
4.2.2.Алгоритм обработки результатов экспериментов
А. Формирование статистического ряда.
При большом числе испытываемых объектов получаемый массив наработки Ta = {a 1 ,a 2 ,…,aN} является громоздкой формой записи случайной величины. Для компактности и наглядности выборку следует представить в графическом изображении статистического ряда, которое называется гистограмма наработки до отказа. Для этого необходимо выполнить следующее:
1. Установить интервал наработки [ t min, t max] и его длину xt = t max –– t min, где t min и t max – минимальная и максимальная величины наработки до отказа.
2. Разбить интервал наработки на «k» интервалов (k = 6¸10) равной длины с шагом ∆t:
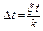 или или 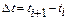 . .
| (4.1) |
3. Подсчитать частоту появления отказов:
 , ,
| (4.2) |
где D n (ti, ti+1) – число объектов, отказавших в интервале времени [ ti, ti+1 ]. Очевидно, что
 . .
| (4.3) |
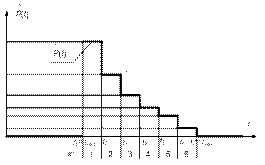
4. Полученный статистический ряд представить в виде гистограммы, которая строится следующим образом. По оси абсцисс t откладываются интервалы D t, на каждом из которых, как на основании, строится прямоугольник, высота которого пропорциональна (в выбранном масштабе) соответствующей частоте 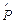 . Возможный вид гистограммы приведен на рис. 4.1.
. Возможный вид гистограммы приведен на рис. 4.1.
|
| Рис. 4.1. Гистограмма статистического ряда |
Б. Расчет эмпирических функций.
Расчет эмпирических функций включает в себя следующее:
– оценку вероятности отказа:
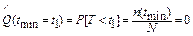 ; ;
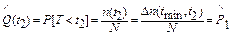 ; ;
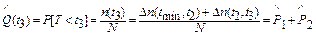 ;
………………………………………….. ;
…………………………………………..
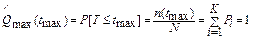 ; ;
| (4.4) |
– оценку вероятности безотказной работы:
 ;
………………………. ;
……………………….
 ; ;
| (4.5) |
– оценку плотности распределения отказа:
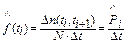
| (4.6) |
(ее график совпадает по форме с гистограммой, представленной на рис. 4.1, и отличается лишь по масштабу);
– оценку интенсивности отказов:
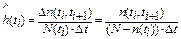 . .
| (4.7) |
Примеры форм кривых зависимости вероятности безотказной работы 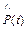 , вероятности отказа,
, вероятности отказа,  и интенсивности отказа
и интенсивности отказа  приведены на рис. 4.2.
приведены на рис. 4.2.
В. Расчет статистических оценок числовых характеристик.
Расчет статистических оценок числовых характеристик включает в себя следующее:
– оценку средней наработки до отказа, которая может быть вычислена двумя способами:
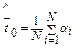 (см. табл. 3.1); (см. табл. 3.1);
| (4.8) |
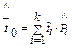 , ,
| (4.9) |
где 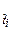 – середина i -го интервала наработки,
– середина i -го интервала наработки,
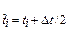 ; ;
| (4.10) |
|
| а) |

|
| б) |
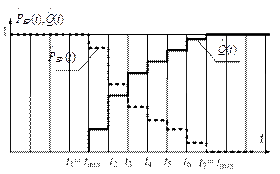
Рис. 4.2. Графики статистических оценок вероятности безотказной работы 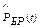 , вероятности отказа , вероятности отказа 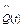 и интенсивности отказа и интенсивности отказа 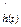 : а – графики статистических оценок : а – графики статистических оценок 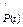 и и 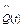 ; б – графики статистической оценки ; б – графики статистической оценки 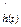
|
– оценку дисперсии наработки до отказа, которая может быть вычислена двумя способами:
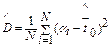 ; ;
| (4.11) |
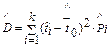 ; ;
| (4.12) |
– оценку среднего квадратического отклонения:
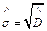 . .
| (4.13) |
Г. Выбор закона распределения случайной величины.
Он состоит в подборе аналитической функции, которая лучшим образом с точки зрения исследователя аппроксимирует эмпирические функции надежности. Выбор, в значительной мере процедура неопределенная и во многом субъективная, зависит от формы графиков зависимостей от времени показателей безотказности: вероятности безотказной работы 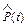 , вероятности отказа
, вероятности отказа  , плотности распределения отказов
, плотности распределения отказов 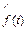 и интенсивности отказов
и интенсивности отказов  .
.
Пусть по тем или иным соображениям выбран гипотетический закон распределения, который задан плотностью распределения отказов в следующей форме:
 , ,
| (4.14) |
где а, b, с – неизвестные параметры распределения. Ими могут быть средняя наработка до отказа 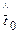 , дисперсия наработки до отказа
, дисперсия наработки до отказа  , ее среднее квадратическое отклонение
, ее среднее квадратическое отклонение 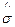 и другие величины.
и другие величины.
Требуется подобрать параметры так, чтобы f(t) наилучшим образом сглаживала график 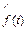 . При этом используется следующий прием: параметры а, b, с, … выбираются с таким расчетом, чтобы несколько важнейших числовых характеристик теоретического распределения были равны соответствующим статистическим оценкам. Например, для нормального распределения параметры а и b, математическое ожидание и среднее квадратическое отклонение теоретического распределения принимаются равными оценкам
. При этом используется следующий прием: параметры а, b, с, … выбираются с таким расчетом, чтобы несколько важнейших числовых характеристик теоретического распределения были равны соответствующим статистическим оценкам. Например, для нормального распределения параметры а и b, математическое ожидание и среднее квадратическое отклонение теоретического распределения принимаются равными оценкам 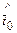 и
и 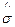 , т. е.
, т. е. 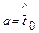 ,
,  .
.
На графике вместе с 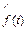 строится теоретическая зависимость плотности распределения отказов от времени
строится теоретическая зависимость плотности распределения отказов от времени  , что позволяет визуально оценить результаты аппроксимации (расхождение между
, что позволяет визуально оценить результаты аппроксимации (расхождение между 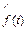 и
и  ). Более точная оценка результатов аппроксимации производится с помощью критерия согласия, который в данной работе не рассматривается.
). Более точная оценка результатов аппроксимации производится с помощью критерия согласия, который в данной работе не рассматривается.
Пример. При наблюдении за работой 30 однотипных невосстанавливаемых объектов был получен следующий статистический ряд наработок до отказа:
Ta = {20; 21; 23; 23; 27; 29; 30; 34; 36; 39; 42; 47; 49; 49; 52; 57; 58; 61; 67; 72; 75; 84; 90; 97; 108; 117; 129; 153; 175; 220} (ч).
Разбив интервал наработки на k = 10 участков, определить:
1) зависимость от времени показателей безотказности: вероятности безотказной работы 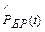 , вероятности отказа
, вероятности отказа  , плотности распределения отказов
, плотности распределения отказов 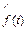 и интенсивности отказов
и интенсивности отказов  ; построить их графики;
; построить их графики;
2) числовые характеристики: среднюю наработку до отказа 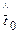 , дисперсию наработки до отказа
, дисперсию наработки до отказа 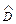 и ее среднее квадратическое отклонение
и ее среднее квадратическое отклонение  ;
;
3) закон распределения наработки до отказа.
Дано: 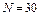 ,
, 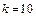 ,
,  ч,
ч, 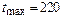 ч, интервал наработки: xt = 220 – 20 = 200 ч, шаг на интервале:
ч, интервал наработки: xt = 220 – 20 = 200 ч, шаг на интервале:  ч.
ч.
Найти: 1) 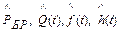 ; 2)
; 2) 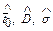 ; 3)
; 3) 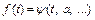 .
.
Решение: Сначала разбиваем рассматриваемую область полученных наработок до отказа на k = 10 участков (рис. 4.3).
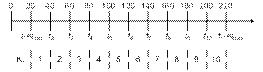
|
Рис. 4.3. Разделение интервала наработки 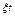 на k участков на k участков
|
Date: 2015-07-25; view: 957; Нарушение авторских прав