
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Множества. 1.1.1. Определение понятия «множество»
|
|
1.1.1. Определение понятия «множество»
Множество представляет собой некоторый набор определённых элементов, в общем случае неупорядоченных и не образующих последовательности. Множества могут иметь бесконечное и конечное число элементов или не иметь элементов вообще (бесконечное множество – натуральные числа; конечное множество – колода карт).
Множество записывается в следующем виде: А = { X1, X2, …, Xк, …, Xn }, где Хк – элемент множества А.
1.1.2. Соотношения между двумя множествами
Они зависят от того, имеют ли эти множества общие элементы.
Для двух множеств А и В существуют следующие возможности:
1) А и В имеют общие элементы, но каждое из множеств имеет также элементы, не принадлежащие другому множеству. Говорят, что множества пересекаются: А Ç В = С (рис. 1.1).
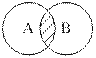
|
| Рис. 1.1. Диаграмма Вьенна при пересечении двух множеств |
2) А и В не имеют общих элементов (взаимоисключающие множества или непересекающиеся) (рис. 1.2).
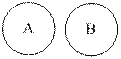
|
| Рис.1.2. Диаграмма Вьенна для непересекающихся множеств |
3) А целиком включает В (рис. 1.3).

|
| Рис. 1.3. Диаграмма Вьенна для случая, когда множество А целиком включает В |
В этом случае В является подмножеством А.
1.1.3. Операции с множествами
1) Объединение двух множеств – это множество С, которое содержит все элементы, принадлежащих ему множеств (рис. 1.4).
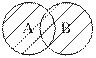
|
| Рис. 1.4. Диаграмма Вьенна при объединении двух множеств |
Математическая запись операции: А È В = С.
2) Пересечение двух множеств (А Ç В = С) – это множество С, которое содержит элементы, являющиеся общими для обоих множеств (рис. 1.5).
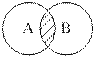
|
| Рис.1.5. Диаграмма Вьенна при пересечении двух множеств |
3) Разность двух множеств (А – В = С) – это множество С, состоящее из тех элементов А, которые не являются элементами множества В (рис. 1.6).

|
| Рис. 1.6. Диаграмма Вьенна при разности двух множеств |
Следует отметить, что А – В ¹ В – А.
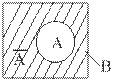
4) Дополнение множества А. Определим множество В как множество всех элементов, рассмотренных в данной ситуации (рис. 1.7). Дополнением множества А называется множество ` A, состоящее из элементов, которые не входят в множество А.
|
| Рис.1.7. Диаграмма Вьенна при разности двух множеств |
При этом ` A Ç A = 0 и ` A È A = B.
Date: 2015-07-25; view: 426; Нарушение авторских прав