Порядок выполнения работы. 1. Построение сетевого графика

1. Построение сетевого графика. Обозначим номером 1 событие начала всего проекта (исходное событие). Имеется две работы (a ₁ и a ₂), которые не имеют предшествующих работ. Следовательно, они начинаются с началом выполнения проекта. Изобразим их в виде дуг графа (стрелочек), выходящих из вершины 1 (исходного события). Над каждой дугой будем записывать наименование работы и в скобках ее продолжительность (рис. 3.3).

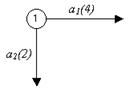
Рис. 3.3. Шаг 1 построения сетевого графика

Работе a ₃ предшествует работа a ₂. Это означает, что работа a ₂ должна закончится для того, чтобы могла начаться работа a ₃. Обозначим номером 2 событие окончания работы a ₂. Тогда на сетевом графике работа a ₃ выходит из события 2, т. е. следует непосредственно за дугой a ₂ (рис. 3.4).

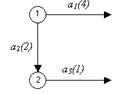
Рис. 3.4. Шаг 2 построения сетевого графика

Работе a ₄ предшествуют две работы: a ₁ и a ₃. Поэтому должно существовать событие, обозначающее факт окончания этих двух работ. Дуги a ₁ и a ₃ направим к одной вершине и обозначим ее следующим номером 3. Дуга a ₄ выходит из вершины 3. Таким образом, событие 3 обозначает факт окончания работ a ₁ и a ₃ и начала работы a ₄ (рис. 3.5).

Работе a ₅ предшествует работа a ₂. На графике уже имеется событие, обозначающее факт окончания этой работы (событие 2). Поэтому изобразим работу a ₅ в виде дуги, выходящей из вершины 2 (рис. 3.6).

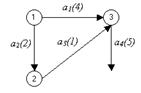
Рис. 3.5. Шаг 3 построения сетевого графика

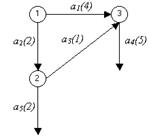
Рис. 3.6. Шаг 4 построения сетевого графика

Работе a ₆ предшествуют две работы: a ₄ и a _5. Поэтому направим дуги a ₄ и a ₅ к одной вершине и обозначим ее номером 4. Событие 4 обозначает факт окончания обеих работ a ₄ и a ₅ и начала работы a ₆ (рис. 3.7).

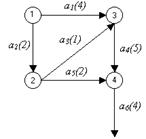
Рис. 3.7. Шаг 5 построения сетевого графика

Работе a ₇ предшествует работа a ₆. Обозначим событие окончания этой работы номером 5. Тогда дуга a ₇ выходит из этого события, т. е. непосредственно следует за дугой a ₆. Работе a ₈ предшествует работа a ₂. На сетевом графике уже имеется событие, обозначающее факт окончания работы a ₂. Это событие 2. Поэтому изобразим дугу a ₈ выходящей из вершины 2. Результат этих построений показан на рис. 3.8.

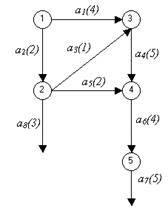
Рис. 3.8. Шаг 6 построения сетевого графика

Итак, на графике построены все работы, перечисленные в табл. 7.1. Поскольку сетевой график должен иметь только одно завершающее событие, дуги a ₇ и a ₈ направим к одной вершине, которой дадим номер 6. Эта вершина представляет собой факт завершения работ a ₇ и a ₈, а следовательно, и всего проекта (рис. 3.9).

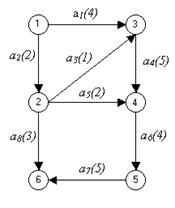
Рис. 3.9. Итоговый сетевой график примера

2. Определение критического пути в сетевом графике. Критический путь есть полный путь наибольшей продолжительности. Поэтому для его определения можно перебрать все полные пути в сетевом графике и выбрать тот, который имеет наибольшую продолжительность во времени. В нашем графике можно выделить следующие полные пути (обозначая их вершины):

m₁ = (1–2–3–4–5–6);

m₂ = (1–3–4–5–6);

m₃ = (1–2–4–5–6);

m₄ = (1–2–6).

Продолжительности этих полных путей следующие:

t (m₁) = 2 + 1 + 5 + 4 + 5 = 17;

t (m₂) = 4 + 5 + 4 + 5 = 18;

t (m₃) = 2 + 2 + 4 + 5=13;

t (m₄) = 2 + 3 = 5;

Таким образом, наибольшую продолжительность во времени, равную 18, имеет путь m₂, который и является критическим. Критический срок проекта равен 18 дней, т. е. это минимальный срок, за который будет выполнен проект. Однако такой способ определения критического пути в сетевом графике может быть использован только тогда, когда график является достаточно простым. В случае сложного графика, с большим количеством событий и работ, можно пропустить какой-либо полный путь и получить неверный результат. Способ, основанный на определении временных параметров событий и работ, излагаемый ниже, является более универсальным.

3. Расчет параметров событий сетевого графика. Выполним вычисления непосредственно на графике. Каждый кружок, изображающий событие, разделим на четыре сектора (рис. 3.10).

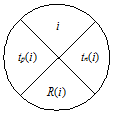
Рис. 3.10. Представление параметров события на сетевом графике

В верхнем секторе запишем номер события, в левом по мере вычислений будем записывать ранний срок t_р (i) свершения события i,
в правом – поздний срок t_п (i) этого события, а в нижнем – резерв времени R (i) события.

1. Определение ранних сроков свершения событий. Ранний срок свершения исходного события 1 по определению принимается за 0. Событие 2 наступит по окончании работы a ₂, которая начинается в момент времени 0 и продолжается 2 дня. Поэтому ранний срок свершения события 2 рассчитываем, как момент окончания этой работы:

.

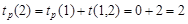Событие 3 есть факт окончания двух работ: a ₁ и a ₃. Работа a ₁ закончится в момент времени t_р (1) + t (1,3) = 0 + 4 = 4, а работа a ₃ закончится в момент t_р (2) + t (2,3) = 2 + 1 = 3. Поскольку событие 3 наступит тогда, когда обе работы a ₁ и a ₃ завершатся, нужно ориентироваться на ту работу, которая закончится позже, т. е.:

.

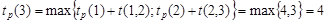Аналогично рассчитывается ранний срок свершения события 4, которое есть факт окончания работ a ₄ и a ₅:

.

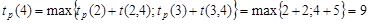Событие 5 наступит, когда закончится работа a ₆. Поэтому его ранний срок свершения

t_р (5) = t_р (4) + t (4,5) = 9 + 4 = 13.

Ранний срок свершения события 6, в которое входят две работы a ₇ и a ₈, рассчитывается аналогично событиям 3 и 4:

.

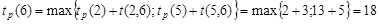Таким образом, при расчете раннего срока свершения события j нужно определить максимум величин t_p (i) + t (i, j) по всем входящим в соответствующую вершину дугам.

Результаты расчетов представлены в левых секторах событий на рис. 3.11. Ранний срок свершения завершающего события проекта есть критический срок проекта, т. е. минимальное время, в течение которого может быть завершен проект. В нашей задаче

t_кр = t_р (6) = 18.

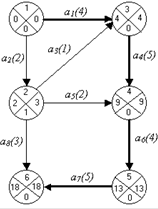
Рис. 3.11. Параметры событий сетевого графика

2. Определение поздних сроков свершения событий. Поздние сроки свершения событий рассчитываются “обратным ходом”, от завершающего события к исходному. Поздний срок свершения завершающего события 6 равен его раннему сроку свершения (или критическому сроку):

t_п (6) = t_р (6) = t_кр = 18.

Поздний срок свершения события 5 – это такой самый поздний срок, после которого остается ровно столько времени, сколько требуется для того, чтобы следующая за событием 5 работа a ₇ (выходящая из вершины 5 дуга) успела закончиться к критическому сроку. Чтобы эта работа, которая длится 5 дней, закончилась к 18 дню, она должна начаться на 13 день (18 – 5 = 13). Поэтому

t_п (5) = t_п (6) – t (5,6) = 18 – 5 = 13.

За событием 4 следует работа a ₆. Она должна закончится к 13 дню для того, чтобы следующая за ней работа успела к критическому сроку. Поэтому работа a ₆ должна начаться на 9 день (13 – 4 = 9). Таким образом,

t_п (4) = t_п (4) – t (4,5) = 13 – 4 = 9.

Аналогично для события 3, которым начинается одна работа a ₄:

t_п (3) = t_п (3) – t (3,4) = 9 – 5 = 4.

Событием 2 начинаются сразу три работы a ₃, a ₅ и a ₈ (дуги, выходящие из вершины 2). Для событий 3, 4 и 6, означающих соответствующие моменты окончания этих работ, поздние сроки свершения уже рассчитаны. Поэтому работа a ₃ должна начаться не позднее
t_п (3) – t (2,3) = 4 – 1 = 3 дня, работа a ₅ – не позднее t_п (4) – t (2,4) = 9 –
– 2 = 7 дня, а работа a ₈ – не позднее t_п (6) – t (2,6) = 18 – 3 = 15 дня. Чтобы удовлетворить эти требования для всех трех работ, нужно ориентироваться на минимальный из этих сроков. Поэтому

t_п (2) = min (3;7;15) = 3.

Таким образом, при расчете позднего срока свершения события i нужно брать минимум величин t_п (j) – t (i, j) по всем исходящим из данной вершины дугам.

Аналогично для события 1:

.

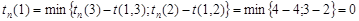При правильных расчетах поздний срок исходного события должен получиться равным 0, а поздний срок свершения события никогда не должен быть меньше раннего.

Результаты расчетов показаны на графике в правых секторах событий (см. рис. 3.11).

3. Определение резервов времени событий. Резерв времени события определяется как разность между поздним и ранним сроками свершения этого события:

R (1) = t_n (1) – t_p (1) = 1 – 1 = 0;

R (2) = t_n (2) – t_p (2) = 3 – 2 = 1 и т. д.

Резервы времени событий показаны в нижних секторах событий на рис. 3.11.

4. Определение критического пути на основании временных параметров событий. Как известно, критические события не имеют резерва времени. Поэтому критический путь пройдет по событиям 1, 3, 4, 5, 6. Сумма продолжительности критических работ должна быть равна критическому сроку проекта. Проверим это:

t (1,3) + t (3,4) + t (4,5) + t (5,6) = 4 + 5 + 4 + 5 = 18 = t_кр.

Критический путь выделен на сетевом графике.

5. Определение параметров работ. Критические работы, как и критические события, резервов времени не имеют. Поэтому будем рассматривать только некритические работы. Расчеты полного резерва времени и других параметров для некритических работ приведены в табл. 3.2.

Таблица 3.2. Параметры нектритических работ примера

Работа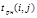
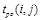
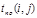
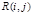
(1,2)
(2,3)
(2,4)
(2,6)

Ранний срок начала работы совпадает с ранним сроком свершения начального события работы:

t_рн (1,2) = t_p (1) = 0;

t_рн (2,3) = t_p (2) = 2 и т. д.

Ранний срок окончания работы рассчитывается как сумма раннего срока начала и продолжительности работы:

t_рo (1,2) = t_pн (1,2) + t (1,2)= 0 + 2 = 2;

t_рo (2,3) = t_pн (2,2) + t (2,3)= 2 + 1 = 3 и т. д.

Поздний срок окончания работы совпадает с поздним сроком свершения конечного события работы:

t_no (1,2) = t_n (2) = 3;

t_no (2,3) = t_n (3) = 4 и т. д.

Резерв времени работы равен разности между поздним и ранним сроками ее окончания:

R (1,2) = t_no (1,2) – t_po (1,2) = 3 – 2 = 1;

R (2,3) = t_no (2,3) – t_po (2,3) = 4 – 3 = 1 и т. д.

Итак, данный проект может быть выполнен за 18 дней. При этом работы a ₁, a ₄, a ₆ и a ₇ являются критическими, т. е. должны быть выполнены точно в срок. Работы a ₂, a ₃, a ₅ и a ₈ имеют резервы времени, т. е. они могут быть начаты позже или выполняться дольше, чем их объявленная продолжительность, на величину этого резерва. При этом срок выполнения всего проекта не изменится.

Date: 2015-07-25; view: 627; Нарушение авторских прав