Основные теоретические сведения. Можно выделить две основные постановки задачи оптимизации сетевого графика:

Можно выделить две основные постановки задачи оптимизации сетевого графика:

1. Минимизация времени выполнения проекта при заданных ресурсах:

F = t_кр ® min,

r £ r^выд,

где r – требуемые ресурсы;

r^выд – выделенные ресурсы.

2. Минимизация требуемых ресурсов, обеспечивающих выполнение проекта в заданный период времени:

F = r ® min,

t_кр £ t^зад.

Рассмотрим задачу 1 (минимизация времени выполнения проекта). Сокращение времени выполнения работ может быть достигнуто за счет вложения в них некоторых ресурсов. Такими ресурсами являются, например, трудовые ресурсы или машины, а также универсальный ресурс – финансы. При вложении дополнительного количества финансов в работу сокращение ее длительности достигается за счет:

а) найма дополнительного количества рабочих;

б) улучшения организации работ;

в) автоматизации производственных процессов;

г) применения передовых технологий и т. д.

Далее в качестве ресурса будем рассматривать только финансы. При этом будем считать, что каждая работа a_i характеризуется некоторой трудоемкостью Q_i, а время выполнения работы t_i обратно пропорционально величине вложенных в нее финансов r_i:

,

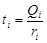
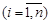где n – количество работ проекта.

Однако насыщение любой работы финансами не беспредельно. Для каждой работы существует минимально возможное время ее выполнения, которое определяется технологическими особенностями этой работы:

,

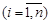где d_i – минимально возможное время выполнения работы.

Критический срок проекта зависит как от длительностей работ этого проекта t_i, так и от логической последовательности и взаимозависимости работ. Обозначим: L – логическая зависимость работ. Тогда критический срок проекта можно представить в виде функции:

t_кр = f (L, t ₁, t ₂, …, t_n).

Функция f чаще всего не имеет конкретного математического вида, но легко может быть задана в приложении MS Excel с помощью цепочки ссылок и простейших функций.

Сокращение времени выполнения проекта возможно как за счет внутренних резервов, так и внешних дополнительных средств. В первом случае у работ, имеющих резервы времени, забирают ресурсы и передают их работам, лежащим на критическом пути. Это позволяет сократить длительность критических работ. В случае использования внешних дополнительных средств, их также стараются вложить сначала в критические работы. Однако критический путь при этом может измениться и дальнейшее вложение ресурсов в те же работы станет неэффективным. Поэтому задача оптимизации как внутренних резервов, так и внешних дополнительных средств не является тривиальной. Для ее эффективного решения необходимо составить задачу математического программирования и решить ее на ЭВМ.

Оптимальный план перераспределения финансов является решением следующей задачи нелинейного программирования:

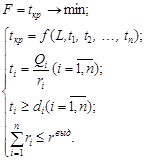(3.8)

Если r^выд – это то же количество ресурсов, что планировалось вначале, то имеем задачу отыскания внутренних резервов. Если же 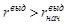, то это задача оптимизации вложения дополнительных средств.

Date: 2015-07-25; view: 416; Нарушение авторских прав