Сетевой график и правила его построения

Метод сетевого планирования и управления используется при планировании сложных комплексов взаимосвязанных работ. Анализ сетевой модели позволяет:

· четко выявить взаимосвязь различных этапов проекта, условия начала тех или иных работ;

· определить срок выполнения проекта;

· выявить возможности задержки начала каждой работы или удлинения срока ее выполнения;

· оптимизировать время выполнения проекта или ресурсы, требуемые для его выполнения.

Основой метода сетевого планирования является сетевой график – графическая модель некоторого комплекса взаимосвязанных работ (проекта или производственного процесса). Сетевой график отражает логическую взаимосвязь и взаимообусловленность входящих в него работ. С математической точки зрения сетевой график представляет собой ориентированный граф без контуров, дугам которого приписаны некоторые числовые значения.

Дугам графа соответствуют работы. Работой называется любой процесс, происходящий во времени. Различают три вида работ:

Действительная работа (¾¾¾®) – это любой трудовой процесс, требующий ресурсов и имеющий некоторую продолжительность (разработка проекта, подвоз материалов, монтаж оборудования и т. д.)

Ожидание (¾ × ¾ ×®) – это процесс, не требующий ресурсов, но имеющий некоторую продолжительность (затвердение бетона, сушка штукатурки, рост растений и т. д.)

Фиктивная работа (¾ ¾ ®) отражает логическую зависимость между действительными работами. Не требует ресурсов и имеет нулевую продолжительность.

Над дугой может быть указана числовая характеристика работы (например, время ее выполнения).

Вершинам графа соответствуют события. Событие означает факт окончания всех работ, в него входящих, и начала всех работ, из него исходящих. Событие не имеет продолжительности и не потребляет ресурсов. Событие в сетевом графике имеет номер. Событие, с которого начинается выполнение проекта, называется исходным и обозначается I. Исходное событие не имеет предшествующих работ. Событие, которое констатирует факт завершения проекта, называется завершающим и обозначается S. Завершающее событие не имеет последующих работ.

Работа может обозначаться двумя способами:

1. Парой номеров (i, j), где i – номер начального события работы,
j – номер конечного события работы;

2. Буквенно-числовым обозначением с номером работы: a ₁, b ₂ и т. д.

Продолжительность работы обозначается t (i, j).

При построении сетевых графиков необходимо соблюдать следующие правила:

1. В сетевом графике не должно быть событий (кроме исходного), в которые не входит ни одна дуга.

2. Не должно быть событий (кроме завершающего), из которых не выходит ни одной дуги.

3. Сетевой график не должен содержать контуров.

4. Любая пара событий сетевого графика может быть соединена не более чем одной дугой. Если нужно изобразить параллельно выполняемые работы с общими начальными и конечными событиями, то рекомендуется ввести дополнительные события и соединить их с последующими фиктивными работами. Пусть, например, имеются три различные работы a ₁, a ₂ и a ₃, которые начинаются одним событием 2 и заканчиваются одним событием 5 (рис. 3.1). В этой ситуации может возникнуть путаница из-за того, что различные работы имеют одно и то же обозначение (2,5). Чтобы избежать этого, введем фиктивные работы, как показано на рис. 3.2.

5. События должны быть пронумерованы так, чтобы для любой работы (i, j) номер конечного события был больше номера начального (j > i).

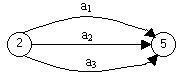
Рис. 3.1. Фрагмент неверного сетевого графика

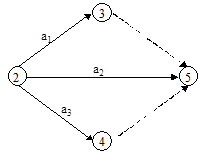
Рис. 3.2. Правильное изображение параллельных работ

Date: 2015-07-25; view: 448; Нарушение авторских прав