
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Порядок выполнения работы. 1. Ввод исходных данных задачи.В ячейки A1 и B1 ввести заголовки исходных данных, в ячейки A2:A9 – номера месяцев
|
|
1. Ввод исходных данных задачи. В ячейки A1 и B1 ввести заголовки исходных данных, в ячейки A2:A9 – номера месяцев, а в ячейки B2:B9 – фактические данные по количеству брака (рис. 2.16).
2. Подготовка экрана Excel для запуска надстройки Поиск решения. Ячейки A13:B13 отведем для неизвестных пока коэффициентов тренда a и b. Снабдим их соответствующими заголовками, обведем рамочкой и зададим в них начальные значения параметров (например, нулевые).
В ячейки C2:C9 нужно записать теоретические значения показателя, т. е. рассчитанные по формуле (2.6) для каждого месяца. При этом в качестве параметров a и b нужно использовать содержимое ячеек A13 и B13. Введем в ячейку C2 формулу =$A$13+$B$13/A2. Скопируем эту формулу с помощью автозаполнения в ячейки C3:C9.

Рис. 2.16. Исходные данные и подготовка информации для Поиска решения
В ячейке C11 запишем формулу суммы квадратов разностей (2.3). Для этого можно использовать специальную функцию Excel СУММКВРАЗН(), аргументами которой являются диапазоны фактических (B2:B9) и теоретических (С2:C9) значений экономического показателя. Для ввода этой функции можно использовать мастер функций. Вид листа Excel в режиме представления формул показан на рис. 2.17.
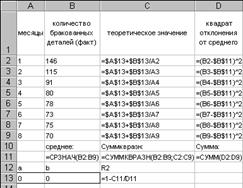
Рис. 2.17. Исходные данные задачи в режиме представления формул
Кроме определения параметров тренда, в задаче следует рассчитать коэффициент детерминации модели по формуле (2.4). Этот показатель характеризует точность модели, т. е. насколько хорошо модель описывает имеющиеся фактические данные.
Введем в ячейку B11 формулу вычисления среднего значения уровней ряда
=СРЗНАЧ(B2:B9).
В столбце D рассчитаем квадрат отклонения фактического значения показателя от его среднего значения. Для этого в ячейку D2 введем формулу
=(B2-$B$11)^2.
Скопируем данную формулу с помощью автозаполнения в ячейки D3:D9.
В ячейке D11 подсчитаем сумму этих величин с помощью следующей формулы:
=СУММ(D2:D9).
Таким образом, в ячейке D11 мы получаем знаменатель дроби из формулы (2.5):
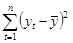 .
.
Величину коэффициента детерминации по формуле (2.4) рассчитаем в ячейке C13:
=1–C11/D11.
После определения оптимальных параметров тренда число в этой ячейке будет характеризовать точность найденной модели.
3. Определение параметров тренда с помощью надстройки Поиск решения.
Вызовем надстройку Поиск решения командой Сервис / Поиск решения ….
Окно Поиск решения заполним как показано на рис. 2.18. Целевой ячейкой является ячейка C11, содержащая формулу суммы квадратов разностей фактического и теоретического значений.
Следует подобрать такие значения параметров тренда в ячейках A13:B13, чтобы ячейка C11 была минимальной. Ограничений в этой задаче нет. Параметры изменять не нужно.
Нажатие кнопки Выполнить активизирует процесс поиска решения, результатом которого являются значения параметров a и b, показанные на рис. 2.19.
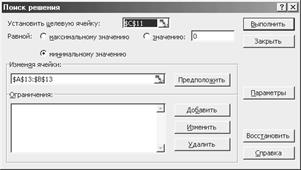
Рис. 2.18. Окно Поиск решения для решения задачи определения
параметров тренда
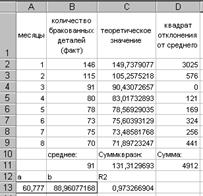
Рис. 2.19. Результаты решения задачи определения параметров
обратного тренда
Таким образом, уравнение тренда имеет следующий вид:
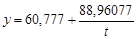 .
.
Коэффициент детерминации для этой модели равен R 2 = 0,9733.
Это довольно хороший показатель, который позволяет надеяться на достоверность прогноза.
4. Построение графика фактических значений и линии тренда. Для наглядного представления модели построим графики фактических значений и кривой роста. Очевидно, что значения в столбце C рассчитаны на основании уравнения тренда и поэтому принадлежат на графике кривой роста. Выделим диапазон A1:C9, вызовем мастер диаграмм нажатием кнопки  на панели инструментов, и построим диаграмму типа точечная как показано на рис. 2.20.
на панели инструментов, и построим диаграмму типа точечная как показано на рис. 2.20.
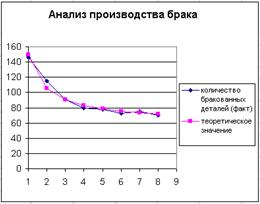
Рис. 2.20. График фактических значений количества брака и кривая роста
5. Выполнение прогнозов. Для того, чтобы сделать прогноз, нужно подставить в уравнение тренда значение момента времени, относящееся к будущему.
Введем в ячейки A15 и A16 номера следующих двух месяцев (9 и 10). В соответствующие ячейки столбца С запишем формулы расчета по линии тренда, т. е. в ячейку С15 введем формулу
=$A$13+$B$13/A15.
Скопируем данную формулу в ячейку С16. Результат вычисления по этим формулам показан на рис. 2.21. Таким образом, прогноз количества бракованных деталей на 9-й месяц составляет примерно 71 деталь, а на 10-й месяц – примерно 70 деталей.

Рис. 2.21. Прогнозы по найденной модели
Добавим эти прогнозы на график кривой роста. Для этого выделим ячейки C15:C16 и скопируем их в буфер обмена. Затем выполним щелчок мышью по графику и вставим данные из буфера. В результате график кривой роста будет продолжен вперед на два месяца (рис. 2.22).
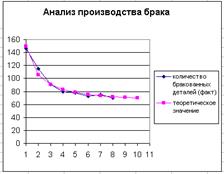
Рис. 2.22. Иллюстрация прогнозов по линии тренда на графике
5.3. Задания для самостоятельной работы*
Вариант 1. В табл. 2.21 приведены данные об объеме продаж фирмы, торгующей подержанными автомобилями, в течение 12 недель ее работы. С помощью надстройки Поиск решения определить параметры тренда вида: y = at 2 + (b / t). Оценить точность этой модели. Сделать прогноз на две недели вперед.
Таблица 2.21. Данные об объеме продаж подержанных автомобилей
| Неделя | 1-я | 2-я | 3-я | 4-я | 5-я | 6-я | 7-я | 8-я | 9-я | 10-я | 11-я | 12-я |
| Количество проданных единиц |
Ответ: a = 1,95, b = 9,94, R 2 = 0,9844.
Вариант 2. Имеются данные об объеме продаж некоторой фирмы (табл. 2.22). С помощью надстройки Поиск решения определить параметры простой экспоненциальной модели. Оценить точность этой модели. Сделать прогноз на две недели вперед. (Учтите, что начальное приближение для параметра b следует задавать числом, отличным от нуля, например равным единице).
Таблица 2.22. Данные об объеме продаж
| Неделя | 1-я | 2-я | 3-я | 4-я | 5-я | 6-я | 7-я | 8-я | 9-я | 10-я | 11-я | 12-я |
| Количество проданных единиц |
Ответ: a = 30,070, b = 1,074, R 2 = 0,948.
Вариант 3. Себестоимость некоторой продукции снижается каждый месяц, как показано в табл. 2.23. Определите параметры тренда
y = at + (b / t) + с и оцените точность этой модели. Сделайте прогноз на 2 месяца вперед.
Таблица 2.23. Снижение себестоимости
| Месяц | 1-й | 2-й | 3-й | 4-й | 5-й | 6-й | 7-й | 8-й | 9-й |
| Себестоимость продукции, усл. ед. |
Ответ: a = –2,108, b = 9,5264, c = 54,2760, R 2 = 0,9291.
Вариант 4. В табл. 2.24 приведены статистические данные о продаже алкогольных напитков на душу населения в Республике Беларусь. Предположив в качестве тренда полином второй степени, определите его параметры с помощью надстройки Поиск решения. Оцените точность этой модели. Сделайте прогноз о продаже алкоголя на 2003 г. (при решении рекомендуется ввести номера временных периодов: 1, 2, …).
Таблица 2.24. Статистические данные о продаже алкогольных напитков
| Годы | |||||||
| Количество алкоголя, л | 6,7 | 7,4 | 7,8 | 8,9 | 9,7 | 8,8 | 8,8 |
Ответ: a 0 = 5,2143, a 1 = 1,4024, a 2 = –0,1262, R 2 = 0,8787.
Вариант 5. В табл. 2.25 приведены статистические данные о численности безработных в Республике Беларусь, зарегистрированных органами государственной службы занятости на конец каждого года (тыс. чел.). С помощью надстройки Поиск решения определить параметры и коэффициент детерминации для обратного тренда вида (2.6). Сделать прогноз на два года вперед (при решении рекомендуется ввести номера временных периодов: 1,2, …).
Таблица 2.25. Статистические данные о численности безработных
в Республике Беларусь
| Годы | ||||||
| Количество безработных | 182,5 | 126,2 | 105,9 | 95,4 | 95,8 | 102,9 |
Ответ: a = 75,1401, b = 105,2484, R 2 = 0,9702.
Вариант 6. Динамика розничного товарооборота торговой фирмы приведена в табл. 2.26 (в процентах к 1990 г.). Определить параметры тренда вида y = a 0 + a 1 t + (a 2 / t). Оценить точность этой модели. Сделать прогноз на два года вперед (при решении рекомендуется ввести номера временных периодов: 1, 2, …).
Таблица 2.26. Динамика розничного товарооборота торговой фирмы,
% к 1990 г.
| Годы | ||||||||||
| Товарооборот |
Ответ: a 0= –16,2357, a 1 = 12,5028, a 2 = 105,7374, R 2 = 0,9735.
Вариант 7. Имеются данные об объеме продаж некоторой фирмы (табл. 2.27). С помощью надстройки Поиск решения определить параметры простой экспоненциальной модели. Оценить точность этой модели. Сделать прогноз на 2 месяца вперед. (Учтите, что начальное приближение для параметра b следует задавать равным числу, отличному от нуля, например, единице).
Таблица 2.27. Данные об объеме продаж, р.
| Месяц | 1-й | 2-й | 3-й | 4-й | 5-й | 6-й | 7-й | 8-й | 9-й | 10-й |
| Объем продаж |
Ответ: a = 88,0719, b = 1,0834, R 2 = 0,9752.
Вариант 8. Динамика числа продаж некоторой фирмы, торгующей бытовой техникой, приведена ниже в табл. 2.28. Используя надстройку Поиск решения, определить параметры полинома второй степени. Оценить точность модели. Сделать прогноз на 3 месяца вперед.
Таблица 2.28. Динамика числа продаж
| Месяц | 1-й | 2-й | 3-й | 4-й | 5-й | 6-й | 7-й | 8-й | 9-й |
| Количество проданных единиц |
Ответ: a 2 = 3,8755, a 1 = 11,6947, a 0 = 18,6905, R 2 = 0,9925.
Контрольные вопросы
1. Каковы этапы решения задачи прогнозирования на основе трендовой модели?
2. В чем суть и назначение метода наименьших квадратов?
3. Для чего рассчитывается коэффициент детерминации R 2?
4. Как выполняется прогноз на основе трендовой модели?
5. В чем преимущества использования надстройки Поиск решения для реализации метода наименьших квадратов?
6. Какие стандартные функции Excel используются в данной работе?
Лабораторная работа 6.
Использование встроенных функций Excel
в задачах прогнозирования
Date: 2015-07-25; view: 703; Нарушение авторских прав