Порядок выполнения работы. 1. Подготовка таблиц.На рабочем листе MS Excel заведем две таблицы, в которых мы будем рассчитывать параметры событий (рис

1. Подготовка таблиц. На рабочем листе MS Excel заведем
две таблицы, в которых мы будем рассчитывать параметры событий
(рис. 3.13) и параметры работ (рис. 3.14).

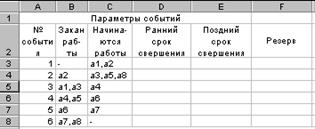
Рис. 3.13. Таблица для расчета параметров событий

В первой таблице для каждого события укажем работы, для которых это событие является конечным (столбец B). В столбце C перечислим работы, для которых это событие является начальным. Таким образом, будет задана логическая последовательность работ данного сетевого графика. Во второй таблице для каждой работы укажем шифр (номер начального события и номер конечного события), а также ее длительность.

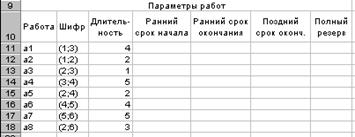
Рис. 3.14. Таблица для расчета параметров работ

2. Определение параметров событий и работ. Сначала рассчитаем параметры событий. На рис. 3.15. показана таблица в режиме представления формул.

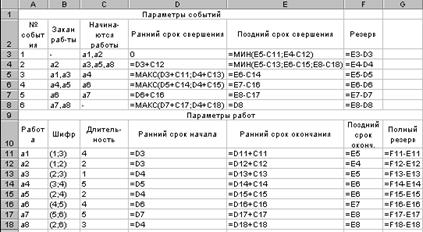
Рис. 3.15. Расчеты параметров событий и работ

При расчете раннего срока свершения события воспользуемся следующими правилами:

· вычисления производятся последовательно от исходного события до завершающего;

· ранний срок свершения исходного события равен нулю: D3=0;

· если событием заканчивается только одна работа, то ранний срок свершения события равен сумме раннего срока свершения начального события этой работы и ее длительности: D4=D3+C12 и т. д.;

· если событием заканчиваются несколько работ, то нужно найти максимум этих сумм по всем входящим в событие работам:

D5=МАКС(D3+C11;D4+C13);

D6=МАКС(D5+C14;D4+C15) и т. д.

При вычислении позднего срока свершения события следует придерживаться следующих правил:

· расчеты выполняются в обратном порядке, от завершающего события к исходному.

· поздний срок свершения завершающего события равен его раннему сроку свершения: E8=D8;

· если событием начинается только одна работа, то его поздний срок свершения равен разности между поздним сроком конечного события этой работы и ее длительностью: E7=E8–C17, E6=E7–C16 и т. д.;

· если событием начинается несколько работ, то его поздний срок свершения вычисляется как минимум этих разностей по всем исходящим работам: E4=МИН(E5–C13;E6–C15;E8–C18); E3=МИН(Е5–С11; Е4–С12).

Резерв времени события вычисляется как разность позднего и раннего срока свершения события.

Параметры работ вычисляются на основании параметров событий.

Ранний срок начала работы равен раннему сроку свершения того события, которым работа начинается: D11=D3 и т. д.

Ранний срок окончания работы вычисляется как сумма раннего срока начала работы и ее длительности: E11=D11+C11 и т. д.

Поздний срок окончания работы равен позднему сроку свершения события, которым работа заканчивается: F11=E5 и т. д.

Полный резерв времени работы вычисляется как разность позднего и раннего срока окончания работы: G11=F11-E11 и т. д.

Результаты расчетов параметров работ приведены на рис. 3.16.

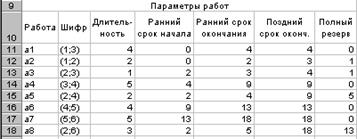
Рис. 3.16. Результаты расчетов параметров работ

После определения резервов времени работ становится ясно, какие работы принадлежат критическому пути. Резервы времени критических работ равны нулю. Работы критического пути должны следовать друг за другом (составлять полный путь). Очевидно, что в нашей задаче критическому пути принадлежат работы a ₁, a ₄, a ₆ и a ₇. Таким образом, до выполнения оптимизации критический путь следующий: 1 ® 3 ® 4 ® 5 ® 6.

3. Подготовка данных для построения линейного графика. В принципе все необходимые для построения линейного графика работ данные уже нами получены. Для удобства построений сведем эти данные вместе (рис. 3.17).

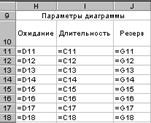
Рис. 3.17. Подготовка данных для линейной диаграммы

Столбец Ожидание будет показывать время, на которое отложено начало работы относительно начала всего проекта. В этот столбец перенесем данные столбца Ранний срок начала работы.

Столбец Длительность равен длительности работы, т. е. представляет собой копию столбца С.

Столбец Резерв показывает, на какое время можно отложить начало работы или увеличить ее длительность. Этот столбец представляет собой копию столбца G.

4. Построение линейного графика. Выделим несмежные диапазоны с шифрами работ (в нашем случае B10:B18) и параметрами диаграммы (H10:J18).С помощью Мастера диаграмм построим линейный график работ как показано на рис. 3.18. Следует выбрать тип диаграммы Линейчатая с накоплением.

Рис. 3.18. Линейный график работ

5. Подготовка исходных данных для задачи оптимизации внутренних резервов. В столбцы K и L занесем заданные в условии величины трудоемкости работ и выделенных для каждой работы ресурсов (рис. 3.19). В ячейку L20 занесем формулу суммы всех ресурсов, требуемых под данный проект: СУММ(L11:L18). В ячейку L21 запишем число, равное количеству выделенных ресурсов, которое необходимо распределить между работами. Поскольку решается сначала задача оптимизации внутренних резервов, в ячейке L21 будет та же величина, что получена в ячейке L20 (в нашем случае – 80).

Изменим столбец С, записав вместо чисел формулы расчета длительностей работ: C11=K11/L11, C12=K12/L12 и т. д.

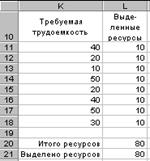
Рис. 3.19. Исходные данные по трудоемкости и ресурсам

6. Решение задачи оптимизации длительности проекта с помощью надстройки Поиск решения. Задача оптимизации длительности проекта может быть записана в виде формулы (3.8). При этом предполагается, что длительность любой работы не может быть меньше 1, т. е. d_i = 1 .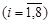

Окно надстройки Поиск решения для данной задачи нелинейного программирования показано на рис. 3.20. В окне Параметры флажок Линейная модель устанавливать не нужно.

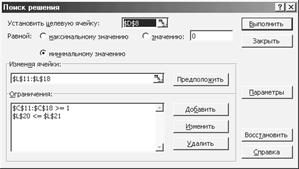
Рис. 3.20. Окно Поиск решения для задачи оптимизации критического срока проекта

После нажатия кнопки Выполнить надстройка Поиск решения находит наилучший результат перераспределения ресурсов между работами (рис. 3.21).

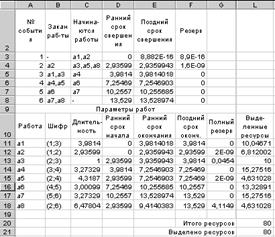
Рис. 3.21. Результаты оптимизации внутренних резервов

Date: 2015-07-25; view: 553; Нарушение авторских прав