Приведены в пример практические реализации В.Я. Ротыча

Идентификация регулирующего канала объекта – рис.3.3 а

Идентификация канала действия некоторого возмущения λ(t) – рис.3.3 б

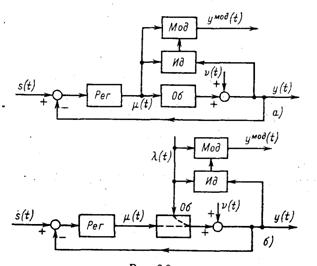
Рисунок 7 -

Разомкнутая система с компенсацией возмущения λ(t) – рис.3.4

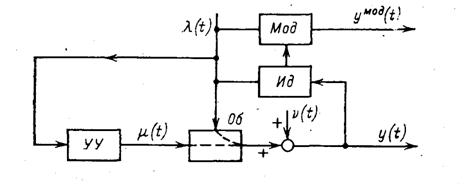
Рисунок 8 -

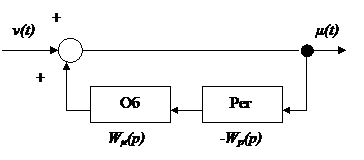
μ(t) - регулирующее воздействие

ν(t) -неконтролируемое возмущение

y(t) -выходной сигнал объекта

y^мод(t) -выходной сигнал модели

λ(t) – некоторое возмущение

s(t) – регулирующее воздействие на всю систему

Об - объект

Рег - регулятор

Ид - идентифицирующее устройство

Мод - модель объекта

1) Идентификация регулирующего канала объекта (рисунок 3.3а)

S(t)= 0

a) Входы неконтролируемы, а μ(t) - это одна из возможных величин системы регулирования. При известной модели регулирования μ(t) не надо контролировать, она связана с контролируемой величиной y(t).x(t)=μ(t)

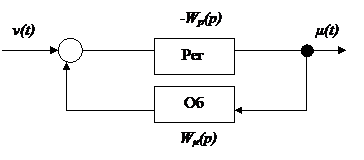
W_μ(p) – оператор регулирующего канала объекта;

W_p(p) – оператор регулятора;

p – оператор Лапласа.

W_пр(p) – передаточная функция прямого канала;

W_ос(p) – передаточная функция обратного канала связи;

W(p) – передаточная функция всей системы;

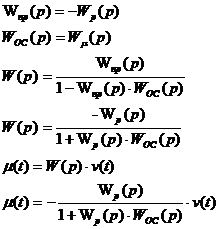
б)

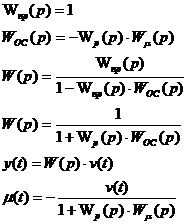
2)

Подставим (2) в (1):

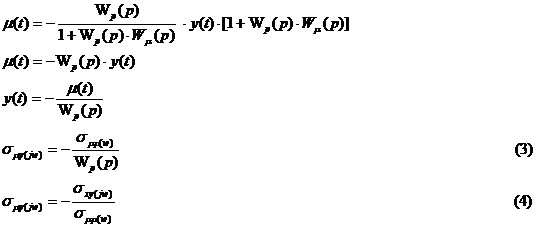
W_(jw) – комплексная частотная характеристика объекта (изображение по Фурье его импульсной характеристики)

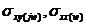- изображение по Фурье – спектром сигналов.

Подставим (3) в (4):

3) Идентификация канала действия некоторого возмущения λ(t) (рисунок 3.3б)

x(t)=μ(t)

а) Вход и выход контролируются, характеристика зависит от неизвестных операторов W_μ(p) и W_λ(p).

v(t)= 0

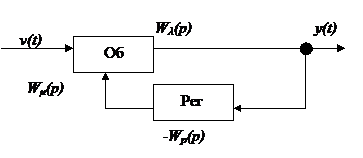
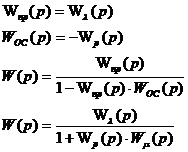
б) λ(t) =0

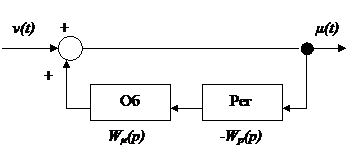
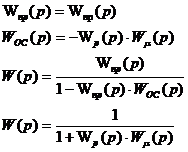
в)

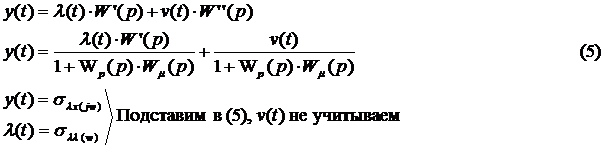
Подставим (6) в (4):

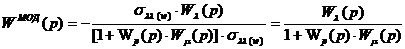
Вывод:

В первом случае (3.3а) мы ожидали получить W_μ(p), а получили 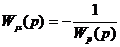. Во втором и третьем случае нужно было оценить W_λ(p), но получили оценку для системы в целом. Объект – это часть системы, поэтому необходимо оперировать с воздействиями, являющимися входными сигналами всей системы. Входной сигнал следует выбирать так, чтобы идентифицируемый канал системы зависли только от одного неизвестного оператора.

4) Разомкнутая система с компенсацией возмущения λ(t) (рисунок 3.4)

x(t)=λ(t); v(t)= 0;

Вход и выход контролируются.

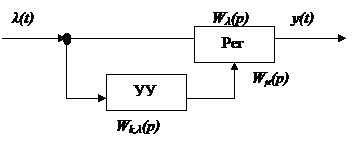
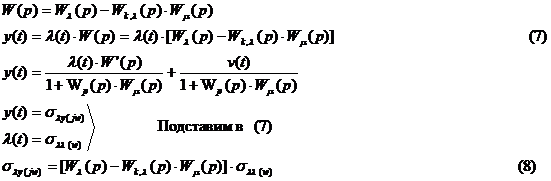
Подставим (8) в (4):

Вывод:

Если мы будем рассматривать объект отдельно от всей системы, то получим вышеуказанные зависимости (нежелательные). Необходимо рассматривать объект как часть системы, а не обособленно.

Идентификация регулирующего канала может оказаться выполнимой только в том случае, когда среди действующих на объект возмущений имеется хотя бы одно доступное для контроля (прямого или косвенного) возмущение, идущее по одному каналу с регулирующим воздействием.

Условия проведения пассивного метода идентификации:

1) Случайные помехи, искажающие реакцию на выбранное входное воздействие, должны быть независимыми от этого воздействия (в противном случае в состав погрешности оценки динамической характеристики, помимо случайной составляющей, которая может быть сведена к допустимо малой величине с помощью методов математической статистики, будет входить также и неустранимая систематическая погрешность). Другими словами, не должно быть корреляции между входной величиной и случайной помехой.

2) Входное воздействие, по которому осуществляется идентификация, должно обладать достаточно широким частотным спектром, во всяком случае, не меньшем, чем полоса частот, в пределах которой требуется оценить динамическую характеристику системы.

По данным пассивного эксперимента в большинстве случаев невозможно найти искомую модель. Рассмотрим в качестве примера модель следующего вида:

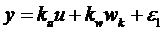, (44)

ε ₁ – эффекты влияния неучтенных факторов.

При этом объект исследования является объектом управления. Если система управления не обладает динамикой, то ошибка управления ε будет полностью совпадать ε_1, поэтому, что 1 и 2 случай эта ошибка будет вызвана влиянием возмущений W_н, если же система контролирования, то будет динамической и ошибка управления ε₂ не будет равна ε₁. Появится дополнительная ошибка ε₂= ε₁+ δε, где δε = динамические ошибки.

Но величина этой ошибки существенно меньше, чем ε₁, т.е. что для нединамической системы ε₁ соответствует уравнению 44 и будет совпадать с ошибкой уравнения и в этом случае уравнение воздействия на y и будет функция связана с эффектом неучтенных факторов ε_1.

В случае динамической системы ошибка регулирования ε₂, по тем меньше статической связи между эффектами учтенные и неучтенные факторов.

Принцип выбора объекта исследования (ОИ):

При выборе ОИ необходимо так отделять ее от окружающей среды, чтобы разрыв был при очень слабой связи или при их отсутствии (т.е. те, что остались за пределами связи). Предполагается отсутствие связи между u(t) и ε(t). ОИ должен быть системой, а не объектом.

Пусть стоит задача оценивания значений коэффициентов k_u этого уравнения, т.е. задача нахождения коэффициентов передачи по регулирующему каналу объекта методом наименьших квадратов.

Оператор математического ожидания можно заменить средним арифметическим. Для простоты дальнейших рассуждений будем считать, что ε, y и u есть случайные величины с нулевым математическим ожиданием.

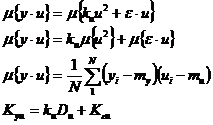
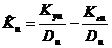(45)

Метод наименьших квадратов (МНК) дает формулу:

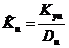(46)

Формулы (45) и (46) равны, если отсутствует корреляция между ε и u. Согласно пятой предпосылке МНК, K_εu должно быть равно 0, тогда формулы будут равны и соответственно оценка коэффициента передачи K_u будет несмещенной.

Однако: при использовании данных пассивного эксперимента в силу существования достаточно тесных связей между ε и u это условие никогда не будет выполняться и полученная оценка коэффициента передачи будет всегда заниженной.

В частности, при 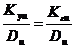мы получи значение оценки 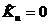, а в случае 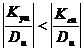коэффициент будет с обратным по отношению к действительности знаком. При эксперименте необходимо охватить как можно больший диапазон значений и K_εu приравнять к нулю.

Случайная величина (СВ) – это величина, которая в результате испытания принимает одно из возможных числовых значений, наперед неизвестное и зависящее от случайных причин, которые не могут быть учтены. СВ – это понятие модельное.

Закон распределения СВ – это соответствие между значениями случайной величины и вероятностными значениями.

Свойства функции распределения СВ:

5) функция распределения f(x) есть неубывающая функция аргумента F(x ₂ )≥F(x ₁ );

6) на -∞ функция распределения равна 0;

7) на +∞ функция распределения равна 1;

Математическое ожидание – это сумма произведений значений случайной величины на вероятности значений

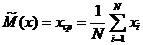
Дисперсия СВ – это математическое ожидание квадрата отклонения значений СВ от ее математического ожидания

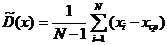
Коэффициент ковариации (ковариационный момент) - это характеристика линейной взаимосвязи между двумя центрированными СВ (коэффициент взаимной ковариации) или различными отсчетами одной СВ

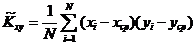
Коэффициент корреляции - это числовая характеристика степени тесноты линейной взаимосвязи двух нормированных СВ.

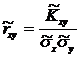
Стационарные процессы – это случайные процессы, протекающие во времени, приблизительно однородны, имеющие вид непрерывных случайных колебаний вокруг некоторого значения, причем ни средняя амплитуда, ни характер этих колебаний не обнаруживают существенных изменений с течением времени.

2.2. Активный эксперимент – это такой эксперимент, такой способ для получения экспериментальных данных, при котором исследователь в целях идентификации вмешивается в работу объекта, наносит специальные воздействия исследовательского характера. При этом управляющие связи, как правило, размыкаются, это может привести к нарушению нормального протекания технологического процесса, нарушению его режимов, что естественно может привести к значительным экономическим потерям. Поэтому такой эксперимент зачастую сложно реализовать в условиях действующей системы управления.

Активный эксперимент практически всегда связан с устранение прямых и обратных связей. Если управляющую связи не размыкать, то выходные воздействия объекта управления и соответствующие системы управления, также будет всегда приближаться к заданным значениям.

т.о. эффекты, нанесенные активным воздействием, активным характером будет компенсироваться уничтожаться, что не позволит построить адекватную математическую модель преобразования каналов объекта.

Мало того, что объект подвержен не контролированным возмущением (это практический характер для всех промышленных объектов), то активные воздействия необходимо наносить многократно, чтобы дальнейшим можно выявить более правильную реакцию объекта на эти воздействия.

Следует уделить особо на форму изменения активных исследований объектов на входе объекта. Нужно выполнять предпосылки.

Достоинство: если получение таких данных удовлетворяют предпосылки МНК и статистических методов идентификации, которые базируются на методе МНК. На основе этих данных могут быть получены адекватные модели.

Недостаток: сложность реализации из-за больших экономических потерь; возможность тяжелых последствий, например, авария на Чернобыльской АЭС.

2.3 Комбинированный эксперимент – такой, способ получения данные, который рациональным образом сочетается как активный, так и пассивный эксперимент. В настоящие время нет четких алгоритмов комбинирования видов экспериментов. На основе анализа опыта можно отметить следующие инженерные правила:

1) сочетание методов должно быть таким, чтобы обеспечить как получение эффективных данных для идентификации, так и уменьшение затрат и потерь в действующих системах при реализации такого эксперимента;

2) имеются основанные на опыте решения задач идентификации рекомендации: когда, при каких свойствах и условиях функционирования объекта и в какой последовательности проводить активные и пассивные эксперименты.

Такие рекомендации позволяют реализовать комбинированные эксперименты, которые в какой-то мере могут удовлетворять перечисленным выше требованиям.

Рекомендации:

1) начинать идентификацию надо с построения модели регулирующего канала;

2) если имеется несколько каналов регулирования, то идентификацию необходимо начинать с того, которым чаще пользуются в целях оперативного регулирования или который является более быстродействующим, т.е. имеет меньшее запаздывание и меньшую инерционность. Такой порядок проведения комбинированного эксперимента позволяет существенно сократить время функционирования объекта в разомкнутом режиме, т.е. без управления.

Рассмотрим пример, с помощью которого поясним один из вариантов комбинированного эксперимента. Пусть объект исследования является управляемым и имеет 2 входных воздействия, одно из которых является регулирующим u(t), а второе - контролируемым возмущающим воздействием w_k(t). Также на объект действуют неконтролируемые возмущения w_н(t) (рис.11).

Требуется: Оценить методами идентификации модели преобразующих каналов, т.е. найти математические модели φ_u{·}; φ_w{·}.

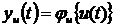; (47)

. (48)

При этом разрешено провести активный эксперимент, но с минимальным вмешательством в работу ОИ.

Рисунок 9 - Система регулирования объекта с двумя входными воздействиями.

Можно ли поставленную задачу решить при помощи данных пассивного эксперимента?

Первый вариант:

Можно, при выполнении следующих условий:

1) y*(t) = var

2) диапазон изменений контролируемых возмущений достаточно велик, чтобы оценить модель преобразующих каналов.

Чтобы выяснить, причем здесь условие 1, рассмотрим метод инструментальных переменных для оценивания параметра k уравнения вида y=kv + .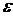

Сущность метода инструментальных переменных:

Пусть существует переменная z, удовлетворяющая следующим условиям:

1) 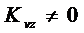; (49)

2) 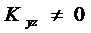; (50)

3) , (51)

где K_vz, K_yz, K_εz – корреляционные моменты (ковариации) между соответственно переменными v и z, y и z, ε и z.

То есть переменная z должна быть статистически связана с учитываемой переменной v, зависимой выходной переменной y и статистически не связана с эффектами неучитываемых факторов .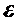

Чтобы показать основное уравнение метода инструментальных переменных для нахождения коэффициента 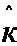, в исходном уравнении умножим левую и правую части на z:

yz = kvz+ 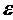z. (52)

Применим к обеим частям уравнения оператор математического ожидания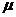

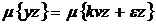(53)

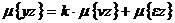(54)

Предположим, что 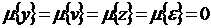, тогда оценка коэффициента k будет равна

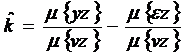(55)

С учетом свойств переменной z получим

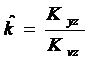(56)

Переменная z – инструментальная переменная. Её свойства сформулированы теоретически, исходя из условия эффективности метода наименьших квадратов. При этом, если учитываемые переменные v для управляемых объектов практически всегда связаны с эффектами прочих факторов ε, то авторы метода выдвигают гипотезу о существовании некоторой переменной z, названной инструментальной, которая должна удовлетворять записанным выше трем условиям. Потому что при выполнении именно этих условий задача идентификации по данным пассивного эксперимента для управляемых объектов может быть успешно решена.

Широкому практическому распространению метода инструментальных переменных препятствует лишь одно ограничение: где взять z?

В общем случае, справедливом для всех управляемых объектов, в качестве z может быть использовано задающее воздействие y*(t) в случае, если оно переменное.

Переменная y*(t) всегда статистически будет связана с y(t), поскольку y(t) для эффективного функционирования системы управления должна с заданной точностью отслеживать изменение y*(t). В свою очередь y*(t) будет связана и с u(t), так как эта связь обусловлена действующим в системе законом регулирования (к_yy≠0).

Эффективно функционирующая система управления должна отрабатывать задающее воздействие независимо от уровня, свойств и характера изменения неконтролируемых возмущений, следовательно, статистическая связь между y* и 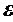практически всегда отсутствует.

Из анализа метода инструментальных переменных можно сделать вывод о том, что в случае, когда задающее воздействие – величина переменная, задачу идентификации регулирующего канала можно решить путем обработки данных пассивного эксперимента.

Для нашего примера модель 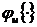может быть найдена методом инструментальных переменных на основе данных пассивного эксперимента. Поэтому будем считать, что половину 1- варианта задачи мы решили.

Для решения второй половины задачи выразим y(t) через её составляющие.

y(t) = y_u(t)+y_w(t)+y_wн(t); (57)

y_u(t) = 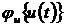; (58)

y_w(t) = 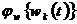; (59)

y_wн(t) – приведенные к выходу объекта возмущения.

1) предполагая, что y_wн(t) отсутствует или мало, можно записать:

y_w(t) = y(t) – y_u(t); (60)

y_u(t) можно рассчитать, зная модель регулирующего канала объекта и значения регулирующего воздействия u(t). Конечно, значения y_w(t) будет содержать дополнительные погрешности расчетов в отличие от тех значений y_w(t), которые можно было бы получить экспериментально.

Зная y_w(t) и w_k(t), можно решить задачу идентификации канала преобразования контролируемых возмущений, но при выполнении одного условия: если контролируемые возмущения w_k(t) будут изменяться в достаточно большом диапазоне.

Второй вариант:

Если же эти изменения невелики, то можно провести активный эксперимент, не разрывая управляющих связей. Например, нанести скачок по контролируемым возмущениям, при этом получим следующую картину (рисунок 10). Кривая I и II получаются в зависимости от настроек закона регулирования.

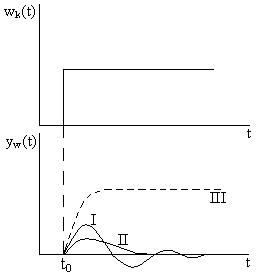
Рисунок 10 - Результат нанесения скачка по контролируемым возмущениям

Учтем, что эффективно работающая система регулирования должна удовлетворять двум основным требованиям:

ü быть устойчивой;

ü отвечать заданному критерию качества.

Поэтому отклонения y_w(t) от заданного уровня (кривые I и II на рисунке 10) должны быть малыми. Они в общем случае существенно не повлияют на эффективность работы системы регулирования (конечно, при разумной величине скачка w_k(t)).

В этом случае необходимо расчетным путем определить

y_w(t)= y(t)- y_u(t) (61)

по уже указанной схеме.

Кривая y_w(t), полученная расчетным путем, на графике обозначена кривой III при условии, что в качестве модели объекта по каналу преобразования контролируемого возмущения применяли модель инерционного звена 1-го порядка.

Сделаем следующие выводы по первой части примера:

Задачу идентификации управляемого объекта, имеющего 2 входных воздействия, одно из которых регулирующее, а другое – контролируемое возмущение, можно успешно решить поданным пассивного эксперимента.

Если выполняются следующие условия:

1. y*(t) – величина переменная, что позволяет ее взять в качестве инструментальной и использовать для идентификации регулирующего канала методом инструментальных переменных;

2. если диапазон изменения контролируемых возмущений w_k(t) достаточно большой, то можно решить задачу идентификации каналов преобразования контролируемых возмущений w_k(t) путем имитационного моделирования. Для реализации такого моделирования необходимо иметь математическую модель регулирующего канала объекта 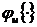и измеренные значения u(t), которые должны быть строго синхронизированы со значениями w_k(t). В процессе моделирования должны определяться

y_w(t)= y(t)- y_u(t) (62)

В такой моделирующей системе целесообразно использовать рекуррентные методы идентификации (см. лекции по идентификации).

Рекуррентные методы идентификации позволяют существенно уменьшить время моделирования, поскольку с их помощью оценка требуемых параметров модели последовательно уточняется на каждом шаге поступления данных.

3. Если диапазон измерения колебания возмущения W_k мал, то пассивного эксперимента не получится. Но в этом случае можно реализовать активный эксперимент по каналу контролируемых возмущений, через не разомкнутые рекуррентными связями. В этом случае система не теряет своей эффективности т.к. регулятор обратной связи скомпенсирует реакцию объекта на эти возмущения. Однако получиные данные изменяются y(t) позволят в этом случае получить адекватную модель φ_w{·}.

2) если y_wн(t) 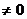, то используя описанную выше процедуру (формула 57), получим вместо y_w(t) оценку y_w(t) + y_wн(t). Если принять гипотезу о независимости этих двух составляющих или, что одно и то же, принять гипотезу о статистической независимости входных контролируемых и неконтролируемых переменных, эта задача может быть также решена.

Однако в этом случае, если иметь в виду последний вариант идентификации предыдущей схемы с нанесением скачкообразных изменений w_k(t), необходимо эксперимент продублировать несколько раз и полученные результаты усреднить по множеству.

При сглаживании по времени появляется дополнительное инерционное запаздывание, что при дальнейшей обработке полученных кривых приведет к смещенным оценкам.

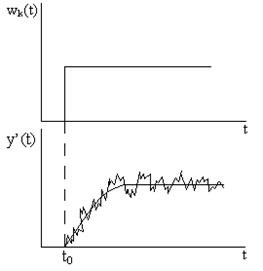
Рисунок 9 - Смещение оценок при инерционном запаздывании

y’_w(t) = y_w(t) + y_wн(t) (63)

Изменим второе условие. Пусть уровень контролируемых возмущений не велик, то есть для идентификации канала преобразования по контролируемым возмущениям необходимо наносить активные воздействия. Но при этом регулятор в обратной связи продолжает функционировать. В этом случае регулятор будет компенсировать эти активные исследовательские воздействия, но эффекты нанесенных регулирующих воздействий могут быть вычислены и исключены из y(t).

Расчет y_w(t) или y’_w(t) (формула 63) можно рассматривать как моделирование объекта при отключенной управляющей (регулирующей) обратной связи. При этом происходит расчетное размыкание цепей обратной связи или осуществляется перевод управляемого объекта в неуправляемый.

3) третий вариант: y*=const. В этом случае, для идентификации регулирующего канала требуется:

· размыкание обратной регулирующие связи;

· нанесение активных воздействий исследовательского характера по регулирующему каналу.

Этот вариант отличает от предыдущих двух тем, что здесь, для идентификации регулирования канала необходимо, править, активного эксперимента его в чистом виде, т.е. с размыканием регулирования, и нанесено активное возмущение исследовательского характера. Задача идентификации канала преобразуется в контролированное возмущение, полностью совпадает свыше рассмотренной ситуации.

Здесь целесообразно для уменьшения затрат времени использовать рекуррентные методы идентификации.

Рассмотренные способы получения данных: пассивный, активный и комбинированные эксперименты, можно получать как в ретроспективном варианте, так и в темпе с процессом.

В 1-ом случае необходимые экспериментальные данные получают любым способом, предварительно накопив необходимый или возможный объем выборки экспериментальных данных.

В этом случае обработка накопленных экспериментальных данных производится традиционными методами. Наиболее часто применяют для получения статических моделей - регрессионный и корреляционный анализ, а для динамических моделей корреляционный динамический анализ.

Кроме, такого способа данные могут быть получены и обработаны одновременно в темпе с поступлением данных с действующей системы управления. Для такой обработки применяют рекуррентные методы идентификации.

Рекуррентные методы идентификации используются еще и для нестационарных объектов, то есть таких, свойства которых с изменением времени или условий функционирования меняются, соответственно изменяются и параметры математических моделей или даже их структура.

Необходимым условием использования рекуррентных способов идентификации для нестационарных объектов является следующее:

v_д << v_z, (64)

где v_д – скорость дрейфа характеристик объекта;

v_z – скорость изменения учитываемых в модели переменных, т.е.

z={w,u,y}. (65)

Если это условие не выполняется (в частности, происходят резкие и существенные изменения характеристик объекта), то рекуррентные процедуры не гарантируют эффективное отслеживание параметров модели объекта.

Date: 2015-07-22; view: 565; Нарушение авторских прав