А по МНК должно быть

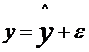
U(t)=∫E(t)dt

Рассмотрим уравнение:

Y=ku+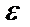

Умножим на U:

Y*u = k*u2+ 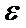*u

Тогда, математическое ожидание:

M{yu}=M{ k*u2+ 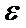*u }

M{y}=M{u}=0

Kyu=1/N*∑(ui-uср)

K=Kyu/Дu

1) Исходные данные не должны содержать выбросов или грубых ошибок.

2) Структура математической модели должна быть линейно-параметрической, т.е. линейной по отношению к параметрам, и таких структур может быть много.

Если структура зависимости известна и не линейна, то ее можно привести к линейно-параметрическому виду, в частности, используя точное математическое преобразование, либо приближенное, например, путем разложения в ряд (любой ряд, имеющий линейно-параметрическую структуру).

3) Критерий точности должен быть среднеквадратический, т.е. он дифференцируемый, непрерывный (например, среднемодульный прерывается в 0).

МНК получен в результате решения задачи оптимизации аналитическим путем. Точное решение задачи оптимизации возможно лишь в случае ЛКГ, где Л - линейность модели к искомым переменным, К – квадратичность критерия, Г – «гауссовость» эффектов неучитываемых факторов (ε), т.е. с нормальным законом распределения.

4) Выходная переменная у распределена нормально для каждого фиксированного значения входной величины v_j, 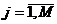, M – число факторов, учитываемых моделью, т.е. ε распределено нормально. Предпосылка не говорит о том, что выходная переменная Y должна быть распределена нормально, а нормальным распределение должно быть для эффектов не учитываемых факторов ε. Проверить можно в том случае, если реализовать так называемые дублирующие опыты, т.е. для одних и тех же постоянных значений V провести серию экспериментов. Значения выходной переменной в этой серии будут отличаться друг от друга за счет влияния неизвестных факторов (Wн). Эти отклонения можно определить, как разность экспериментальных значений y и выборочной средней, значения которой находятся по результатам усреднения значения y в дублирующих экспериментах.

5) Постоянно действующее возмущение ε представляет собой последовательность независимых случайных величин с нулевым средним значением и некоторой неизвестной дисперсией (постоянной), т.к. задача решается ЛГК

Если зафиксировать последовательно входную переменную и проводить эксперименты, то т.к. 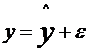, то ε будет статистически независимой. Если на интервале объекта имеется связь между переменными (т.е. объект динамический), то следующий эксперимент проводить через t больше интервала памяти объекта. Если ограничение не будет исполняться, то будет смещение в зависимости от коэффициента корреляции.

6) Дисперсия должна быть однородной, т.е. при увеличении числа выборки оценка будет не смещенной, и приближаться к полученной по генеральной совокупности.

Генеральная совокупность – это такая совокупность, объем которой равен ∞.

Поскольку практически генеральную совокупность в процессе эксперимента получить невозможно, то экспериментатор всегда получает часть этой совокупности, которая называется выборочной, т.е. однородная дисперсия – это такая дисперсия оценки, которой принадлежат одной и той же генеральной совокупности.

Для проверки гипотезы принадлежности двух полученных экспериментальным путем дисперсий одной и той же совокупности американский ученый Фишер предложил процедуру, основанную на следующем критерии:

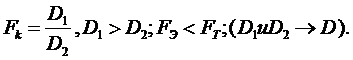
Критерий Фишера. Есть 2 оценки дисперсии: D₁ и D₂. Принадлежат ли они одной генеральной совокупности?

, при D₁ > D₂. Если полученная величина меньше табличной, то они принадлежат одной генеральной совокупности. Дисперсия ε должна быть постоянная (однородная) при зафиксированных v_j.

7) Отсутствие статистической связи между эффектами неучтенных факторов ε и учтенными факторами v_j.

8) Последовательность значений v_j, реализованных в процессе эксперимента, должны быть независимы между собой, т.е. v_j(i) должны быть статически независимо от v_j(i+ 1 ), где j - номер фактора, 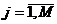, i -номер эксперимента. Аналогичное требование накладывается и на y (как следствие). Поскольку МНК использует для нахождения статических зависимостей, а практически все реальные объекты являются динамическими, то для выполнения этой предпосылки необходимо интервал времени между двумя соседними экспериментами брать больше, чем время памяти объекта, т.е. после того, когда все переходные процессы в объекте, обусловленые предыдущим экспериментом, закончатся.

9) Учитываемые факторы v_j и v_к при к≠j между собой статистически независимы. Нарушение этой предпосылки приводит к смещению оценок параметров при этих факторах. Они не будут отражать реально существующее соответствие между y и v_j. Если эти факторы очень тесно связаны (r≈ 0,9 ), то один из факторов нужно исключить (который легче реализовать). Если коэффициенты корреляции между этими факторами небольшой, например r меньше либо равно 0.5, то их исключать нельзя: надо проводить ортогонализацию факторов.

10) Входная величина v_j не должна содержать ошибок измерения. т.е. учитываемые факторы v_j является неслучайными и управляемыми факторами. Погрешность всегда будет, но она должна будет существенно малой, по сравнению с диапазоном изменения измеряемой величины. Исследователь может изменять значения входных переменных в соответствии с предварительно разработанным планом.

Вывод: предпосылки в основном выполняются при активном эксперименте. Нарушение предпосылок всегда будет приводить к смещению полученных оценок, но в различной степени. Главное – это независимость факторов v_j и ε и отсутствие статистической связи между v_j и ε (если используется пассивный эксперимент).

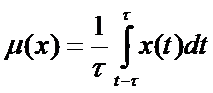
Д – мера разброса значений вокруг какого-то среднего:

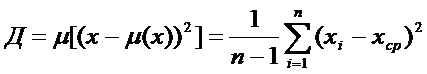
Date: 2015-07-22; view: 406; Нарушение авторских прав