Основное уравнение идентификации и методы его решения

Однойиз наиболее распространенных форм математического описа­ния линейных динамических объектов в непараметрической форме является весовая, или импульсная переходная функция g(t). Эта характеристика однозначно описывает динамические свойства объекта.

Рассмотрим линейную динамическую систему с одним входом и выходом. Выход объекта y(t) связан со входом x(t) некоторым оператором А.

Представим x(t) в виде разложения по системе -функций;

X(t)= 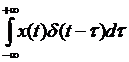(82)

Здесь (t - 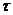) - -функция, действующая в момент времени, равный 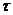. Поскольку рассматриваемая система линейна, для нее справедлив прин­цип суперпозиции:

A 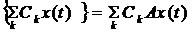(83)

Поскольку y(t)=Ax(t), то

y(t)=A 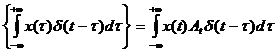(84)

Здесь 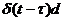= g(t, 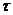) – реакция объекта на -функцию, т.е. импульсная переходная функция.

Если сигнал на входе системы появляется, начиная с момента t=0, выражение (71) примет вид

Y(t) = (85)

Дли стационарных объектов интеграл-свертки записывается следующим образом:

Y(t)= 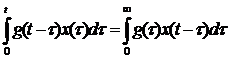(86)

Установим связь между статистическими характеристиками объекта управления. Известно, что взаимная корреляционная функция стационарного случайного процесса определяется по формуле

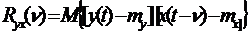(87)

Подставим в (74) значение y(t) из (73):

R _xy(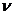)= 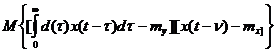(88)

Учитывая, что 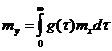,получим:

R _yx(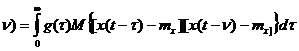 (89)

Т.к. 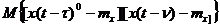есть автокорреляционная функция входного сигнала R 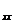(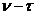) 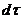, то в итоге запишем следующее уравнение:

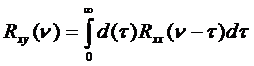(90)

Это уравнение называют основным уравнением идентификации [5] или уравнением Винера-Хопфа. При выводе уравнения (77) рассматривались центрированные входные и выходные сигналы, мат.ожидание которых равно нулю. Однако уравнение (77) справедливо и для нецентрированных сигналов x(t) и y(t), т.е. содержащих неслучайную составляющую.

Пусть входной сигнал x(t) представляет собой белый шум. Автокорреляционная функция белого шума является функцией. 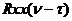= 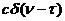, где с –известная постоянная величина, характеризующая спектральную плотность белого шума. Тогда в соответствии со свойствами - функции получим:

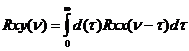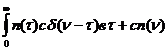= ; (91)

. (92)

Таким образом, взаимная корреляционная функция выходного и входного сигналов объекта в случае, когда входной сигнал является белым шумом, пропорциональна импульсной функции переходной функции объекта.

Рассмотрим влияние помех при измерении сигналов x(t) и y(t) на определение импульсной переходной функции. Вначале будем считать, что с помехой измеряется только входной сигнал

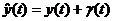. (93)

Тогда

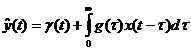. (94)

Умножив (81) на x(t- 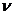) и усреднив результат на интервале Т, Т 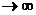, получим:

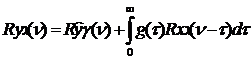. (95)

Наличие помехи привело к тому, что в уравнении Винера-Хопфа появилось дополнительное слагаемое 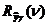- взаимокорреляционная функция сигнала 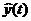и помехи .

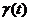Для того, чтобы помеха 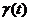не сказалась на результате идентификации, требуется, чтобы =0, т.е. помеха и выходной сигнал были некоррелированны.

Пусть сигнал y(t) измеряется без помех, а входной сигнал измеряется с помехой 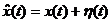. При этом имеет место соотношение

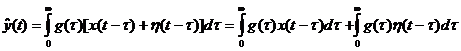(96)

Умножив (83) на [ 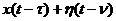] и усреднив результат по времени, получим:

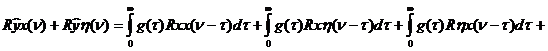
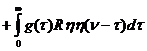(97)

Для большинства реальных объектов можно считать, что помехи измерения являются некоррелированными с результатом измерения и кроме того, значения входного сигнала некоррелированны с помехами при измерении x(t). Тогда 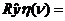0; 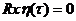; 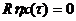и уравнение (83) примет вид

; (98)

Из этого уравнения видно, что помеха на входе приводит к ошибкам в определении весовой функции. Этот же вывод можно распространить на случай, когда с помехой измеряется и входной, и выходной сигналы.

Уравнение Винера-Хопфа относится к классу интегральных уравнений Фретгольма I рода. В общем случае такое уравнение записывается в виде

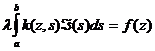, (99)

где 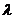- параметр; в уравнении идентификации 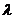= I;

k(z,s) -ядро уравнения; в уравнении идентификации ядром уравнения является корреляционная функция;

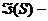искомая функция (импульсная весовая функция);

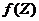- свободный член (взаимнокорреляционная функция R _yx()).

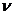Для решения уравнения идентификации могут быть применены методы, разработанные в теории интегральных уравнений и в вычислительной математике для решения интегральных уравнений Фретгольма I рода [4.13].

Одним из наиболее простых методов решения (90) является конечно-разностный метод. Заменим бесконечный верхний предел у интеграла и уравнении Винера-Хопфа конечной величиной Т:

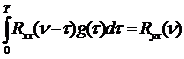(100)

Применим один из методов численного интегрирования – метод прямоугольников. Тогда (87) запишется в виде

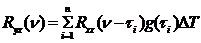, (101)

где ;

Учитывая, что 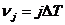, , 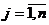представим уравнение (88) в векторно-матричной форме:

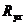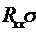= . (102)

Здесь

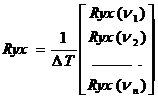; (103)

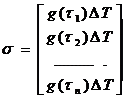; (104)

(105)

Рассмотрим как образуются элементы матрицы R_xx:

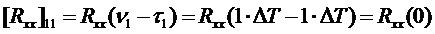, (106)

т.е. дисперсия выходного сигнала

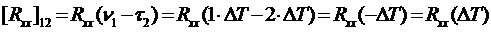, (107)

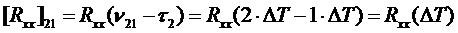и т.п. (108)

Из уравнения (89) находим:

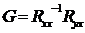(109)

При решении этого уравнения на ЭЦВМ для обращения матрицы пользуются стандартными подпрограммами (СП). В библиотеках СП часто имеются несколько подпрограмм обращения матриц, работающих по разным алгоритмам. Алгоритмы вычисления обратных матриц описаны в литературе по численным методам.

Рассмотрим аналог уравнения Винера-Хопфа для дискретного случая. Допустим, что измерения сигналов на входе и выходе линейного динамического объекта производятся с постоянным шагом квантования 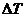Тогда уравнение (96) можно записать в виде

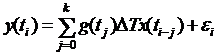, (110)

где 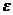_i-невязка (иногда называемая шумом).

Невязка состоит из реакций на другие входы системы и ошибок в линейной модели, возникающих из-за предположения, что объект линейный и стационарный, а так же из-за замены интегрального уравнения дискретной суммой.

Пусть i=k,k+1,….,N, причем N-k >k. Запишем уравнение (110) в развернутом виде:

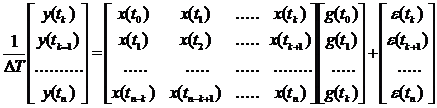(111)

или в символическом виде:

Y=XG+E. (112)

Оценим вектор G из условия

. (113)

Необходимым условием минимума 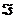является

(114)

Из этого условия получаем уравнение Винера-Хопфа в дискретной форме:

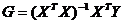(115)

Матрица Х^тХ представляет собой квадратную матрицу размером (х+1)*(к+1). Элементы ее определяются следующим образом:

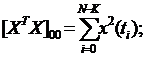(116)

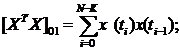(117)

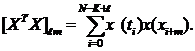(118)

Date: 2015-07-22; view: 536; Нарушение авторских прав