Виды моделей

Рассмотрим классификацию моделей по нескольким признакам:

1. По признаку, связанному с физической природой модели.

1.1 Натурная модель

Натурная модель – комплексы (природные, технические), особенности поведения которых во времени достаточно изучены для того, чтобы можно было установить их аналогию (подобие) с другими комплексами [3].

Натурная модель - реально изучаемые объекты или их части [4].

Примером натурных моделей могут быть действующие агрегаты, процессы, протекающие в них, которые исследуются (проводятся эксперименты), чтобы проектировать аналогичный агрегат или процесс. При этом предполагается, что проектируемый объект будет функционировать в таких же или аналогичных условиях, тогда результаты, полученные на натурной модели, можно переносить на проектируемые объекты. Такие модели часто называют аналогами проектируемого объекта.

Если условия оригинала несколько отличаются от условий натурной модели, то результаты, полученные в натурной модели, следует обязательно корректировать.

1.2 Физическая модель

Физическая модель – установка, устройство или приспособление, позволяющее исследовать систему путем замещения изучаемого физического процесса подобным ему процессом той же или другой физической природы [4].

Физическая модель – модель, воспроизводящая главные процессы изучаемого явления с сохранением его природы и основных влияющих факторов [3].

Примером физической модели является уменьшенная или увеличенная геометрически подобная копия оригинала (макет квартала жилого массива, планетарная модель атома). Эти модели могут быть как статическими, так и динамическими. В последнем случае в них можно реализовать физические явления или процессы подобные процессам оригинала. При этом процессы могут иметь одну и ту же физическую природу (макет русла реки и ГЭС), но могут иметь и другую физическую природу (физическая модель МНЛЗ). Как правило, подобие между физическими процессами устанавливается методами теории подобия, с помощью специальных критериев подобия.

Сравнивая приведенные два определения физической модели, отметим, что первое определение источника [4] является более правильным, потому что физическая модель может быть построена на основе другой физической природы, чем у оригинала. При этом выбор другой более простой физической природы модели основывается на положениях специально разработанной для этого теории подобия.

Далее рассмотрим понятие математической и комбинированной модели. В качестве представителя комбинированной модели будем рассматривать натурно-математические модели. Дальнейшее изложение лекционного материала будет связано именно с математическими и натурно-математическими моделями.

1.3 Математическая модель

Математическая модель – система математических соответствий, описывающих изучаемый процесс или явление [2].

Математическая модель – формальная система, представляющая собой конечное собрание символов и совершенно точных правил оперирования этими символами в совокупности с интерпретацией свойств определенного объекта с некоторыми символами, отношениями и константами [5].

Математические модели в настоящее время наиболее широко используются для описания натурных объектов различной природы. Однако математические модели имеют свою ограниченную область применения, в частности, в настоящее время практически невозможно описать с помощью этих моделей поведение человека как элемента системы управления.

Для многих сложных систем управления можно построить математическую модель, но зачастую она имеет сложную структуру и соответственно большое число неизвестных параметров (коэффициентов), значение которых необходимо определить. Это требует больших затрат средств и времени. Именно по этим двум причинам в последнее время все чаще используют комбинированные модели, которые оказываются более адекватными для таких объектов.

Математическая модель, также, как и другие виды моделей, называется адекватной, если она с заданной точностью отражает необходимые свойства и условия функционирования натурного объекта.

При этом понятие точности связано с ошибкой.

ε = y^н - y^м , (1)

где у ^Н – натурное значение выходной переменной объекта;

у ^М – модельное значение выходной переменной объекта, полученное с помощью математической модели.

Соответственно, для оценивания точности модели используют критерии точности. Чаще всего это критерии следующего вида:

- среднеквадратический

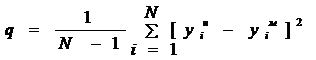- в дискретном времени (дисперсия); (2)

- в непрерывном времени; (3)

где T, N – интервал времени или число данных, на котором осуществляется моделирование.

- среднемодульный критерий имеет разрыв в нуле.

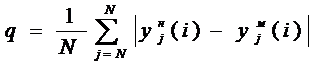- в дискретном времени; (4)

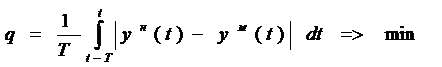- в непрерывном времени. (5)

Среднеквадратический критерий используется чаще в теоретических расчетах. Он удобен при аналитическом решении задач, но им можно пользоваться, если натурные данные не содержат грубых ошибок, а если такие данные содержат грубые ошибки, то используется среднемодульный критерий.

Любое ли математическое выражение можно считать математической моделью?

Ответ в источнике [3]. Любое математическое выражение можно считать математической моделью, если оно удовлетворяет 3 условиям:

ü за этим выражением всегда стоит натурный объект, процесс, явление (оригинал). Это условие следует понимать так, что все переменные математического выражения должны быть проинтерпретированы в терминах оригинала.

ü между этим аналитическим выражением и оригиналом должно быть установлено соответствие. То есть модель, являясь заменителем оригинала, должна поставлять исследователю, данные с требуемой точностью, то есть отклонение между натурными и расчетными данными должно быть по модулю меньше заданного малого числа.

ü с моделью можно оперировать существенно легче и проще, чем с оригиналом.

1.4 Комбинированные модели

Комбинированные модели – такие модели, которые представляют собой комбинацию натурной и математической или физической моделей.

Остановимся на натурно-математических моделях, которые относятся к типу комбинированных и представляют собой некоторую комбинацию математических моделей и натурных частей системы оригинал. Необходимость в такой модели вызвана тем, что во многих практических задачах чисто математические модели либо не в состоянии отобразить требуемые свойства и условия функционирования оригинала с заданной точностью, либо это очень сложно и связано с большими затратами средств и времени.

В данном случае под натурным объектом понимаем данные, информационное отображение (любой натурный объект является частью СУ).

Возникает вопрос, каким образом реализовывать комбинацию натурных частей системы с математическими выражениями и моделями. Следует сразу же оговориться, что такое соединение осуществляется не непосредственно с натурным объектом, а с его информационным отображением.

Информационное отображение натурного объекта или системы – это упорядоченная и синхронизированная совокупность реализаций исходных данных, полученных из действующей системы контроля и характеризующих изменение во времени всех входных и выходных воздействий и переменных состояния натурного объекта.

Это информационное отображение может быть использовано в задачах моделирования либо в темпе с процессом, когда моделирующая система непосредственно встроена в систему управления или тесно с ней связана. В этом случае исходные данные поступают в моделирующую систему с тем интервалом (темпом, шагом), который реализован в действующей системе контроля. Либо можно использовать ретроспективный вариант, когда это информационное отображение предварительно записано на специальные носители данных, а затем воспроизводится в требуемом масштабе времени.

Первый вариант особенно важен, когда действующая АСУ реализует не только функции рабочего управления системы, связанные с измерением, контролем, регулированием, оптимизацией, но и обеспечивающие функции, реализуемые в таких подсистемах, как исследовательская система, испытательно – наладочная и обучающая, в которых параллельно с рабочими системами решают задачи идентификации, оптимизации, настройки системы управления, обучения персонала.

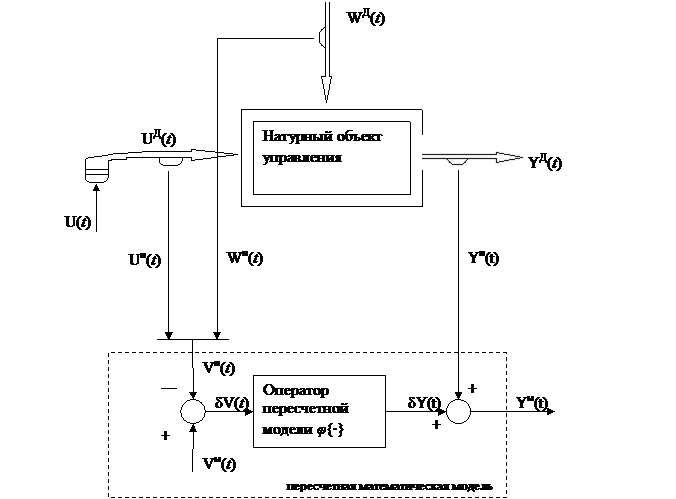
Рисунок 1 - Структура пересчетной модели

При таком моделировании возникает задача сочленения натурных данных с модельными. Ее осуществляют с помощью математических моделей специального класса, называемых пересчетными математическими моделями (рис 1.). Эти модели «работают» в приращениях к натурным данным и позволяют ответить на вопрос, что было бы на выходе объекта исследования, если вместо натурных входных воздействий действовали бы другие модельные значения входных воздействий. Натурно – математическую модель управления объекта с использованием пересчетной модели в общем виде можно записать следующим образом.

Y ^М(t) = Y ^Н(t) + δY (t) (6)

dY (t) = 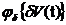(7)

δV (t) = V ^М(t) – V ^Н(t) (8)

Пересчетная модель рассчитывает абсолютные значения. Оператор пересчетной модели не рассчитывает абсолютные значения выходной переменной, а пересчитывает отклонения выходных воздействий в зависимости от отклонений входных воздействий. Оператор пересчетной модели φ_υ{·} имеет то преимущество по сравнению с математической моделью, что структурно он является более простым. Это объясняет тем, что с его помощью преобразуются отклонения входных воздействий относительно их натурных значений, т.е. диапазоном изменения δV существенно меньше.

В самом общем виде математические модели можно представить с помощью следующих выражений:

Y = Ф ₁ { W, U, A, t }; (9)

Y = Ф ₂ { V, A, t }; (10)

Во втором выражении вместо W и U стоит символ V – вектор входных воздействий без разделений его на управляющие и внешние. По этому отличию можно сразу же отметить, что первое выражение представляет собой математическую модель преобразующих каналов объектов управления, т.к. здесь в явном виде выделены управляющие и внешние воздействия.

Вторым выражением представлена математическая модель объекта исследования, который не является объектом управления, т.е. не является частью системы управления, т.к. в нем отсутствует разделение входных воздействий на внешнее и управляющее.

В зависимости от подхода к построению моделей выделяют два класса математических моделей:

1) математические модели внутреннего механизма процесса или математические модели «в большом»;

2) функциональные или кибернетические модели или модели «в малом».

Будем в дальнейшем обозначать через Ф { ∙ } модели внутреннего механизма процесса, а через φ { ∙ } – функциональные (кибернетические) модели.

Выражения (9) и (10) записаны с помощью заглавных символов, то есть речь идет о математической модели поведения объекта во всем большом диапазоне изменения входных и выходных воздействий. Такие модели называют математическими моделями «в большом» или математическими моделями внутреннего механизма процессов, происходящих в объекте. Как правило, такие модели детально отображают все требуемые стадии преобразования энергии или вещества в объекте.

Функциональные модели представлены с помощью выражений (11)-(14):

y = φ₁ {w, u, a, t} (11)

y = φ₂ {v, a, t} (12)

y = φ₃ {w, u, a} (13)

y = φ₄ {v, a} (14)

11, 12 – динамические; 13,14 – статические.

Модели типа (11)-(14) называются кибернетическими или функциональными. Они отражают поведение объекта в малом диапазоне изменения входных и выходных воздействий. Эти модели отражают лишь внешнее соответствие, причинно-следственную связь между входными и выходными воздействиями и совершенно не затрагивают процессы преобразования энергии или вещества внутри объекта.

По временному признаку классификации выделяют статические и динамические модели.

Динамические модели в явном виде отражают динамику изменения состояния объекта. Примером таких математических моделей, записанных в общем виде, является выражение (9)-(10) и (11)-(12), т.к. в этих моделях в качестве аргумента указано непрерывное время t.

Модели, которые не учитывают изменение объекта во времени, называются статическими. В общем виде они представлены выражениями (15)-(16) и (13)-(14). Статические модели, так же как и динамические, могут быть представлены как моделями «в большом», так и моделями «в малом».

Y = Ф₃ {W, U, A} (15)

Y = Ф₄ {V, A} (16)

Модели (15) и (16) отражают поведение объекта в статическом состоянии в установившиеся моменты времени, без учета времени. Они называются статическими и совершенно не отражают переходы объекта из одного состояния в другое.

Модели (9) и (10) – динамические модели, отражающие поведение объекта с учетом времени, то есть отражают его динамику.

Применительно к объекту управления модели (9) и (10) являются моделями преобразующих каналов объекта.

Примером статической модели, наиболее часто используемой на практике, является полиномиальная модель. Она имеет такую структуру:

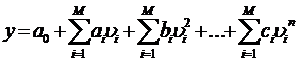(16a)

где 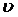- входное воздействие (переменная);

M – число учитываемых моделью входных воздействий.

n – степень полинома.

Ввели новое понятие: «структура модели». В дальнейшем под этим будем понимать различную форму связи между зависимой переменной (функцией) и независимой переменной (аргументом).

Эта структура модели (16a) используется очень часто при построении функциональных моделей. Она является линейно-параметрической. Структура модели является линейно-параметрической, если она линейна по отношению к коэффициентам (параметрам) a_i, b_i, … c_i, но может быть нелинейна по отношению к аргументам .

Примером динамической модели являются дифференциальные уравнения, как обычные, так и в частных производных. При этом обычные дифференциальные уравнения используются для отображения свойств натурных объектов с сосредоточенными переменными, а уравнения в частных производных - для отображения свойств объектов с распределенными переменными.

Под объектами с сосредоточенными переменными будем понимать такие объекты, состояние которых характеризуется набором физических величин, имеющих одинаковые значения в одно и то же время, но в различных точках пространства.

Под объектами с распределенными переменными будем понимать объекты, состояние которых характеризуется набором физических величин, имеющих различные значения в одно и то же время, но в различных точках пространства.

Если речь идет о динамических моделях, то будем различать 2 класса таких моделей:

- в непрерывном времени (t);

- в дискретном времени (i).

В последнем случае дискретное время (i) представлено номером отсчета. Это справедливо при одинаковом шаге (интервале) дискретизации.

Если записать в непрерывном времени дифференциальное уравнение, например, линейное дифференциальное уравнение 1-го порядка с запаздывающим аргументом.

,

то это уравнение в дискретном времени имеет вид:

y(i) = c₁ y (i - 1) + c₂ v (i - l) - это рекуррентное дифференциально-разностное уравнение.

где l – дискретное запаздывание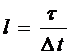

Переход от непрерывного дифференциального уравнения к дифференциально-разностному осуществляется за счет замены производной ее приближенным уравнением. Таких приближений может быть несколько. Наиболее простые из них:

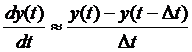- левая разность

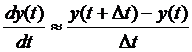- правая разность

Date: 2015-07-22; view: 2706; Нарушение авторских прав