Критерии выбора стратегии

Проведем анализ стратегий производства при неопределенной рыночной конъюнктуре. Для выбора наилучшей стратегии поведения на рынке товаров и услуг существуют различные критерии, среди которых можно назвать критерии: Байеса, Лапласа, Вальда, Сэвиджа, Гурвица и максимакса. Нет никаких оснований считать априори один из критериев лучше, чем другие, однако вернее будет выбрать ту стратегию, которая будет предпочтительнее по нескольким критериям.

Критерий Байеса используется, если в результате исследований известны вероятности всех состояний «природы» (q_j). При этом, если учтены все из n возможных состояний, то

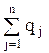= 1.

В этом случае в качестве показателя, который необходимо максимизировать, берется среднее значение выигрыша

B = 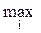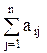× q_j.

Определим наилучшую стратегию по критерию Байеса:

30 × 0,2 + 22 × 0,4 + 16 × 0,3 + 8 × 0,1 = 20,4,

6 × 0,2 + 40 × 0,4 + 32 × 0,3 + 24 × 0,1 = 29,2,

-18 × 0,2 + 16 × 0,4 + 50 × 0,3 + 42 × 0,1 = 22,0,

-42 × 0,2 - 8 × 0,4 + 36 × 0,3 + 60 × 0,1 = 4,8.

Наилучшая стратегия С₂ дает максимальный средний «выигрыш» в размере 29,2 ден.ед.

Критерий Лапласа применяется в случае наибольшей неопределенности обстановки. При этом все n состояний «природы» принимаются равновероятными, т.е. вероятность каждого из состояний q_j = 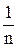. Согласно этому критерию «недостаточного основания» находится максимальный «средний» выигрыш.

L = .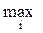

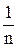
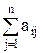Определим наилучшую стратегию по критерию Лапласа:

(30 + 22 + 16 + 8)/4 = 19,0,

(6 + 40 + 32 + 24)/4 = 25,5,

(-18 + 16 + 50 + 42)/4 = 22,5,

(-42 - 8 + 36 + 60)/4 = 11,5.

Наилучшая стратегия С₂ дает максимальный средний «выигрыш» в размере 25,5 ден.ед.

Критерий Вальда – это максиминный критерий крайнего пессимизма, или наибольшей осторожности, перестраховки. Такой подход характерен для того, кто очень боится проиграть и считает природу разумным, вредным и агрессивным конкурентом, назло мешающим нам достигнуть успеха. В этом случае оптимальной стратегией для игрока С_i будет чистая стратегия С, при которой наименьший «выигрыш» будет максимальным, т.е. при которой гарантируется выигрыш, в любом случае не меньший, чем нижняя цена игры с природой:

V = 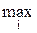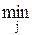а_ij.

Используя матрицу игры, определяем минимальный выигрыш для всех стратегий

a₁ = 8; a₂ = 6; a₃ = -18; a₄ = -42.

Наилучшая стратегия С₁ дает максимальный (из минимальных) «выигрыш» в размере 8 ден.ед.

Критерий Сэвиджа сводится к тому, чтобы любыми путями избежать большого риска при принятии решения. Оптимальной будет стратегия С_i, при которой минимизируется величина максимального риска в наихудших условиях:

S = 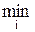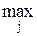r_ij.

Используя матрицу рисков, находим максимальные риски для всех стратегий

r₁ = 52 r₂ = 36 r₃ = 48; r₄ = 72.

Наилучшая стратегия С₂ допускает минимальный риск (из максимальных) в размере 36 ден.ед.

Критерий крайнего оптимизма (максимакса) предполагает выбор стратегии, при которой из самых больших «выигрышей» для каждой стратегии выбирается наибольший. Этот критерий характерен для легкомысленного руководителя, полагающегося на «авось»:

M = 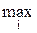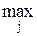а_ij.

Наивыгоднейшая стратегия может дать «выигрыш» в размере 60 ден.ед., но ей же соответствует и наибольший риск (72 ден.ед.).

Критерий Гурвица является линейной комбинацией пессимистической и оптимистической позиций. Стратегия выбирается из условия

G = 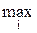{k × 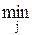а_ij + (1 - k) × 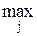а_ij},

где k – коэффициент «пессимизма».

Коэффициент k меняется от 0 до 1, не принимая этих граничных значений (0 < k < 1). Коэффициент k выбирается на основании опыта или из субъективных соображений. Чем опаснее ситуация, тем менее мы склонны к риску, тем больше мы хотим подстраховаться, а значит, тем ближе к единице выбирается k. При k = 1 критерий Гурвица превращается в критерий Вальда, а при k = 0 – в критерий «крайнего оптимизма». Примем k = 0,6, тогда

0,6 × 8 + 0,4 × 30 = 16,8,

0,6 × 6 + 0,4 × 40 = 19,6,

0,6 × (-18) + 0,4 × 50 = 9,2,

0,6 × (-42) + 0,4 × 60 = -1,2.

Наилучшая стратегия С₂ дает «выигрыш» в размере 19,6 ден.ед. По большинству критериев наилучшей стратегией является С₂, т.е. объем производства равен 400 изделиям.

Date: 2015-07-24; view: 621; Нарушение авторских прав