
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Игры 2 х n и m х 2
|
|
Допустим, платежная матрица задана и имеет вид 2 х n:
| В1 | В2 | … | Вn | Игрок А имеет две стратегии, а игрок В – неограниченное число стратегий. | |
| А1 | a11 | a12 | … | a1n | |
| А2 | a21 | a22 | … | a2n |
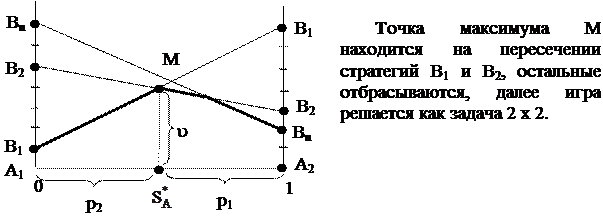 |
Допустим, платежная матрица имеет вид m х 2:
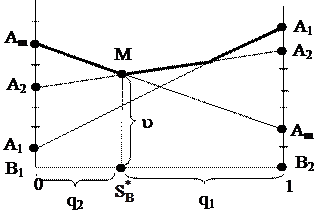 |
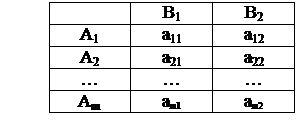 |
Минимум М находится на пересечении стратегий А1 и Аm, остальные отбрасываются, далее игра решается как задача 2 х 2.
Пример. Пусть игра задана в виде платежной матрицы
| В1 | В2 | В3 | Игра (2 х 3) не имеет седловой точки a = 4, b = 5, a ¹ b, имеем игру в смешанных стратегиях. | |
| А1 | ||||
| А2 |
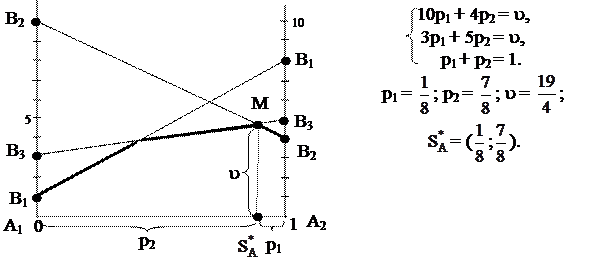 |
Решим задачу графически и аналитически. Для игрока А: получаем игру 2 х 2, используя стратегии В2 и В3 игрока В:
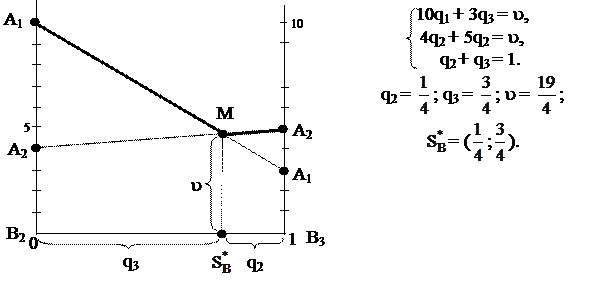 |
Для игрока В:
Тема 8. Элементы теории статистических игр. Игры с «природой»
В рассмотренных случаях оба игрока действовали наилучшим для себя способом. Однако встречаются конфликтные ситуации, в которых одна из сторон действует неопределенно, она безразлична к выигрышу и не стремится воспользоваться промахами другой стороны. Такая игра возникает, когда у нас нет достаточной осведомленности об условиях данной операции (например, условия погоды, покупательский спрос на продукцию и т.д.). Игры такого типа, когда человек вынужден выбирать стратегию (принять решение) в условиях неопределенности, называют играми с «природой», состояние которой ему полностью не известно.
Под термином «природа» будем понимать комплекс внешних обстоятельств, при которых приходится принимать решения. Игры с «природой», т.е. когда одним из участников является человек (игрок С), а другим - «природа» (игрок П), называют также статистическими играми.
В общем виде постановка задачи теории статистических игр производится следующим образом. Пусть имеется m возможных стратегий (линий поведения) - С1, С2, …, Сi,…, Сm; условия обстановки – состояние «природы» нам точно не известно, однако о них можно сделать n предположений П1, П2, …, Пj,…Пn, которые являются как бы стратегиями «природы», результат игры – «выигрыш» аij - при каждом сочетании стратегий задан матрицей игры
| П1 | П2 | … | Пj | … | Пn | |
| С1 | а11 | а12 | … | а 1j | … | а 1n |
| С2 | а21 | а 22 | … | а 2j | … | а 2n |
| … | … | … | … | … | … | … |
| Сi | аi1 | а i2… | … | а ij | … | а in |
| … | … | … | … | … | … | … |
| Сm | аm1 | а m2 | … | а mj | … | а mn |
Необходимо выбрать наилучшую стратегию поведения, которая по сравнению с другими наиболее выгодна.
Допустим, фирма должна определить уровень выпуска продукции и предоставления услуг на некоторый период времени, так, чтобы удовлетворить потребности клиентов. Точная величина спроса на продукцию и услуги неизвестна, но ожидается, что в зависимости от соотношения сил на рынке товаров, действий конкурентов и погодных условий спрос может принять одно из четырех возможных значений: 300, 400, 500 или 600 изделий. Маркетинговые исследования позволили определить возможные вероятности возникновения этих ситуаций, которые соответственно составили 0,2; 0,4; 0,3 и 0,1. Для каждого из возможных значений спроса существует наилучший уровень предложения с точки зрения возможных затрат и прибыли. Отклонение от этих уровней связано с риском и может привести к дополнительным затратам либо из-за превышения предложения над спросом, либо из-за неполного удовлетворения спроса. В первом случае это связано с необходимостью хранения нереализованной продукции и потерями при реализации ее по сниженным ценам, а также с транспортными расходами по доставке ее в другие регионы, где она будет пользоваться спросом. Во втором случае это связано с дополнительными затратами по оперативному выпуску недостающей продукции, поскольку иначе это будет связано с риском потери клиентов. Данную ситуацию можно представить в виде матрицы игры
| Объем предложения (стратегия выпуска продукции) | Возможные колебания спроса на продукцию | |||
| П1 = 300 | П2 = 400 | П3 = 500 | П4 = 600 | |
| Вероятности состояния спроса | ||||
| q1 = 0,2 | q2 = 0,4 | q3 = 0,3 | q4 = 0,1 | |
| Размер прибыли (убытков) в зависимости от колебаний спроса аij | ||||
| С1 = 300 | ||||
| С2 = 400 | ||||
| С3 = 500 | -18 | |||
| С4 = 600 | -42 | -8 |
Из этой таблицы видно, что при обстановке П1 решение С1 в 5 раз лучше, чем С2. Необходимо выбрать наиболее выгодную стратегию. Наибольший выигрыш в 60 ден.ед. дает стратегия С4 при возникновении обстановки П4.
В теории статистических игр вводится специальный показатель, который называется риском. Риск показывает, насколько выгодна применяемая стратегия в данной конкретной обстановке с учетом ее неопределенности. Риск рассчитывается как разность между ожидаемым результатом действий при наличии точных данных об обстановке и результатом, который может быть достигнут, если эти данные точно не известны. Например, если точно известно, что будет иметь место обстановка П4, то лучшее решение – С4, обеспечивающее выигрыш в 60 ден.ед. Поскольку точно не известно, какую обстановку ожидать, то могла быть выбрана стратегия С1, дающая выигрыш в обстановке П4 всего 8 ден.ед. При этом потеря в величине выигрыша составит 60 – 8 = 52 ден.ед. Величины риска определяются следующими выражениями:
rij = 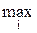 аij - аij = bj - aij,
аij - аij = bj - aij,
где аij – размер «выигрыша» при выборе i–й стратегии при j–м состоянии «природы»; bj - максимальный «выигрыш» для j–й обстановки; rij - величина риска при выборе i–й стратегии при j–й обстановке. Составим матрицу рисков
| П1 | П2 | П3 | П4 | |
| С1 | ||||
| С2 | ||||
| С3 | ||||
| С4 |
Матрица рисков дает возможность непосредственно оценить качество различных решений и установить, насколько полно реализуются в них существующие возможности достижения успеха при наличии риска. Например, основываясь на матрице игры, можно прийти к выводу, что решение С1 при обстановке П3 равноценно решению С3 при обстановке П2, поскольку выигрыш в обоих случаях равен 16 ден.ед. Однако риск при этом неодинаков и составляет соответственно 34 и 24 ден.ед.
Date: 2015-07-24; view: 468; Нарушение авторских прав