
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Матричные игры
|
|
Пусть игрок А имеет m чистых стратегий А1, А2, … Аi,…Аm, а игрок В имеет n чистых стратегий B1, B2, … Bj,…Bn. Такая игра называется игрой m х n. Если игрок А пользуется стратегией Аi, а игрок В пользуется стратегией Вj, то обозначим через аij выигрыш игрока А, если аij > 0, или проигрыш игрока А, если аij < 0. Очевидно, что – это одновременно проигрыш игрока В, если аij > 0, и выигрыш игрока В, если аij < 0.
Тогда мы можем привести игру к матричной форме, т.е. составить матрицу, которая называется платежной матрицей, или матрицей игры:
| В1 | В2 | … | Вj | … | Вn | |||
| А1 | а11 | а12 | … | а 1j | … | а 1n | ||
| а21 | а 22 | … | а 2j | … | а 2n | ||
| … | … | … | … | … | … | … | ||
| Аi | аi1 | а i2… | … | а ij | … | а in | ||
| … | … | … | … | … | … | … | ||
| Аm | аm1 | а m2 | … | а mj | … | а mn |
Каждая строка этой матрицы соответствует некоторой стратегии игрока А, а каждый столбец – некоторой стратегии игрока В.
Пример игры. Два игрока выкидывают на пальцах числа, причем четное число пальцев – это выигрыш игрока А, нечетное – проигрыш игрока А. Для простоты введем ограничение – игроки выкидывают от 1 до 3 пальцев.
Составим платежную таблицу:
| В1 | В2 | В3 | Вn | ||||
| -3 | -3 | |||||
| А2 | -3 | -5 | -5 | ||||
А3 | -5 | -5 | |||||
   max
i max
i
| |||||||
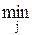
|
Проанализируем матрицу игры: для каждой чистой стратегии игрока А определим минимальный выигрыш, т.е. определим
ai = 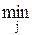 аij.
аij.
В нашем примере a1 = -3; a2 = -5; a3 = -5. Далее, среди полученных значений li-х определим максимальное
a = 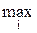 ai =
ai = 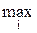
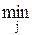 аij.
аij.
В нашем примере a = -3, т.е. игрок А проигрывает 3 очка. Это число a называется нижней ценой игры, а соответствующая ему стратегия называется максиминной. В нашем примере стратегия А1 максиминная, т.е. из всех наихудших ситуаций выбирают наилучшую. Эта величина (a) – гарантированный «выигрыш» игрока А, какую бы стратегию ни выбрал игрок В.
Меньше нижней цены игры игрок А никогда не «выиграет».
Игрок В старается максимально уменьшить свой проигрыш. Для этого определяется верхняя цена игры
b = 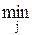 bj =
bj = 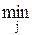
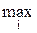 аij.
аij.
Соответствующая стратегия называется минимаксной. В нашем примере будет две минимаксных стратегии В1 и В2. При этом игрок В проигрывает 4 очка.
Теорема 1. В любой матричной игре справедливо неравенство a £ b, т.е. нижняя цена игры никогда не превосходит верхнюю.
Date: 2015-07-24; view: 391; Нарушение авторских прав
