Тема 6. Модели управления

Необходимость поставок сырья и производственного оборудования, удовлетворения запросов потребителей и создания разумного резерва запасных частей ставит задачи, которые можно различать по характеру спроса. Спрос может быть: детерминированным (т.е. предсказуемым с определенной точностью); случайным, но статистически устойчивым; случайным, но статистически неустойчивым (сезонные колебания); неизвестным.

Экономическая функция, оптимум которой отыскивается для случайного спроса, часто определяется как математическое ожидание общих затрат.

В задачах управления запасами рассматривают следующие факторы:

1) спрос на определенную продукцию, который либо является случайной во времени величиной, либо известен и определен;

2) наличие запаса этой продукции для удовлетворения спроса, его пополнение и восстановление; пополнение может быть нерегулярным, периодическим или осуществляться через некоторые интервалы времени;

3) затраты на ассигнования, страхование, хранение, а также убытки из-за неудовлетворенного спроса образуют экономическую функцию, которую нужно оптимизировать;

4) ограничения, определяемые факторами, связанными с задачей запасов.

Предположим, что интервал времени от заключения договора на пополнение до получения продукции равен нулю. В этом случае различают два основных метода простого уравнения запасами. Первый называется периодическим методом. Обозначим через Т период времени, в конце которого систематически производится пополнение запасов до максимально возможного уровня V_max. Тогда кривая изменения запаса имеет вид

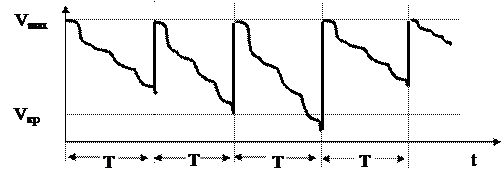Этот метод имеет недостаток, связанный с риском исчерпания запасов, что может повлечь за собой дорогостоящее управление, но его преимуществом является автоматизм.

Другой метод можно назвать релаксационным. Здесь количество вновь поступающей продукции постоянно, и равно разности между максимальным V_max и минимальным V_min уровнями запаса, но интервалы времени Т₁,Т₂,Т₃,…,Т_n не равны друг другу. В этом случае кривая изменения запаса имеет вид

В этой модели нет риска исчерпания запасов, управление более дешевое, но ее труднее автоматизировать.

Допустим, что задержка в пополнении (интервал времени между заключением договора и получением продукции) не зависит от объема получаемой продукции, т.е. постоянна и равна t. Метод управления запасами, при котором пополнение заказывается, когда запас достигает некоторой критической величины или уровня пополнения, называют «системой двух складов», или «S-s методом». Кривая изменения запаса для такого случая имеет вид

К затратам, связанным с организацией заказа и его реализацией, относятся расходы, производимые в связи с пополнением запасов начиная с поиска поставщика и оформления заказа и кончая оплатой всех услуг по доставке продукции на склад (расходы по размещению заказов, заключению договоров, расходы на связь, расходы по разъездам агентов снабжения, транспортные расходы, оплата стоимости погрузочно-разгрузочных операций и т.д.). Считается, что часть расходов, связанная с организацией заказов, зависит не от размера заказа, а от их количества за год.

Расходы по хранению запасов – сложный показатель, так как хранение запасов вызывает не только затраты, связанные с физическим присутствием продукции на складе, но и затраты вследствие вложения средств в запасы (организация хранения, устаревание, порча и др.).

Потери из-за дефицита имеют место в том случае, когда снабженческо-сбытовая организация несет материальную ответственность за то, что не может удовлетворить потребительский спрос из-за отсутствия запасов.

Модель 1. Допустим, фирма должна поставлять своим клиентам R изделий равномерно в течение интервала времени Т. Следовательно, спрос детерминированный. Нехватка товаров не допускается, т.е. штраф при неудовлетворительном спросе бесконечно велик: С_Н ® ¥. Переменные затраты складываются из следующих элементов: С_Х – стоимость хранения одного изделия в единицу времени; С_Z – затраты, связанные с организацией заказа (стоимость заказа).

Необходимо решить, как часто нужно организовывать заказ партий на склад фирмы и каким должен быть размер каждой партии.

Если V – размер партии заказа, t_Z - интервал времени между заказами партий, а S – полный спрос за время Т, то 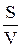– число партий за время Т и

t_Z = 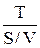= . (1)

Если интервал t_Z начинается, когда на складе имеется V изделий и заканчивается при отсутствии изделий, то V/2 – средний запас в течение t_Z, а затраты на хранение в интервале t_Z составят V/2 × C_X × t_Z.

Полная стоимость З_П создания запасов за время Т равна сумме стоимости хранения и стоимости заказа, умноженных на общее число партий за это время:

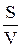З_П = ( t_Z + С_Z) , (2)

подставляя выражение для t_Z, получая:

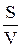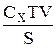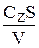З_П = ( × + С_Z) = + . (3)

С увеличение размера партий первое слагаемое этого выражения вырастает, а второе убывает. Суммируя эти зависимости, можно определить оптимальный размер партии заказа:

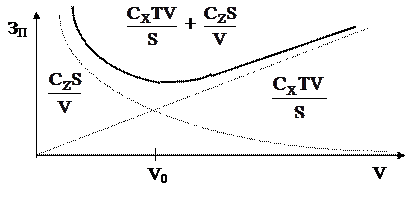Решение задачи управления запасами состоит в определении такого оптимального размера партии заказа V₀, при котором суммарная стоимость была бы наименьшей, т.е. нахождении экстремума функции общих ожидаемых расходов З_П.

Продифференцируем последнее выражение по V, получим

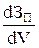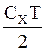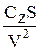= - . (4)

Если вторая производная положительна, то в точке перегиба функция имеет минимум, получим

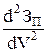= 2 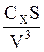> 0, следовательно, при V =V₀ имеем минимум функции.

Поскольку в точке экстремума первая производная должна быть равна нулю, то из условия 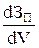= 0 найдем

V₀ = 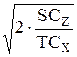. (6)

Подставим это выражение в (1) для получим оптимальное время между заказами

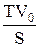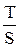
t_Z0 = = = 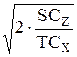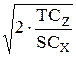. (7)

Подставим выражение (6) в (3), получим оптимальную (минимальную) величину затрат

З₀ = + 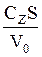= 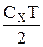× 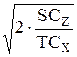+ 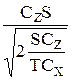= 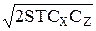. (8)

Пример. Фирма должна поставлять своим заказчикам 58000 единиц продукции в год. Поскольку получаемая продукция используется непосредственно на сборочной линии и заказчики не имеют для нее специальных складов, фирма-поставщик должна ежедневно отгружать дневную норму. В случае нарушения поставок фирма-поставщик рискует потерять заказ, поэтому нехватка продукции недопустима и штраф за это можно считать бесконечно большим. Хранение единицы продукции в месяц стоит 3 ден. ед. Стоимость заказа одной партии продукции составляет 420 ден.ед.

Требуется определить оптимальный размер партии заказа V₀, оптимальный период времени между заказами t_Z0 и вычислить минимум общих ожидаемых годовых затрат З₀.

В данном случае Т = 12 месяцев, S = 58000 единиц, C_X = 3 ден.ед./мес, C_Z = 420 ден.ед./партия. Подставим эти значения в выражения (6), (7) и (8):

V₀ = 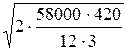= 1163 ед.,

t_Z0 = 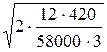= 0,24 месяца = 1 нед.,

З₀ = 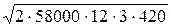= 41880 ден.ед./г.

Модель 2. Допустим, что превышение спроса над запасами допускается, т.е. штраф за нехватку продукции конечный. Кривая изменения запасов будет иметь вид

В этом случае интервал времени t_Z может состоять из t_X – времени, когда запас есть, и t_H – времени отсутствия запасов. На складе фирмы–поставщика до получения следующей партии пополнения запасов t_X = 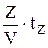, t_H = 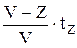, где Z – уровень запаса к началу периода.

Средний запас в течение t_X равен 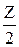, затраты на хранение за время t_X равны 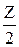× C_X × t_X. Средняя нехватка за время t_H равна 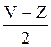, а штраф за время t_H составляет 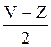× C_H × t_H.

Полные расходы за время Т равны сумме затрат на хранение, штрафа за нехватку и стоимости заказа

З_П = (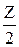 × C_X × t_X + 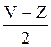× C_H × t_H + С_Z) × 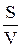. (9)

Подставляя сюда значения t_X, t_H и t_Z = TV/R, получая

З_П = 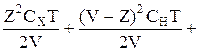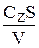. (10)

Из уравнения (10) можно найти оптимальные значения для V и Z:

V₀ = 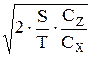× 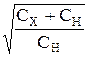; (11)

Z₀ = 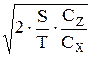× 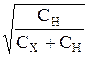; (12)

t_Z0 = 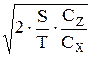× 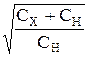; (13)

З₀ = 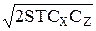× 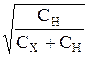. (14)

Пример. Пусть сохраняются все условия предыдущего примера, а штраф за нехватку C_H = 4 ден.ед. за одно изделие в месяц. Из выражений (11) и (14) получим

V₀ = 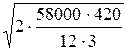× 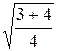= 1540 ед.,

Z₀ = 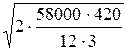× 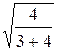= 879 ед.,

t_Z0 = 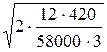× 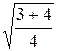= 0,317 месяцев = 1дек.,

З₀ = 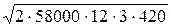× 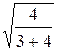= 31658 ден.ед.

Тема 7. Элементы и теория игр

Основные понятия теории игр

При решении задач в области экономики и управления производством в условиях неполноты и неточности информации возможны ситуации, когда необходимо принятие решений в условиях риска и неопределенности.

Предметом изучения теории игр являются ситуации, когда отсутствует полнота информации, а аппарат теории игр предназначен для выбора оптимальных решений в условиях неопределенности. Методы теории игр разработаны применительно к специфическим конфликтным ситуациям, которые обладают свойством многократной повторяемости. Целью теории игр является выработка рекомендаций по рациональному образу действия участников многократно повторяющегося конфликта. Под конфликтными ситуациями понимается положение, когда сталкиваются интересы двух и более сторон, причем выигрыш зависит от того, как поведут себя другие стороны. Математический анализ конфликта возможен при построении математической модели конфликта. Такая модель называется игрой. От реального конфликта игра отличается тем, что ведется по определенным правилам, которые участникам конфликта известны и строго выполняются. Игра называется парной, если в ней участвуют две стороны. Если в парной игре выигрыш одного из игроков равен проигрышу другого, то такая парная игра называется игрой с нулевой суммой. Конечной игрой называется игра с конечным числом стратегий. Стратегией называется совокупность правил, определяющих выбор варианта действия при каждом ходе в зависимости от сложившейся ситуации. Ходы бывают личные и случайные. При случайном ходе – выбор стратегии случайный. Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает ему максимальный средний выигрыш или минимальный средний проигрыш.

Date: 2015-07-24; view: 459; Нарушение авторских прав