Функции Уолша

Способов построения систем взаимно ортогональных функций достаточно много и они подробно изучены в математике. В последнее время, под влиянием методов обработки дискретных сигналов большое внимание уделяется ортонормированной системе функций Уолша, которые на отрезке своего существования [-T\2, +T\2] принимают значеня ±1.

Введем безразмерное время t/T=υ и будем обозначать, как это принято, k-ю функцию Уолша wal(k,υ).

Аналитическое описание данных функций достаточно сложно, однако идею построения этой системы легко продемонстрировать рисунком, на котором изображены графики нескольких первых функций Уолша.

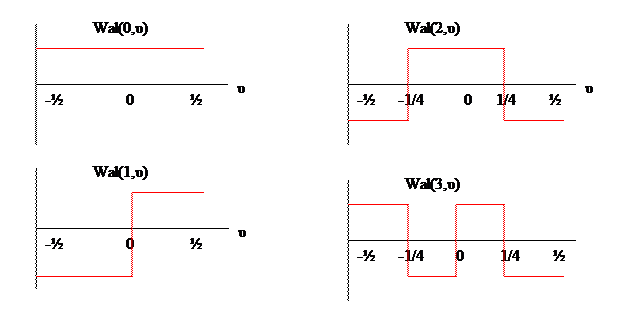
Ортогональность этих функций следует из принципа их построения и может быть проверена непосредственно. Например:

.

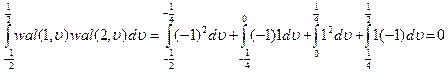Разложение сигнала с конечной энергией, заданного на отрезке [-T\2, +T\2], в обобщенный ряд Фурье по функциям Уолша имеет вид

.

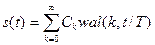В качестве примера найдем первые два коэффициента в разложении импульса треугольной формы.

На отрезке [-T\2, +T\2] разлагаемый сигнал

.

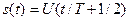Вычисляем коэффициенты обобщенного ряда Фурье:

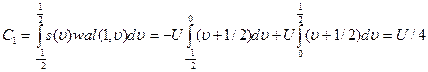
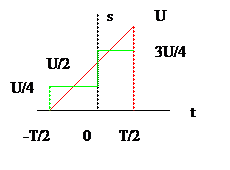
Итак, при аппроксимации колебания треугольной формы двумя первыми членами ряда по системе Уоша получается приближенное представление ступенчатой формы. Отметим, что с точки зрения энергетической норны уже такая грубая аппроксимация является удовлетворительной.

Действительно, энергия исходного сигнала

,

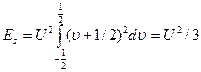в то время как энергия разности

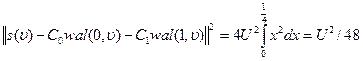
составляет лишь 1/16 или 6,25% от энергии аппроксимируемого сигнала.

Заключение

Рассмотренные в лекции методы статистического описания сигналов будут использованы в дальнейшем для описания информационных характеристик систем передачи сообщений в реальных каналах связи.

Разработал:

Доктор военных наук, профессор

А. Привалов

«» __________ 2010 года

[1] Случайный характер принимаемых сигналов связан также с искажения­ми и помехами, которые возникают при многолучевом распространении.

Date: 2015-07-24; view: 851; Нарушение авторских прав