Нормированное линейное пространство. Энергия сигнала

Для того, чтобы ответить на вопрос на сколько один сигнал больше другого, введем понятие, которое по своему смыслу соответствует длине вектора.

Длину вектора в математике принято называть нормой. Линейное пространство сигналов является нормированным, если каждому вектору s(t) € L однозначно сопоставлено число ||s|| - норма этого вектора, причем выполняются следующие аксиомы нормированного прстранства:

1. Норма не отрицательна, т.е. ||s||≥0. Норма ||s||=0 тогда и только тогда, если s=Ǿ.

2. Для любого числа α справедливо равенство ||sα||=|α| ||s||.

3. Если s(t) и p(t) – два вектора из L, то выполняется неравенство треугольника: ||s+p||≤||s||+||p||.

Можно предложить разные способы введения нормы сигналов. В технике связи чаще всего полагают, что вещественные аналоговые сигналы имеют норму: , при этом из двух возможных значений корня выбирается положительное.

Для комплексных сигналов норма

.

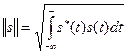Квадрат нормы носит название энергии сигнала

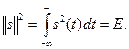
Именно такая энергия выделятся на резисторе с сопротивлением 1 Ом, если на его зажимах существует напряжение s(t).

Целесообразность определения энергии сигнала с использованием данной формулы целесообразно по следующим причинам:

- о величине сигнала в радиотехнике судят исходя из суммарного энергетического эффекта, например по количестув теплоты выделяемой на резисторе.

- Энергетическая норма оказывается не чувствительной к изменениям формы сигнала, может быть и значительным, но происходящих на коротких отрезках времени.

Линейное метрическое пространство вещественных сигналов с конечной величиной нормы носит название пространства функций с интегрируемым квадратом и кратко обозначается L₂.

Бесконечное семейство действительных функций

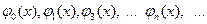(1)

называется ортогональным на отрезке [a,b], если

.

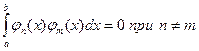А значит, их взаимная энергия также равна нулю.

При этом предполагается, что

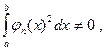
Т.е ни одна из функций семейства (1) тождественно не равна нулю.

Можно доказать, что если функции 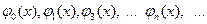ортогональны, то произвольная кусочно-непрерывная функция f(x), для которой выполняется условие

может быть представлена в виде суммы ряда

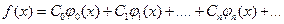(2)

Умножим обе части (2) на 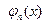и проинтегрируем в пределах [a,b]. В силу ортогональности в правой части остается одно слагаемое

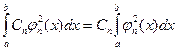
Отсюда

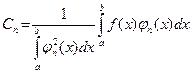(3)

Ряд (2) в котором коэффициенты С_п определены по формуле (3) называется обобщенным рядом Фурье по данному семейству { }.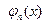

Совокупность коэффициентов С_п называется спектром сигнала и полностью определяет сигнал.

Говорят, что если на отрезке [a,b] задана бесконечная система ортогональных функций { 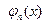}, обладающих единичными нормами:

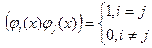
То в пространстве сигналов задан ортонормированный базис.

При заданном семействе { 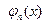} и фиксированном числе слагаемых ряда (2) он обеспечивает наилучшую аппроксимацию (в смысле минимума среднеквадратичной ошибки) данной функции f(x). Это означает, что среднеквадратическая ошибка Δ, под которой понимается величина

,

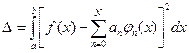Достигает минимума, когда коэффициенты ряда а_п=С_п.

Примерами функций 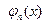являются:

1. Тригонометрические функции – синусы и косинусы;

2. Полиномы Чебышева;

3. Полиномы Эрмита;

4. Полиномы Лежандра;

5. Функции Уолша; и т.д.

Возможность представления сигналов посредством обобщенных рядов Фурье является фактором большого принципиального значения. Вместо того, чтобы изучать функциональную зависимость в несчетном множестве точек, мы получаем возможность характеризовать эти сигналы счетной системой коэффициентов ряда Фурье.

Date: 2015-07-24; view: 625; Нарушение авторских прав