
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Жордан өлшемді жиындар үшін екі еселі Риман интегралы. Қасиеттері
|
|
Жазықтықта шенелген Ω жиыны беріліп  нақты мәнді функциясы Ω жиынында анықталсын. Мақсатымыз - Ω жиыны бойынша алынған
нақты мәнді функциясы Ω жиынында анықталсын. Мақсатымыз - Ω жиыны бойынша алынған
 (1)
(1)
Интегралын анықтау. Ω жиыны үшбұрыш,дөңгелек т.б.фигуралар болу мүмкін.
(1)түріндегі интегралдың анықтамасы А тіктөртбұрышы бойынша анықталған Риман интегралына былай келтіріледі. Ω⊂R2 Жордан бойынша өлшенетін жиын болсын. Ω⊂А болатындай А тіктөртбұрышын алайық. R2 жиынында А жиынында да fΩ функциясын былай анықтайық:
fΩ(x,y)=  (2)
(2)
мұндағы теңдікті fΩ(x,y)=f(x,y)XΩ(x,y) көбейтінді түрінде бейнелеуге болады.
Егерде 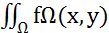 dxdy (3)
dxdy (3)
Интегралы бар болса, онда f(x,y) функциясы Ω жиынында Риман бойынша интегралданады, (3) санын  функцмясының Ω жиыны бойныша алынған интегралы деп,(1)символымен белгілейді.
функцмясының Ω жиыны бойныша алынған интегралы деп,(1)символымен белгілейді.
Ал fΩ(x,y) функциясы А жиынында интегралданбаса, онда 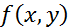 функциясы Ω жиынында интегралданбайды дейді.
функциясы Ω жиынында интегралданбайды дейді.
Ω жиынында  =1 тұрақты функциясы интегралдануы үшін Ωжиының Жордан бойынша өлшенетін жиын болуы қажетті де сонда
=1 тұрақты функциясы интегралдануы үшін Ωжиының Жордан бойынша өлшенетін жиын болуы қажетті де сонда

Теңдігі орындалады. Сол себептен де (1) интеграл анықтамасына Ω жиыны Жордан бойныша өлшенуі туралы деп қойылған.
1. Сызықтық қасиеті
Егер  және
және 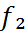 функциялары Жордан бойынша өлшенетін
функциялары Жордан бойынша өлшенетін  жиынында интегралданса, яғни
жиынында интегралданса, яғни
 Ω
Ω 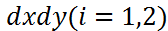
интегралдары бар болса, онда әр с₁ және с₂ нақты сандары үшін с₁ 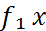 Ω және с₂
Ω және с₂ 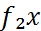 Ω функциялары, сонымен бірге олардың қосындысы да А тіктөртбұрышында интегралданып
Ω функциялары, сонымен бірге олардың қосындысы да А тіктөртбұрышында интегралданып
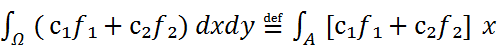 Ω
Ω  Ω
Ω  Ω
Ω  Ω
Ω  Ω
Ω  Ω
Ω 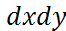
2. монотондық қасиеті
Егер Жордан бойынша өлшенетін өлшенетін  жиынында интегралданатын
жиынында интегралданатын  және
және 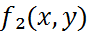 функциялары беріліп, әр
функциялары беріліп, әр  үшін
үшін  болса, онда
болса, онда

теңсіздігі орындалады.
Расында да, 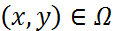 болғанда,
болғанда,  Ω
Ω  болып,
болып,
 Ω
Ω 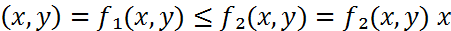 Ω
Ω 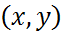
болады, ал 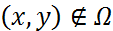 болғанда
болғанда  Ω
Ω 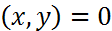 болып,
болып,
 Ω
Ω  Ω
Ω 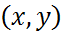
болады, демек, әр 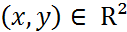 үшін
үшін
 Ω
Ω  Ω
Ω 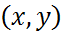
Сондықтан
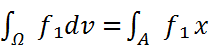 Ω
Ω 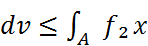 Ω
Ω 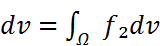
Сондай-ақ 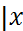 Ω
Ω 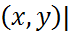 =
=  Ω
Ω 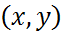 болғандықтан,
болғандықтан,
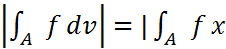 Ω
Ω  Ω
Ω 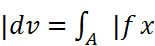 Ω
Ω 
4 теорема. Жазықтықта Жордан бойынша өлшенетін 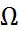 жиыны мен оның Жордан бойынша өлшенетін
жиыны мен оның Жордан бойынша өлшенетін  жиындарына жіктеу берілсін. Онда Ω жиынында анықталған f(x) шенелген функциясы Ω жиынында интегралдануы үшін оның әр
жиындарына жіктеу берілсін. Онда Ω жиынында анықталған f(x) шенелген функциясы Ω жиынында интегралдануы үшін оның әр  (k=1,…,N) жиынында интегралдануы қажетті де жеткілікті. Сонда
(k=1,…,N) жиынында интегралдануы қажетті де жеткілікті. Сонда
 =
=  (1)
(1)
Теңдігі орындалады.
Date: 2015-07-24; view: 1424; Нарушение авторских прав