
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Порядок выполнения работы. 1) Привести установку в строго горизонтальное положение с помощью опорных винтов и сферического уровня
|
|
1) Привести установку в строго горизонтальное положение с помощью опорных винтов и сферического уровня.
2) Установить лимбы балансировочных плоскостей на нуль и закрепить их.
3) Разогнать ротор и наблюдая за свободным вращением ротора при выбеге после перехода через резонанс, зафиксировать величину амплитуды А1. Опыт повторить 3 раза. Вычислить среднее арифметическое значение A1.
4) В произвольной плоскости 4 укрепить корректирующую массу mд; (создается дисбаланс тдrд)
Определить величину А2. Опыт повторить 3 раза и вычислить среднее арифметическое значение А2.
5) Повернуть плоскость 4 вместе с корректирующей массой на 180° и определить Аз.
6) По формулам определить величины Ад и µ.
7) Исходя из полученного дисбаланса, подобрать величины т1 и r1 и определить угол α.
8) Произвести балансировку ротора в плоскости 4. Рассчитанный противовес устанавливается в плоскости 4 (добавочные грузы снимаются) и производится контроль балансировки: три раза при резонансе измеряется остаточная амплитуда сбалансированного ротона A4. Так как одному значению косинуса соответствуют два угла α. Кроме того, при начальной установке добавочного груза (и наличии двух прорезей) не фиксируется его положение относительно нуля. Поэтому проверка сбалансированности делается при четырех углах: α, - α, 180° - α, 180° + α и определяется угол, при котором А4 имеет минимальное значение.
9) Определить остаточный дисбаланс ротора.
10) Результаты работы занести в журнал.
6. Принадлежности, необходимые для выполнения работы:
Калькулятор, авторучка.
ЛАБОРАТОРНАЯ РАБОТА № 5
КИНЕМАТИЧЕСКИЙ АНАЛИЗ ЗУБЧАТЫХ МЕХАНИЗМОВ
1. Цель работы
Приобретение навыков в определении передаточного отношения зубчатых механизмов и угловых скоростей звеньев.
2. Основные понятия
Кинематический анализ зубчатых механизмов заключается в определении передаточных отношений и угловых скоростей выходных и промежуточных звеньев по известным угловым скоростям входных звеньев.
Зубчатые механизмы могут быть плоскими и пространственными. У плоских механизмов звенья вращаются относительно параллельных осей. Пространственные механизмы применяют для передачи вращательного движения между пересекающимися или скрещивающимися осями.
Кроме того, зубчатые механизмы подразделяют на механизмы с неподвижными и подвижными осями вращения (эпициклические механизмы).
Зубчатые механизмы с неподвижными осями. Для выполнения кинематического анализа необходимо определить передаточное отношение зубчатой передачи. Передаточным отношением u12 называется отношение угловой скорости ω1 входного зубчатого колеса 1 к угловой скорости ω2 выходного зубчатого колеса 2:
u12 =ω1/ω2
У плоских цилиндрических механизмов передаточное отношение положительное, если зубчатые колеса вращаются в одном направлении, отрицательное, если колеса вращаются в разные стороны.
Угловые скорости колес, находящихся в зацеплении, обратно пропорциональны радиусам начальных окружностей rw, и числам зубьев z.
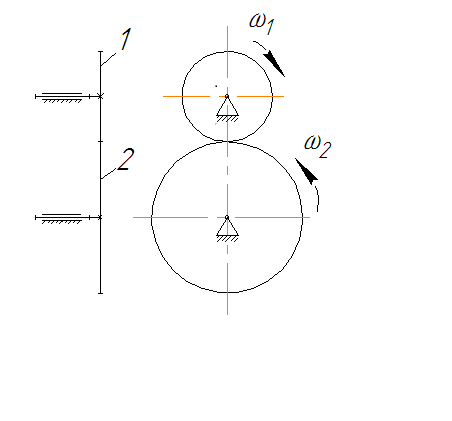
Таким образом, передаточное отношение для пары цилиндрических зубчатых колес внешнего зацепления (рис. 5.1, а)
u12 = ω1/ω2 = n1/n2 = - rw2/rwl = - z2/z1 (5.1)
внутреннего зацепления (рис. 5.1, б)
а б
Рис.5.1. Передача зубчатая (цилиндрическая):
а - внешнего зацепления; б - внутреннего зацепления
u12 = ω1/ω2 = n1/n2 = rw2/rwl = z2/z1 (5.2)
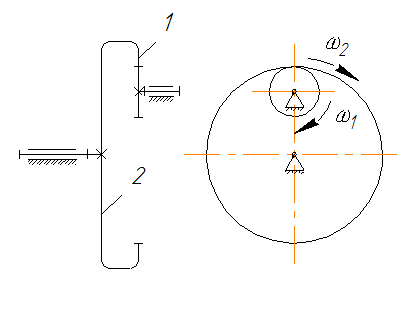
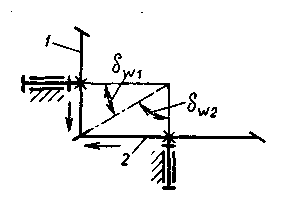
Конические зубчатые колеса (рис. 5.2) применяют для передачи вращательного движения между пересекающимися осями. Передаточное отношение этих механизмов
u12 = ω1/ω2 = n1/n2 = 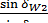 = - rw2/rwl = - z2/z1 (5.3)
= - rw2/rwl = - z2/z1 (5.3)
На кинематической схеме направление вращения зубчатых колес можно показать стрелками.
|
|
Рис 5.2 Передача зубчатая с пересекающимися валами (коническая)
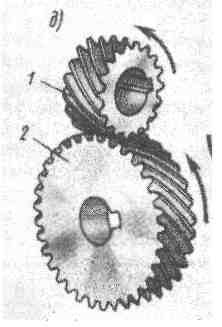
Гиперболоидный зубчатый механизм используют для передачи вращательного движения между скрещивающимися осями. Если начальные поверхности колес— круглые цилиндры, передача называется винтовой (рис. 5.3). Передаточное отношение винтовой передачи
u12 = ω1/ω2 = n1/n2 = 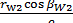 = z2/z1, (5.4)
= z2/z1, (5.4)
где βW1 и βW2 - углы наклона винтовых линий по начальным цилиндрам.
|
|
Рис 5.3 Передача зубчатая со скрещивающимися валами (винтовая)

|
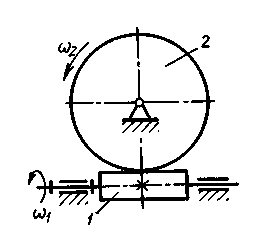
|
Рис 5.4 Передача червячная с цилиндрическим червяком
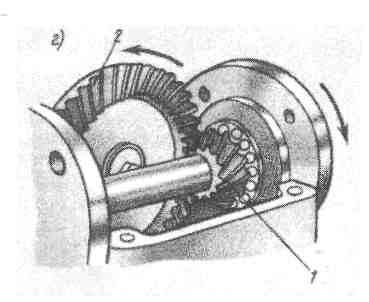
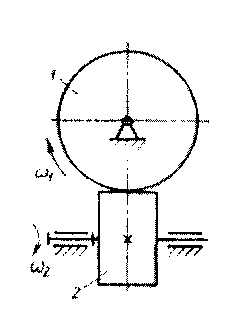
Червячная зубчатая передача (рис.5.4) - частный случай гиперболоидной. Угол скрещивания осей в большинстве случаев равен 90°. Червяком называется косозубое зубчатое колесо, линия зубьев которого делает один оборот или более вокруг его оси.
Числом зубьев z1 червяка называют число заходов винтовой линии. Передаточное отношение червячной передачи
u12 = ω1/ω2 = n1/n2 = z2/z1 (5.5)
Направление вращения червячного колеса зависит от направлений вращения червяка и винтовой линии.
Обычно для одной пары колес u12 = 5÷7 для механических передач и u12 = 10÷12 для ручных передач.
Машиностроительная практика часто требует значительно больших передаточных отношений. Поэтому для осуществления их применяются сложные зубчатые механизмы, состоящие из нескольких пар зубчатых колес.
Зубчатые механизмы, служащие для уменьшения числа оборотов ведомого вала по сравнению с ведущим, называются редукторами, а механизмы, служащие для увеличения числа оборотов ведомого вала, называются мультипликаторами.
Сложные зубчатые механизмы применяются также для передачи вращения от ведущего вала к ведомому с различными (по постоянными) передаточными отношениями. Такие зубчатые механизмы называются коробками скоростей.
Рассмотрим определение передаточных отношений сложных зубчатых механизмов.
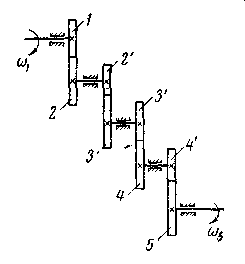
На рис. 5.5 изображена схема сложного зубчатого механизма, геометрические оси колес которого неподвижны (валы вращаются в неподвижных подшипниках). Механизм состоит из ведущего вала 1, на котором неподвижно сидит колесо z1, промежуточных валов 2, 3 и 4, на которых сидят неподвижно по два зубчатых колеса последовательно z2, z'2, и z'3 и z3, z4 и z4', ведомого вала 5, на котором неподвижно посажено колесо z5. Передача вращательного движения от ведущего вала 1 к ведомому 5 осуществляется последовательно при помощи четырех пар (или четырех ступеней) зубчатых колес.
Такие механизмы называются многоступенчатыми.
|
Согласно общему определению,
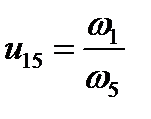
Передаточные отношения отдельных ступеней равны:
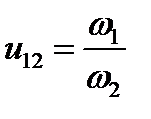 ;
; 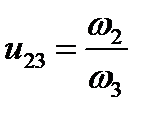 ;
;
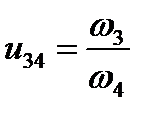 ;
; 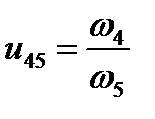
| Рис. 5.5. Многоступенчатая зубчатая передача |
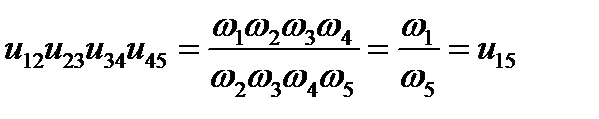
или окончательно
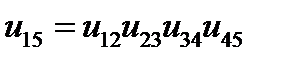 (5.6)
(5.6)
Таким образом, передаточное отношение многоступенчатого зубчатого механизма равно произведению передаточных отношений простых зубчатых механизмов (отдельных ступеней), входящих в его состав.
В общем случае, когда передача движения осуществляется с помощью п пар зубчатых колес, количество валов равно n+1. Передаточное отношение в этом случае будет
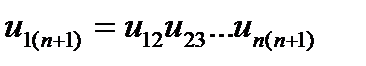 (5.7)
(5.7)
При пользовании этим уравнением для плоского зубчатого механизма следует учитывать знак передаточного отношения.
На практике для определения знака передаточного отношения плоских зубчатых механизмов проще пользоваться формулой
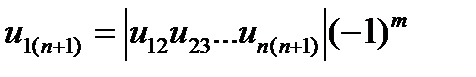 (5.8)
(5.8)
Здесь передаточные отношения берутся по абсолютной величине, а знак их определяется величиной 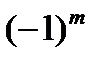 , где m — количество простых зубчатых передач с внешним зацеплением (так как только внешнее зацепление изменяет направление вращения).
, где m — количество простых зубчатых передач с внешним зацеплением (так как только внешнее зацепление изменяет направление вращения).
Передаточное отношение плоского многоступенчатого зубчатого механизма, выраженное через количество зубьев зубчатых колес, в общем случае равно
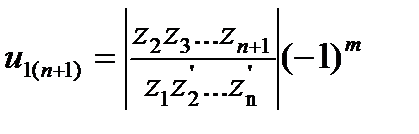 (5.9)
(5.9)
Следует отметить, что во многих задачах номера колес и валов обозначены иначе, чем на нашем рисунке. Однако это значения не имеет. Надо только всегда внимательно смотреть, между какими колесами осуществляется зацепление.
Рассмотрим сложный зубчатый механизм, в котором на промежуточных валах расположено не по два, а по одному колесу (рядовое соединение колес) (рис. 5.6).
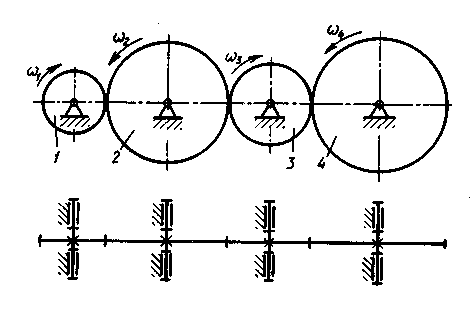
|
Рис. 5.6. Схема рядового соединения зубчатых колес
Передача вращательного движения от ведущего вала 1 к ведомому 4 осуществляется при помощи трех простых зубчатых механизмов z1-z2, z2-z3, z3-z4. Передаточное отношение этого сложно го механизма можно определить по формуле (5.8):
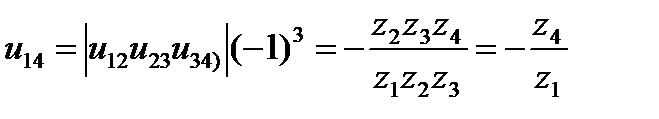 .
.
Как видно, на абсолютную величину передаточного отношения количество зубьев промежуточных зубчатых колес не оказывает никакого влияния. Оно влияет только на знак передаточного отношения. Такие промежуточные колеса называются паразитными. Они применяются для изменения направления вращения ведомого вала, а также для передачи вращения между валами, расположенными на сравнительно большом расстоянии.
При определении величины передаточного отношения паразитные колеса учитывать не следует. Для определения направления необходимо учесть только количество простых передач с внешним зацеплением m. Для нашего случая
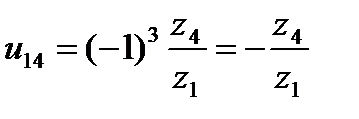 .
.
Указанный способ определения направления вращения ведомого вала (5.9) приемлем только для плоских зубчатых механизмов, т. е. дня механизмов, состоящих из цилиндрических зубчатых колес.
Для пространственных зубчатых механизмов способ определения направления вращения ведомого (и других) вала заключается в следующем.
Пусть пространственный зубчатый механизм состоит из различных пар конических зубчатых колес (рис.5.7). Проведем на колесе 1 стрелку таким образом, чтобы она совпадала с направлением движения зубьев, расположенных ближе к нам (вниз). Тогда на колесе 2, которое находится в зацеплении с колесом 1, движение зубьев (также расположенных ближе к нам) будет направлено влево,
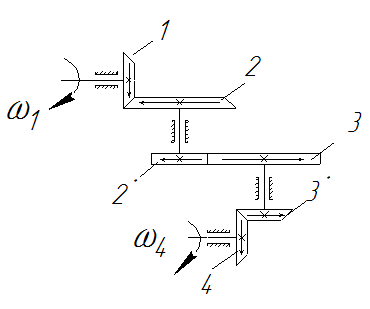
Рис. 5.7. К определению знака передаточного отношения многоступенчатого зубчатого механизма, в состав которого входят конические колеса
следовательно, стрелку на колесе 2 направляем влево (как видно, стрелки на колесах 1 и 2 направлены друг к другу). Также влево направляем стрелку на колесе 2', так как оно сидит на одном валу с колесом 2. Па колесе 3, которое находится в зацеплении с колесом 2', стрелку направляем в противоположную сторону — вправо (таким образом, стрелки на второй паре колес направлены друг от друга). На колесе 3' стрелку также направляем вправо, так как колеса 3 и 3' сидят на одном валу. На колесе 4, которое находится в зацеплении с колесом 3', стрелку проводим так, чтобы стрелки на этих колесах были направлены друг от друга, т. е. вниз. Далее, сравнивая направление стрелок на колесах 1 и 4, видим, что они оба имеют одно направление (вниз), следовательно, ведущий и ведомый валы вращаются в одном направлении.
Эпициклические зубчатые механизмы. Особенность эпициклических механизмов - наличие зубчатых колес (сателлитов) с движущимися геометрическими осями. Эпициклические механизмы с одной степенью свободы, имеющие неподвижное колесо, называют планетарными редукторами или мультипликаторами (рис. 5.8), а механизмы с числом степеней свободы W ≥ 2, которые обычно не имеют неподвижного колеса, — дифференциальными механизмами.
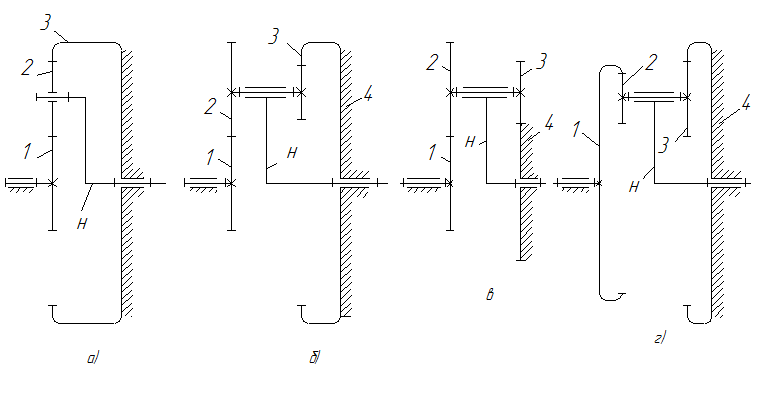
Рис 5.8. Схемы планетарных зубчатых механизмов
Угловые скорости звеньев планетарного редуктора связаны передаточным отношением
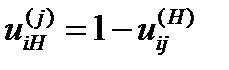 (5.10)
(5.10)
где 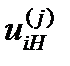 — передаточное отношение от i-ro колеса к водилу Н при неподвижном j-м колесе;
— передаточное отношение от i-ro колеса к водилу Н при неподвижном j-м колесе;  — передаточное отношение от i-ro колеса j-му в обращенном механизме при неподвижном водиле Н.
— передаточное отношение от i-ro колеса j-му в обращенном механизме при неподвижном водиле Н.
Например, для планетарного редуктора (см. рис. 5.8, б) при входном колесе 1 формула (5.10) имеет вид
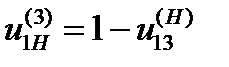 (5.11)
(5.11)
а при входном звене Н
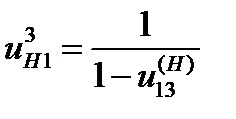 , (5.12)
, (5.12)
где 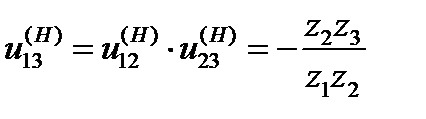 .
.
В таблице 5.1 приведены формулы для определения передаточных отношений типовых планетарных механизмов.
Таблица 5.1
Формулы для определения передаточных отношений
типовых планетарных механизмов
| Передаточные отношения | Тип а | Тип б | Тип в | Тип г |
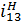
| 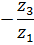
| 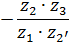
| 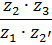
| 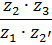
|
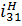
| 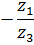
| 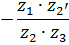
| 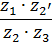
| 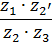
|
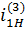
| 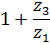
| 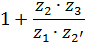
| 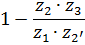
| 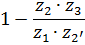
|
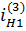
| 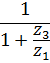
| 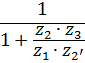
| 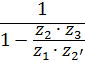
| 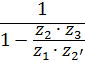
|
| 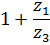
| 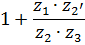
| 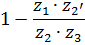
| 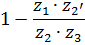
|
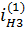
| 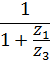
| 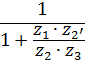
| 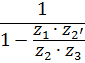
| 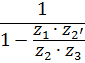
|
Date: 2015-07-24; view: 646; Нарушение авторских прав