
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Статическое и полное конструктивное уравновешивание ротора. Ознакомиться спроблемой конструктивного уравновешивания вращающегося тела типа ротор, получить навыки расчета схемы уравновешивания и экспериментальной
|
|
Цель работы
Ознакомиться спроблемой конструктивного уравновешивания вращающегося тела типа ротор, получить навыки расчета схемы уравновешивания и экспериментальной
ее проверки.
Основные понятия
При проектировании машин по конструктивным и технологическим соображениям вращающиеся звенья часто приходится выполнять с приливами, углублениями и другими элементами, способствующими смещению центра масс звена с оси вращения и наклону главной центральной оси инерции звена к оси вращения. Наглядным примером таких звеньев могут служить коленчатые валы. Каждое колено вала имеет центр масс, смещенный по отношению к оси вращения вала. Иногда автоматически (например, в некоторых типах многорядных двигателей внутреннего сгорания) удается разместить центр масс вала на оси вращения. Однако в этом случае главная центральная ось инерции по-прежнему может не совпадать с осью вращения.
Смещение центра масс или угловое смещение главной центральной оси инерции являются причиной возникновения неуравновешенных центробежных сил инерции и вызванных ими моментов сил инерции, которые являются причиной дополнительных реакций в опорах и вибраций механизма и машины, что, как правило, недопустимо.
С учетом этого уже на стадии проектирования звено конструируют таким образом, чтобы оно теоретически было полностью уравновешено. Эту задачу решают путем расчета специальных противовесов.
Противовес – это дополнительная масса, устанавливаемая на звено механизма (машины) для создания силы инерции, участвующей в уравновешивании механизма или масс механизма.
Точечные массы звеньев, силы инерции которых вызывают дополнительные нагрузки на опоры, называют неуравновешенными массами. Устранение или уменьшение дополнительных динамических нагрузок на опоры механизма от сил инерции звеньев называют уравновешиванием масс.
Различают три вида уравновешенности ротора: статическую, динамическую и полную. Ротор считается статически уравновешенным, если центр его масс лежит на оси вращения, т.е. главный вектор сил инерции Ри равен нулю, т.е.
Ри = ω2Σmiri,
где ω - угловая скорость вращения звена;
miri - статический дисбаланс.
Так как ω2 ≠0, то Σmiri =0.
Условием динамической уравновешенности является совпадение главной центральной оси инерции с осью вращения
или равенство нулю главного момента сил инерции Ми = О
Ми =co2∑mirjIi
где li, - расстояние от неуравновешенной массы до плоскости приведения;
mirjIi - динамический дисбаланс.
Ми = 0 или ∑mirjIi = 0
Выполнение обоих вышеназванных условий обеспечивает полную уравновешенность ротора.
Ри = 0, Ми = 0
∑mirjIi = 0∑mirjIi = 0
Неуравновешенные массы при конструктивном уравновешивании можно считать заданными, так как их можно вычислить, зная геометрические параметры звена и плотность материала, из которого оно изготовлено.
Пусть имеется модель ротора (рис. 3.1), в плоскостях которого 1,2, и 3, перпендикулярных оси вращения, имеются неуравновешенные массы т1, т2 и т3. Положения неуравновешенных масс в плоскостях заданы радиус-векторами r1, r2, r3. Положение плоскостей 1, 2, и 3 относительно плоскости приведения определяется соответственно координатами l1, l2, l3. Противовесы устанавливаются в плоскости 1 и плоскости 11, расстояния между ними l1-11 (плоскости приведения).
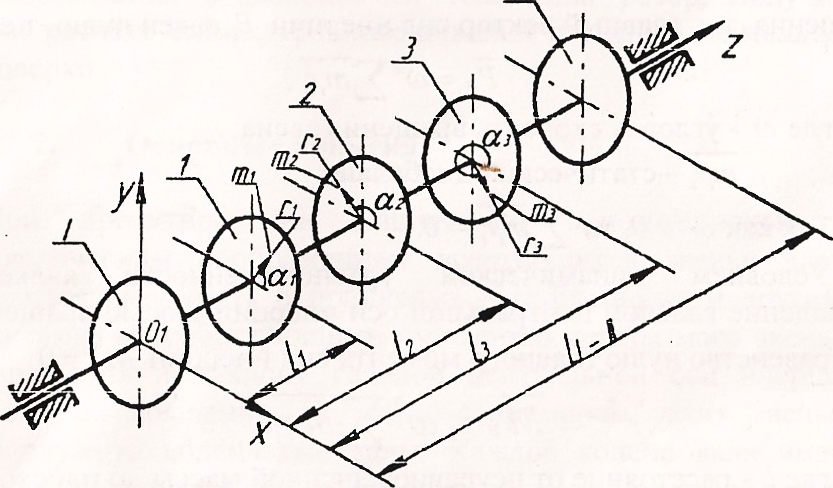
Рис. 3.1. Расчетная схема установки
Обозначим массы противовеса при статическом уравновешивании через тn, а радиус - векторы, определяющие положения их центров тяжести, через rn. Тогда условием уравновешенности ротора будет:
∑mirj + mnrn =0 (3.1)
При полном уравновешивании ротора массы противовесов, устанавливаемых в плоскостях 1 и 11, обозначим m1 и т11, а радиус - векторы, определяющие положения их центров тяжести, через r1и r2. Тогда условиями полного уравновешивания будут:
∑mirj + m1r1+ m11r11 =0 (3.2)
∑mirjli + m11r11l11 =0 (3.3)
При аналитическом решении этой задачи уравнение 3.1 развернется в два уравнения проекций на оси координат, а уравнение 3.2 и 3.3 - в четыре уравнения проекций на оси координат.
Более наглядным при выполнении студенческих лабораторных работ является графический метод.
Определение величины и положения противовеса графическим методом при статическом уравновешивании производится построением векторного многоугольника по уравнению 3.1 (рис. 3.2). Замыкающий вектор многоугольника определит собою произведение массы противовеса на радиус его расположения. Задавшись одной величиной (массой), можно определить вторую величину (радиус). Направление радиус-вектора противовеса определится углом аn, измеряемым непосредственно по чертежу.
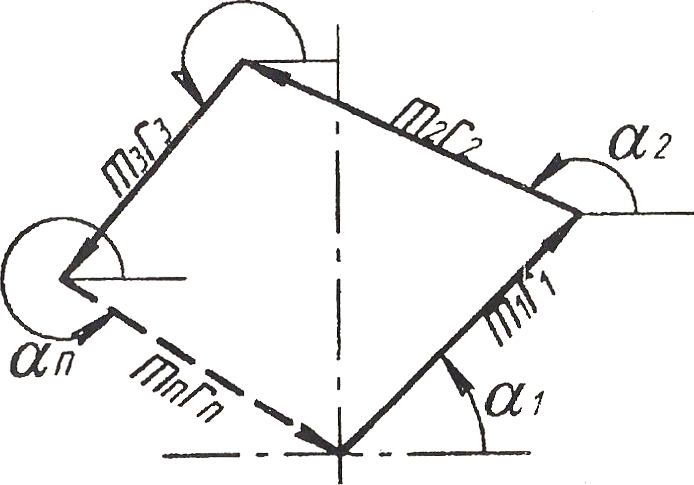
Рис. 3.2. Статическое уравновешивание ротора
При полном уравновешивании вначале строится векторный многоугольник динамических дисбалансов уравнению 3.3. Векторы моментов инерции при этом удобно повернуть на 90° до совпадения их с направлением векторов сил. Модуль вектора замыкающего многоугольника будет равен произведению m11r11l1-11 (рис.3.3, а), где l1-11 - расстояние между плоскостями
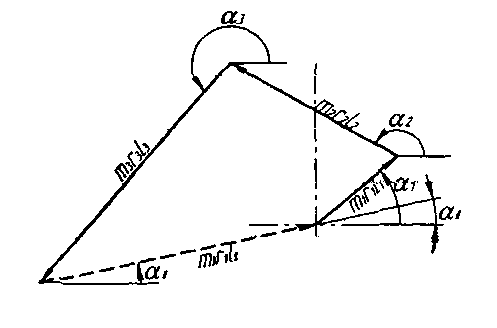
| а) |
| б) |
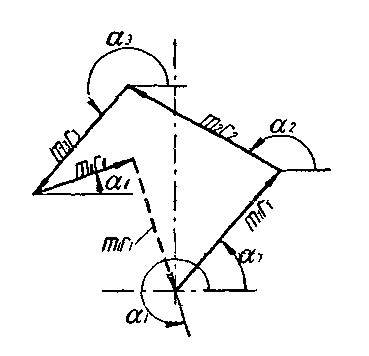
|
Рис 3.3. Полное уравновешивание ротора
(а) динамическое уравновешивание; (б) статическое уравновешивание
Date: 2015-07-24; view: 499; Нарушение авторских прав