Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Комбинаторика и бином Ньютона
|
|
1) Число перестановок из n элементов находится по формуле:
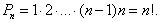 2) Число размещений из n элементов по m находится по формуле:
2) Число размещений из n элементов по m находится по формуле:
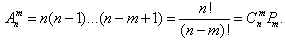 3) Число сочетаний из n элементов по m находится по формуле:
3) Число сочетаний из n элементов по m находится по формуле:
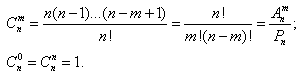 4) Справедливы следующие свойства сочетаний:
4) Справедливы следующие свойства сочетаний:
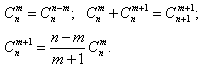 5) Формула бинома Ньютона имеет вид:
5) Формула бинома Ньютона имеет вид:
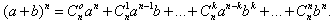 Сумма показателей чисел a и b равна n.
Сумма показателей чисел a и b равна n.
| 6) (k+1)-й член находится по формуле:
 7) Число сочетаний
7) Число сочетаний 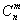 также можно найти по треугольнику Паскаля.
Треугольник Паскаля (до n=7): также можно найти по треугольнику Паскаля.
Треугольник Паскаля (до n=7):
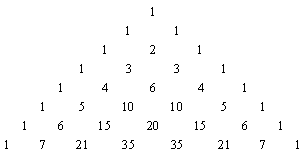 8) Сумма биномиальных коэффициентов равна 2n.
9) Чтобы найти биномиальный коэффициент следующего члена, нужно биномиальный коэффициент предыдущего члена умножить на показатель числа a и разделить на кол-во предыдущих членов.
8) Сумма биномиальных коэффициентов равна 2n.
9) Чтобы найти биномиальный коэффициент следующего члена, нужно биномиальный коэффициент предыдущего члена умножить на показатель числа a и разделить на кол-во предыдущих членов.
|
Вопрос 2 билет 24
Билет 28
Определение: Определенный интеграл от функции 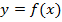 по отрезку
по отрезку 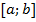 – это предел интегральных сумм
– это предел интегральных сумм 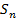 при
при 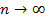 .
.
Обсудим каждый элемент введенного определения:
a, b – пределы интегрирования.
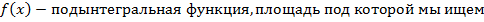
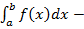 площадь криволинейной трапеции подынтегральной функции
площадь криволинейной трапеции подынтегральной функции 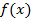 в пределах от
в пределах от 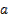 до
до 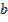
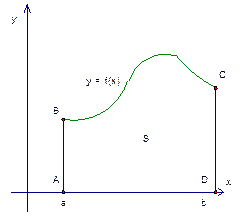
5. Теорема о вычислении определенного интеграла
Теорема: Если 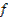 – непрерывная и неотрицательная на отрезке
– непрерывная и неотрицательная на отрезке 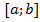 функция, а
функция, а 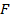 – ее первообразная на этом отрезке, то площадь
– ее первообразная на этом отрезке, то площадь 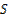 соответствующей криволинейной трапеции равна приращению первообразной на отрезке
соответствующей криволинейной трапеции равна приращению первообразной на отрезке 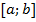 , то есть:
, то есть:
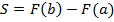
Обсудим полученную формулу (рис. 3).
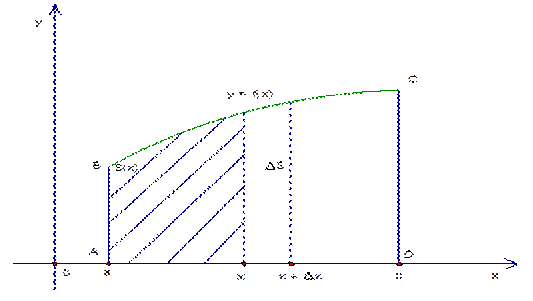
7. Формула Ньютона-Лейбница
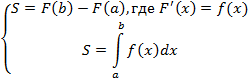
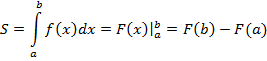
 – непрерывная на отрезке
– непрерывная на отрезке  .
.
Вопрос 2 билет 20
Билет 29
Тангенс, котангенс
Определения обратных тригонометрических функций
Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin x, при заданном 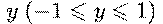 , имеет бесконечно много корней. Действительно, в силу периодичности sin, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны. Чтобы с ними было проще работать, вводят понятие их главных значений. Например, если для синуса y = sin x, если ограничить аргумент x интервалом
, имеет бесконечно много корней. Действительно, в силу периодичности sin, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны. Чтобы с ними было проще работать, вводят понятие их главных значений. Например, если для синуса y = sin x, если ограничить аргумент x интервалом 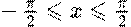 , то на этом интервле функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y.
, то на этом интервле функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y.
Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
Арксинус ( y = arcsin x ) это функция, обратная к синусу (x = sin y), имеющая область определения 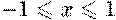 и множество значений
и множество значений 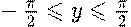 .
.
Арккосинус ( y = arccos x ) это функция, обратная к косинусу (x = cos y), имеющая область определения 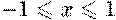 и множество значений
и множество значений 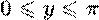 .
.
Арктангенс ( y = arctg x ) это функция, обратная к тангенсу (x = tg y), имеющая область определения  и множество значений
и множество значений 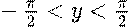 .
.
Арккотангенс ( y = arcctg x ) это функция, обратная к котангенсу (x = ctg y), имеющая область определения  и множество значений
и множество значений 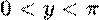 .
.
Графики обратных тригонометрических функций
Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x. См. разделы Синус, косинус, Тангенс, котангенс.
y = arcsin x
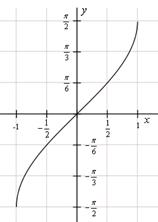
y = arccos x
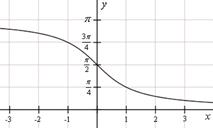
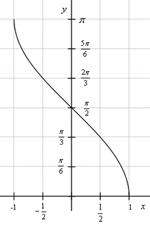
y = arctg x
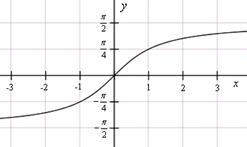
y = arcctg x
вопрос 2 билет 23
билет 30
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием можно использовать для нахождения производных степенных, рациональных и некоторых иррациональных функций.
Рассмотрим этот подход более детально. Пусть дана функция y = f (x). Возьмем натуральные логарифмы от обеих частей:Ln(y) =ln f (x). 
Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x
(ln y) ′ =(ln f (x)) ′,⇒1 yy ′ (x)=(ln f (x)) ′. 
Отсюда видно, что искомая производная равна
y ′= y (ln f (x)) ′= f (x)(ln f (x)) ′. 
Такая производная от логарифма функции называется логарифмической производной.
Данный метод позволяет также эффективно вычислять производные показательно-степенных функций, то есть функций вида
y = u (x) v (x), 
где u (x) и v (x) − дифференцируемые функции от x.
Вопрос 2
ТЕОРЕМА:
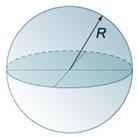
О сечении сферы плоскостью
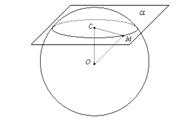
Сечение сферы плоскостью есть окружность.
Пусть плоскость α пересекает сферу W(O,R). Из центра O опустим перпендикуляр OC на плоскость α.
Соединим произвольную точку M линии пересения плоскости α со сферой W(O,R) с точками O и C. Т.к. OC ⊥ α, то OC ⊥ CM.
В прямоугольном треугольнике ∆OCM CM2 = OM2 - OC2. Т.к. OM и OC - величины постоянные, то и CM - величина постоянная. Таким образом все точки линии пересечения плоскости α и сферы W(O,R) равноудалены от точки C, поэтому эта линия пересечения является окружностью с центром в точке C и радиусом r = CM.
СЛЕДСТВИЕ:
Сечение шара плоскостью есть круг, а основание перпендикуляра проведенного из центра шара к пересекаемой плоскости есть центр круга, полученного в сечении.
Сфера − это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы). Расстояние между любой точкой сферы и ее центром называется радиусом. Геометрическое тело, ограниченное сферой, называется шаром.