
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формула вычисления объема шара
|
|
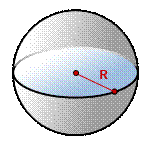
R- радиус шара
π ≈ 3,14
Объем шара, (V):
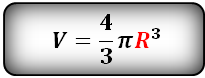
Билет 12
 Числовыми характеристиками случайных величин являются математическое ожидание и дисперсия, а так же и моменты случайных величин
Математическое ожиданием М(Х) называется средняя величина возможных значений случайных величин, взвешенных по их вероятности. Выражается формулой:
Свойство 1. Мат. ожидание постоянной равно этой постоянной.
Свойство 2. Мат. ожидание суммы случайных величин равно сумме их мат. ожиданий:
Из этого свойства следует следствие:
Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий:
Свойство 3. Математическое ожидание произведения независимых случайных величин Х и Y равно произведению математических ожиданий этих вел. M(XY)=M(X)·(M)Y.
Следствие. Постоянный множитель можно вынести за знак математических ожидания: М(сХ) = сМ(Х)
Дисперсией называется математическое ожидание квадрата отклонения случайных величин от математического ожидания:
D[Х]=M[X-M(X)]2
Свойство 1. Дисперсия постоянной величины равна нулю.
Свойство 2. постоянную величину можно вынести за знак дисперсии, предварительно возведя ее в квадрат:
D(cX) = c2D(X)
Свойство 3. Дисперсия суммы независимых случайных величин Х и Y равна сумме их дисперсий:
D(X+Y) = D(X) + D(Y), от сюда следствие:
если х1, х2,..., хn - случайные величины, каждая из которых независима от суммы остальных, то
D(X1+X2+...+Xn) = D(X1) + D(X2)+...+D(Xn).
Моментом k -порядка называется математическое ожидание k -й степени отклонения случайной величины Х от некоторой постоянной с.
Если в качестве с берется нуль, моменты называются начальными
νk = М(Х)k
Если с = М(Х), то моменты называются центральными
μ = M[X – M(X)]k
вопрос 2. Билет номер1
билет13
Тригонометрические функции
Основными тригонометрическими функциями являются функции y=sin(x), y=cos(x), y=tg(x), y=ctg(x). Рассмотрим каждую из них в отдельности.
Y = sin(x) Числовыми характеристиками случайных величин являются математическое ожидание и дисперсия, а так же и моменты случайных величин
Математическое ожиданием М(Х) называется средняя величина возможных значений случайных величин, взвешенных по их вероятности. Выражается формулой:
Свойство 1. Мат. ожидание постоянной равно этой постоянной.
Свойство 2. Мат. ожидание суммы случайных величин равно сумме их мат. ожиданий:
Из этого свойства следует следствие:
Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий:
Свойство 3. Математическое ожидание произведения независимых случайных величин Х и Y равно произведению математических ожиданий этих вел. M(XY)=M(X)·(M)Y.
Следствие. Постоянный множитель можно вынести за знак математических ожидания: М(сХ) = сМ(Х)
Дисперсией называется математическое ожидание квадрата отклонения случайных величин от математического ожидания:
D[Х]=M[X-M(X)]2
Свойство 1. Дисперсия постоянной величины равна нулю.
Свойство 2. постоянную величину можно вынести за знак дисперсии, предварительно возведя ее в квадрат:
D(cX) = c2D(X)
Свойство 3. Дисперсия суммы независимых случайных величин Х и Y равна сумме их дисперсий:
D(X+Y) = D(X) + D(Y), от сюда следствие:
если х1, х2,..., хn - случайные величины, каждая из которых независима от суммы остальных, то
D(X1+X2+...+Xn) = D(X1) + D(X2)+...+D(Xn).
Моментом k -порядка называется математическое ожидание k -й степени отклонения случайной величины Х от некоторой постоянной с.
Если в качестве с берется нуль, моменты называются начальными
νk = М(Х)k
Если с = М(Х), то моменты называются центральными
μ = M[X – M(X)]k
вопрос 2. Билет номер1
билет13
Тригонометрические функции
Основными тригонометрическими функциями являются функции y=sin(x), y=cos(x), y=tg(x), y=ctg(x). Рассмотрим каждую из них в отдельности.
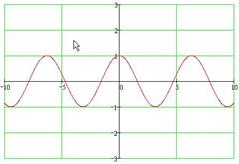
Y = sin(x)
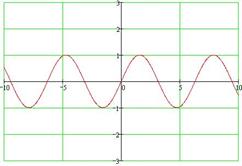 График функции y=sin(x). График функции y=sin(x).
 Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным 2*π.
Y = cos(x)
График функции y=cos(x).
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным 2*π.
Y = cos(x)
График функции y=cos(x).
 Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция четная.
4.Функция периодическая с наименьшим положительным периодом равным 2*π.
Y = tg(x)
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция четная.
4.Функция периодическая с наименьшим положительным периодом равным 2*π.
Y = tg(x)
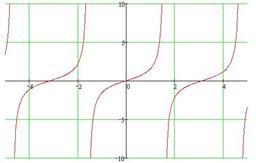 График функции y=tg(x). График функции y=tg(x).
 Основные свойства
1. Область определения вся числовая ось, за исключением точек вида x=π/2 +π*k, где k – целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
Y = ctg(x)
Основные свойства
1. Область определения вся числовая ось, за исключением точек вида x=π/2 +π*k, где k – целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
Y = ctg(x)
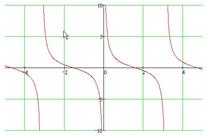 График функции y=ctg(x).
Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=π*k, где k – целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
Параллелепипед — это четырёхугольная призма, все грани которой являются параллелограммами.
Параллелепипеды — особая группа призм.
Как видно на данных рисунках, объёмные рисунки прямых параллелепипедов практически не отличаются.
У параллелепипеда 12 рёбер и 6 граней.
Виды параллелепипедов График функции y=ctg(x).
Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=π*k, где k – целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
Параллелепипед — это четырёхугольная призма, все грани которой являются параллелограммами.
Параллелепипеды — особая группа призм.
Как видно на данных рисунках, объёмные рисунки прямых параллелепипедов практически не отличаются.
У параллелепипеда 12 рёбер и 6 граней.
Виды параллелепипедов
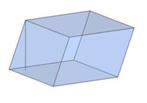 Наклонный
Наклонный
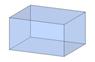 Прямой
Виды прямых параллелепипедов
Прямой параллелепипед, основание — параллелограмм
Прямой
Виды прямых параллелепипедов
Прямой параллелепипед, основание — параллелограмм
 Прямоугольный параллелепипед, основание — прямоугольник
Специальные случаи прямоугольного параллелепипеда
Прямоугольный параллелепипед, основание — прямоугольник
Специальные случаи прямоугольного параллелепипеда
 Правильная четырёхугольная призма, основание — квадрат, высота призмы не обязательно равна стороне основания
Правильная четырёхугольная призма, основание — квадрат, высота призмы не обязательно равна стороне основания
 Куб, все рёбра куба равны, все грани — квадраты
Секущая плоскость может рассекать параллелепипед по-разному, из-за чего сечением может являться 1) треугольник, 2) четырехугольник, 3) пятиугольник, 4) шестиугольник.
Рассмотрим случай, когда сечением параллелепипеда оказывается пятиугольник. При построении сечения руководствуемся правилом, согласно которому отрезки, по которым секущая плоскость пересекает параллелепипед, параллельны.
Конкретный вид сечения всегда зависит от расположения точек, задающих секущую плоскость.
Куб, все рёбра куба равны, все грани — квадраты
Секущая плоскость может рассекать параллелепипед по-разному, из-за чего сечением может являться 1) треугольник, 2) четырехугольник, 3) пятиугольник, 4) шестиугольник.
Рассмотрим случай, когда сечением параллелепипеда оказывается пятиугольник. При построении сечения руководствуемся правилом, согласно которому отрезки, по которым секущая плоскость пересекает параллелепипед, параллельны.
Конкретный вид сечения всегда зависит от расположения точек, задающих секущую плоскость.
 Рассмотрим случай расположения точек А, B и С на рёбрах параллелепипеда (рис.1). Для построения сечения проводим отрезки AB и ВС. Далее пользуемся вышеуказанным правилом и проводим две прямые: 1) прямую, параллельную ВС, проводим через точку А - в плоскости передней грани параллелепипеда и 2) прямую, параллельную АВ, проводим через точку С - в плоскости боковой грани параллелепипеда. Таким образом, получаем точки Е и D на рёбрах нижней грани параллелепипеда (рис.2). Для завершения построения пятиугольного сечения соединяем точки E и D. Рассмотрим случай расположения точек А, B и С на рёбрах параллелепипеда (рис.1). Для построения сечения проводим отрезки AB и ВС. Далее пользуемся вышеуказанным правилом и проводим две прямые: 1) прямую, параллельную ВС, проводим через точку А - в плоскости передней грани параллелепипеда и 2) прямую, параллельную АВ, проводим через точку С - в плоскости боковой грани параллелепипеда. Таким образом, получаем точки Е и D на рёбрах нижней грани параллелепипеда (рис.2). Для завершения построения пятиугольного сечения соединяем точки E и D.
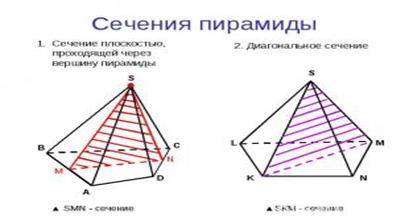
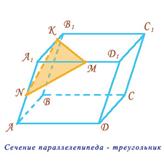 Случай первый (самый простой): сечение – треугольник.
Дан параллелепипед ABCDA1B1C1D1. Точки KMN располагаются на рёбрах A1B1, A1D1 и AA1 соответственно. Строим сечение параллелепипеда плоскостью KMN. Точки M и N одновременно находятся в двух плоскостях: в плоскости AA1D1 и в секущей плоскости. Следовательно, MN – линия пересечения двух указанных плоскостей. Точно так же получаем MK и KN. То есть искомым сечением будет являться треугольник MKN. Случай первый (самый простой): сечение – треугольник.
Дан параллелепипед ABCDA1B1C1D1. Точки KMN располагаются на рёбрах A1B1, A1D1 и AA1 соответственно. Строим сечение параллелепипеда плоскостью KMN. Точки M и N одновременно находятся в двух плоскостях: в плоскости AA1D1 и в секущей плоскости. Следовательно, MN – линия пересечения двух указанных плоскостей. Точно так же получаем MK и KN. То есть искомым сечением будет являться треугольник MKN.
 В стеореометрии есть несколько аналогов теоремы Пифагора. Чаще всего, это теорема о квадрате диагонали прямоугольного параллелепипеда: в прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений. Иногда ---это формула расстояния между двумя точками пространства в прямоугольных координатах. Есть и такой аналог: если боковые ребра тетраэдра попарно перпендикулярны, то квадрат площади основания равен сумме квадратов площадей боковых граней тетраэдра. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. Следствие. Диагонали прямоугольного параллелепипеда равны.
Прямоугольным называется такой параллелепипед, все шесть граней которого являются прямоугольниками. Формула расчета площади его поверхности очень проста: S = 2(ab + bc + ac), где a, b и c – длины ребер.
В стеореометрии есть несколько аналогов теоремы Пифагора. Чаще всего, это теорема о квадрате диагонали прямоугольного параллелепипеда: в прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений. Иногда ---это формула расстояния между двумя точками пространства в прямоугольных координатах. Есть и такой аналог: если боковые ребра тетраэдра попарно перпендикулярны, то квадрат площади основания равен сумме квадратов площадей боковых граней тетраэдра. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. Следствие. Диагонали прямоугольного параллелепипеда равны.
Прямоугольным называется такой параллелепипед, все шесть граней которого являются прямоугольниками. Формула расчета площади его поверхности очень проста: S = 2(ab + bc + ac), где a, b и c – длины ребер.  Билет 14
Логарифмической называется функция вида у = loga x, где а – заданное число, а > 0, а ≠ 1.
Рассмотрим свойства логарифмической функции.
1) Областью определения логарифмической функции является множество всех положительных чисел.
Это утверждение следует из определения логарифма, так как только при х > 0 выражение loga x имеем смысл.
2) Множество значений логарифмической функции представлено множеством R всех действительных чисел.
Это утверждение следует из того, что для любого числа b (b – действительное чсило) есть такое положительное число х, что loga x = b, т.е. уравнение loga x = b имеет корень. Такой корень существует; он равен х = аb, так как loga аb = b.
3) Логарифмическая функция у = loga x является возрастающей на промежутке х > 0, если а > 1, и убывающей, если 0 < а < 1.
Предположим, что а > 1. Докажем, что если х2 > х1 > 0, то у (х2) > у (х1), т.е. loga х2 > loga х1. Пользуясь основным логарифмическим тождеством, условие х2 > х1 можно записать так: а loga х2 >а loga х1. Из этого неравенства по свойству степени с основанием а > 1 следует, что loga х2 > loga х1.
Пусть 0 < а < 1. Докажем, что если х2 > х1 > 0, то loga х2 < loga х1.
Записав условие х2 > х1 в виде а loga х2 > а loga х1, получим loga х2 < loga х1, так как 0 < а < 1.
4) Если а > 1, то при х > 1 функция у = loga x принимает положительные значения, а при при 0 < х < 1 – отрицательные. Если 0 < а < 1, то функция у = loga x принимает положительные значения при 0 < х < 1, отрицательные – при х > 1.
Вопрос 2 билет№2
Билет 15
1.Число е. Функция у = ех, ее свойства, график, дифференцирование
Рассмотрим показательную функцию у=ах, где а > 1. Для различных оснований а получаем различные графики (рис. 232—234), но можно заметить, что все они проходят через точку (0; 1), все они имеют горизонтальную асимптоту у =0 при
Билет 14
Логарифмической называется функция вида у = loga x, где а – заданное число, а > 0, а ≠ 1.
Рассмотрим свойства логарифмической функции.
1) Областью определения логарифмической функции является множество всех положительных чисел.
Это утверждение следует из определения логарифма, так как только при х > 0 выражение loga x имеем смысл.
2) Множество значений логарифмической функции представлено множеством R всех действительных чисел.
Это утверждение следует из того, что для любого числа b (b – действительное чсило) есть такое положительное число х, что loga x = b, т.е. уравнение loga x = b имеет корень. Такой корень существует; он равен х = аb, так как loga аb = b.
3) Логарифмическая функция у = loga x является возрастающей на промежутке х > 0, если а > 1, и убывающей, если 0 < а < 1.
Предположим, что а > 1. Докажем, что если х2 > х1 > 0, то у (х2) > у (х1), т.е. loga х2 > loga х1. Пользуясь основным логарифмическим тождеством, условие х2 > х1 можно записать так: а loga х2 >а loga х1. Из этого неравенства по свойству степени с основанием а > 1 следует, что loga х2 > loga х1.
Пусть 0 < а < 1. Докажем, что если х2 > х1 > 0, то loga х2 < loga х1.
Записав условие х2 > х1 в виде а loga х2 > а loga х1, получим loga х2 < loga х1, так как 0 < а < 1.
4) Если а > 1, то при х > 1 функция у = loga x принимает положительные значения, а при при 0 < х < 1 – отрицательные. Если 0 < а < 1, то функция у = loga x принимает положительные значения при 0 < х < 1, отрицательные – при х > 1.
Вопрос 2 билет№2
Билет 15
1.Число е. Функция у = ех, ее свойства, график, дифференцирование
Рассмотрим показательную функцию у=ах, где а > 1. Для различных оснований а получаем различные графики (рис. 232—234), но можно заметить, что все они проходят через точку (0; 1), все они имеют горизонтальную асимптоту у =0 при 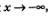 , все они обращены выпуклостью вниз и, наконец, все они имеют касательные во всех своих точках. Проведем для примера касательную к графику функции у=2x в точке х = 0 (рис. 232). Если сделать точные построения и измерения, то можно убедиться в том, что эта касательная образует с осью х угол 35° (примерно). , все они обращены выпуклостью вниз и, наконец, все они имеют касательные во всех своих точках. Проведем для примера касательную к графику функции у=2x в точке х = 0 (рис. 232). Если сделать точные построения и измерения, то можно убедиться в том, что эта касательная образует с осью х угол 35° (примерно). 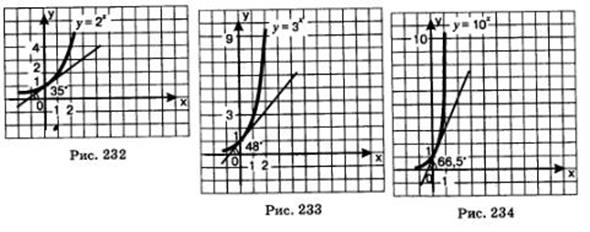 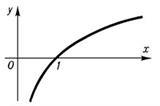
|
e = 2,7182818284590...;
на практике обычно полагают, что e=2,7.
Свойства функции у = ех:
1) 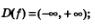
2) не является ни четной, ни нечетной;
3) возрастает;
4) не ограничена сверху, ограничена снизу;
5) не имеет ни наибольшего, ни наименьшего значений;
6) непрерывна;
7) 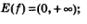
8) выпукла вниз;
9) дифференцируема.
Первообразная показательной функции.
Первообразной для функции аx на R является функция 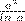 .
.
Действительно, ln a — постоянная, и поэтому
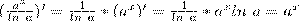
при любом х. Этим доказано, что 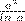 есть первообразная для аx на R. А из равенства (еx)' = еx для всех х следует, что еx есть первообразная для еx на R.
есть первообразная для аx на R. А из равенства (еx)' = еx для всех х следует, что еx есть первообразная для еx на R.
Вопрос 2
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Выпуклый многогранник называется правильным, если его гранями являются равные правильные многоугольники, и в каждой вершине сходится одинаковое число граней.
Рассмотрим возможные правильные многогранники и прежде всего те из них, гранями которых являются правильные треугольники. Наиболее простым таким правильным многогранником является треугольная пирамида, гранями которой являются правильные треугольники (рис. 1,а). В каждой ее вершине сходится по три грани. Имея всего четыре грани, этот многогранник называется также тетраэдром, что в переводе с греческого языка означает четырехгранник.
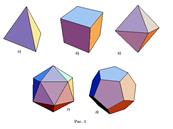
Многогранник, гранями которого являются правильные треугольники, и в каждой вершине сходится четыре грани, изображен на рисунке 1,в. Его поверхность состоит из восьми правильных треугольников, поэтому он называется октаэдром.
Многогранник, в каждой вершине которого сходится пять правильных треугольников, изображен на рисунке 1,г. Его поверхность состоит из двадцати правильных треугольников, поэтому он называется икосаэдром.
Заметим, что поскольку в вершинах выпуклого многогранника не может сходиться более пяти правильных треугольников, то других правильных многогранников, гранями которых являются правильные треугольники, не существует.
Аналогично, поскольку в вершинах выпуклого многогранника может сходиться только три квадрата, то, кроме куба (рис. 1,б), других правильных многогранников, у которых гранями являются квадраты не существует. Куб имеет шесть граней и поэтому называется также гексаэдром.
Многогранник, гранями которого являются правильные пятиугольники, и в каждой вершине сходится три грани, изображен на рисунке 1,д. Его поверхность состоит из двенадцати правильных пятиугольников, поэтому он называется додекаэдром.
| Сумма числа граней и вершин любого многогранника равна числу рёбер, увеличенному на 2. Г + В = Р + 2 Формула Эйлера Число граней плюс число вершин минус число рёбер в любом многограннике равно 2. Г + В Р = 2 |
| Пусть В - число вершин выпуклого многогранника, Р - число его ребер и Г - число граней. Таблица 1 Теорема Эйлера |
| Правильный многогранник Число граней и вершин (Г + В) рёбер (Р) Тетраэдр4 + 4 = 86 Куб6 + 8 = 1412 Октаэдр8 + 6 = 1412 Додекаэдр12 + 20 = 3230 Икосаэдр20 + 12 = 3230 Таблица 2 |
·
| Пусть В - число вершин выпуклого многогранника, Р - число его ребер и Г - число граней. Таблица 1 Число х = В - Р + Г называется эйлеровой характеристикой многогранника. Согласно теореме Эйлера, для выпуклого многогранника эта характеристика равна 2. То, что эйлеровая характеристика равна 2 для многих многогранников, видно из следующей таблицы 2 Тогда верно равенство В - Р + Г = 2 Теорема Эйлера |
| Теорема Эйлера играет огромную роль в математике. С её помощью было доказано огромное количество теорем. Находясь в центре постоянного внимания со стороны математиков, теорема Эйлера получила далеко идущие обобщения. |
·
Билет 16
Двугранный угол. Определение: Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости. Прямая a - ребро, полуплоскости, образующие двугранный угол называют гранями.
Описание слайда:
Признак перпендикулярности двух плоскостей Определение: Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 900.
  Признак перпендикулярности двух плоскостей Теорема: Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.Угол ВАD – линейный угол двугранного угла. Угол ВАD прямой, значит.
Признак перпендикулярности двух плоскостей При решении задач используют следующие утверждения Следствие: Плоскость, перпендикулярная к ребру двугранного угла, перпендикулярна к его граням. Перпендикуляр, проведённый из любой точки одной из двух взаимно перпендикулярных плоскостей к линии их пересечения, есть перпендикуляр к другой плоскости.
Билет17
Показательная функция
Функция вида y = ax, где a больше нуля и а не равно единице называется показательной функцией. Основные свойства показательной функции:
1. Областью определения показательной функции будет являться множество вещественных чисел.
2. Область значений показательной функции будет являться множество всех положительных вещественных чисел. Иногда это множество для краткости записи обозначают как R+.
3. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0<a
4. Справедливы будет все основные свойства степеней. Основные свойства степеней представлены следующим равенствами:
ax*ay = a(x + y);
(ax)/(ay) = a(x-y);
(a*b)x = (ax)*(ay);
(a/b)x = ax/bx;
(ax)y = a(x * y).
Данные равенства будут справедливы для все действительных значений х и у.
5. График показательной функции всегда проходит через точку с координатами (0;1)
6. В зависимости от того возрастает или убывает показательная функция, её график будет иметь один из двух видов.
На следующем рисунке представлен график возрастающей показательной функции: a>0. Признак перпендикулярности двух плоскостей Теорема: Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.Угол ВАD – линейный угол двугранного угла. Угол ВАD прямой, значит.
Признак перпендикулярности двух плоскостей При решении задач используют следующие утверждения Следствие: Плоскость, перпендикулярная к ребру двугранного угла, перпендикулярна к его граням. Перпендикуляр, проведённый из любой точки одной из двух взаимно перпендикулярных плоскостей к линии их пересечения, есть перпендикуляр к другой плоскости.
Билет17
Показательная функция
Функция вида y = ax, где a больше нуля и а не равно единице называется показательной функцией. Основные свойства показательной функции:
1. Областью определения показательной функции будет являться множество вещественных чисел.
2. Область значений показательной функции будет являться множество всех положительных вещественных чисел. Иногда это множество для краткости записи обозначают как R+.
3. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0<a
4. Справедливы будет все основные свойства степеней. Основные свойства степеней представлены следующим равенствами:
ax*ay = a(x + y);
(ax)/(ay) = a(x-y);
(a*b)x = (ax)*(ay);
(a/b)x = ax/bx;
(ax)y = a(x * y).
Данные равенства будут справедливы для все действительных значений х и у.
5. График показательной функции всегда проходит через точку с координатами (0;1)
6. В зависимости от того возрастает или убывает показательная функция, её график будет иметь один из двух видов.
На следующем рисунке представлен график возрастающей показательной функции: a>0.
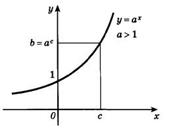 На следующем рисунке представлен график убывающей показательной функции: 0<a<1.
На следующем рисунке представлен график убывающей показательной функции: 0<a<1.
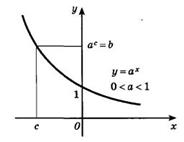 И график возрастающей показательной функции и график убывающей показательной функции согласно свойству, описанному в пятом пункте, проходят через точку (0;1).
7. Показательная функция не имеет точек экстремума, то есть другими словами, она не имеет точек минимума и максимума функции. Если рассматривать функцию на каком-либо конкретном отрезке, то минимальное и максимальное значения функция будет принимать на концах этого промежутка.
8. Функция не является четной или нечетной. Показательная функция это функция общего вида. Это видно и из графиков, ни один из них не симметричен ни относительно оси Оу, ни относительно начала координат.
Вопрос 2. Билет 5
Билет 18
Решение показательных уравнений
Показательными называются уравнения, в которых неизвестная переменная находится только в показателях каких-либо степеней.
Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему:
Теорема 1. Показательное уравнение af (x) = ag (x) (где a > 0, a ≠ 1) равносильно уравнению f (x) = g (x).
Помимо этого, полезно помнить об основных формулах и действиях со степенями:
И график возрастающей показательной функции и график убывающей показательной функции согласно свойству, описанному в пятом пункте, проходят через точку (0;1).
7. Показательная функция не имеет точек экстремума, то есть другими словами, она не имеет точек минимума и максимума функции. Если рассматривать функцию на каком-либо конкретном отрезке, то минимальное и максимальное значения функция будет принимать на концах этого промежутка.
8. Функция не является четной или нечетной. Показательная функция это функция общего вида. Это видно и из графиков, ни один из них не симметричен ни относительно оси Оу, ни относительно начала координат.
Вопрос 2. Билет 5
Билет 18
Решение показательных уравнений
Показательными называются уравнения, в которых неизвестная переменная находится только в показателях каких-либо степеней.
Для решения показательных уравнений требуется знать и уметь использовать следующую несложную теорему:
Теорема 1. Показательное уравнение af (x) = ag (x) (где a > 0, a ≠ 1) равносильно уравнению f (x) = g (x).
Помимо этого, полезно помнить об основных формулах и действиях со степенями:
 Пример 1. Решите уравнение:
Пример 1. Решите уравнение:
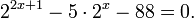 Решение: используем приведенные выше формулы и подстановку:
Решение: используем приведенные выше формулы и подстановку:
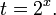 Уравнение тогда принимает вид:
Уравнение тогда принимает вид:
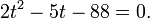 Дискриминант полученного квадратного уравнения положителен:
Дискриминант полученного квадратного уравнения положителен:
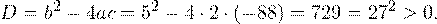 Это означает, что данное уравнение имеет два корня. Находим их:
Это означает, что данное уравнение имеет два корня. Находим их:
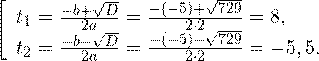 Переходя к обратной подстановке, получаем:
Переходя к обратной подстановке, получаем:
 Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе:
Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе:
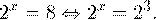 С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию.
Ответ: x = 3.
Вопрос 2 билет 13
Билет 19.
Перейти к списку задач и тестов по теме "Логарифмы. Свойства логарифмов"
Определение: Логарифмом положительного числа b по основанию
С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию.
Ответ: x = 3.
Вопрос 2 билет 13
Билет 19.
Перейти к списку задач и тестов по теме "Логарифмы. Свойства логарифмов"
Определение: Логарифмом положительного числа b по основанию 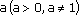 называется показатель степени с, в которую надо возвести число а, чтобы получить число b. называется показатель степени с, в которую надо возвести число а, чтобы получить число b.
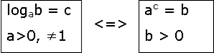 Основное логарифмическое тождество:
Основное логарифмическое тождество:
 Свойства логарифмов:
Свойства логарифмов:
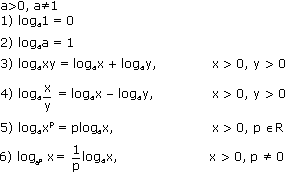 7) Формула перехода к новому основанию:
7) Формула перехода к новому основанию:
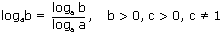 Десятичный логарифм:
lg a = log10a
Натуральный логарифм:
lna = logea, e ≈ 2,718…
вопрос 2
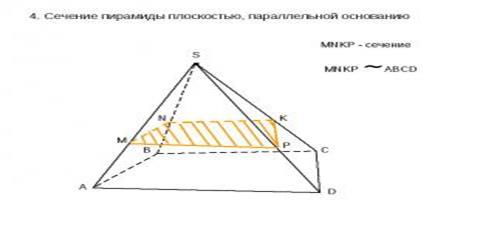
Пирами́да (др.-греч. πυραμίς, род. п. πυραμίδος) — многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину[1]. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д. Пирамида является частным случаем конуса[2].
Правильная пирамида[
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:
боковые рёбра правильной пирамиды равны;
в правильной пирамиде все боковые грани — конгруэнтные равнобедренные треугольники;
в любую правильную пирамиду можно как вписать, так и описать вокруг неё сферу;
если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна
Десятичный логарифм:
lg a = log10a
Натуральный логарифм:
lna = logea, e ≈ 2,718…
вопрос 2
Пирами́да (др.-греч. πυραμίς, род. п. πυραμίδος) — многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину[1]. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д. Пирамида является частным случаем конуса[2].
Правильная пирамида[
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:
боковые рёбра правильной пирамиды равны;
в правильной пирамиде все боковые грани — конгруэнтные равнобедренные треугольники;
в любую правильную пирамиду можно как вписать, так и описать вокруг неё сферу;
если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна 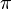 , а каждый из них соответственно , а каждый из них соответственно 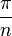 , где n — количество сторон многоугольника основания[8];
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Прямоугольная пирамида[
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.
Тетраэдр[править |
Тетраэдром называется треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды. Кроме того, существует большое различие между понятиями «правильная треугольная пирамида» и «правильный тетраэдр». Правильная треугольная пирамида — это пирамида с правильным треугольником в основании (грани же должны быть равнобедренными треугольниками). Правильным тетраэдром является тетраэдр, у которого все грани являются равносторонними треугольниками. , где n — количество сторон многоугольника основания[8];
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Прямоугольная пирамида[
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.
Тетраэдр[править |
Тетраэдром называется треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды. Кроме того, существует большое различие между понятиями «правильная треугольная пирамида» и «правильный тетраэдр». Правильная треугольная пирамида — это пирамида с правильным треугольником в основании (грани же должны быть равнобедренными треугольниками). Правильным тетраэдром является тетраэдр, у которого все грани являются равносторонними треугольниками.

|
Билет 20
Функция F, заданная на некотором промежутке D, называется первообразной функции f, заданной на том же промежутке, если для любого 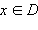
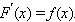
|
Так, функция 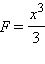 является первообразной функции
является первообразной функции  в чем можно убедиться, поставив эти функции в определение первообразной. Функция
в чем можно убедиться, поставив эти функции в определение первообразной. Функция 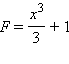 также является первообразной функции
также является первообразной функции 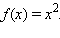
Если функция F является первообразной функции f, то все функции вида F + C, где C – константа, и только они являются первообразными функции f.
Таким образом, для любой функции ее первообразная F определяется неоднозначно. Для того, чтобы задать ее однозначно, нужно указать точку A (x 0; y 0), удовлетворяющую уравнению y = F (x).

Вопрос 2
Параллельность плоскостей
Две плоскости параллельны, если они не имеют общих точек.
Это определение. Однако в практических целях чаще используется признак параллельности плоскостей:
Плоскости параллельны друг другу, если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.
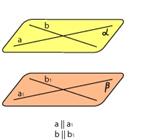
Свойства параллельных плоскостей:
Если две плоскости параллельны третьей, то они параллельны друг другу.
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны. 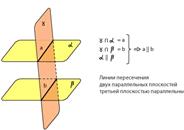
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
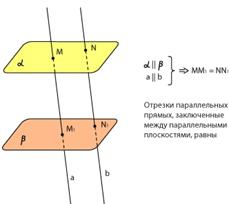
Билет 21
Функция- зависимость переменной у от переменной x
, если каждому значению х соответствует единственное значение у.
Переменная х- независимая переменная или аргумент.
Переменная у- зависимая переменная
Значение функции- значение у, соответствующее заданному значению х.
Область определения функции- все значения, которые принимает независимая переменная.
Область значений функции (множество значений)- все значения, которые принимает функция.
Функция является четной- если для любого х из области определения функции выполняется равенство f(x)=f(-x)
Функция является нечетной- если для любого х из области определения функции выполняется равенство f(-x)=-f(x)
Возрастающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)<f(х2)
Убывающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2)
Способы задания функции.
Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x)- с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.
Date: 2015-07-24; view: 1013; Нарушение авторских прав