Определение производной

Производной функции в точке х₀ называется предел отношения 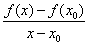приращения функции к вызвавшему его приращению аргумента при стремлении х к х₀. Производная функции в точке х₀ обозначается символом .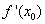

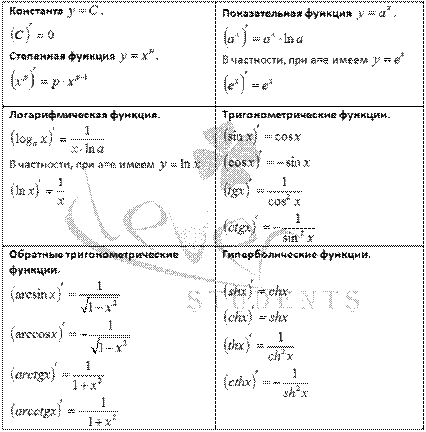
Правила вычисления производных

Пусть c -положительное число u=u(x), v=v(x) и кроме этого у этих функции существуют производные.

Тогда справедливы следующие формулы:

1). c ´=0

2). (c · u(x))´= c · u ´ (x)

3). (u(x) 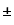v(x))´= u ´ (x) 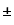v ´ (x)

4). (u(x)· v(x))´= u ´ (x)·v(x) + u(x)·v ´ (x)

5). ()´=

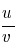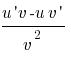
Вопрос2

Конусом (точнее, круговым конусом) называется тело, кото­рое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга,— вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания (рис. 1). Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса. Поверхность конуса состоит из основания и боковой поверхности.

рисунок 4 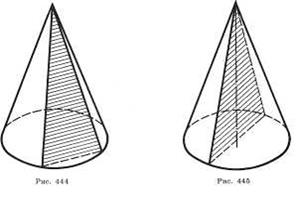рисунок 5 рисунок 6

Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 3). В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса (рис. 4). Теорема. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность - по окружности с центром на оси конуса. Доказательство. Пусть 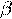- плоскость, параллельная плоскости основания конуса и пересекающая конус (рис.5). Преобразование гомотетии относительно вершины конуса, совмещающее плоскость 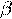с плоскостью основания, совмещает сечение конуса плоскостью 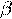с основанием конуса. Следовательно, сечение конуса плоскостью есть круг, а сечение боковой поверхности – окружность с центром на оси конуса. Теорема доказана.

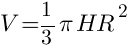
Билет 25

Определение первообразной.

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство 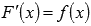для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство 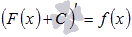. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Определение неопределенного интеграла.

Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .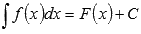

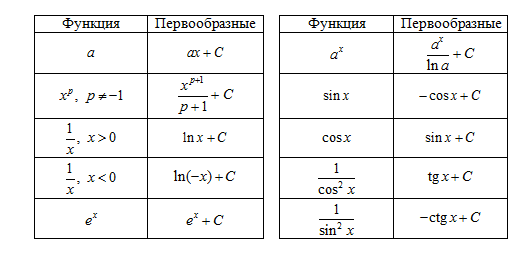
Три правила нахождения первообразных.
Правило 1. Если F есть первообразная для f, а G - первообразная для g, то F+G 0есть первообразная для f+g.

3(F+G)'=F'+G'=f+g

Правило 2. Если F есть первообразная для f, а k - постоянная то функция kF - первообразная для kf.

3(kF)'=kF'=kf

Правило 3. Если F(x) есть первообразная для f(x), а k и b - постоянные, причем 2 k 7- 20 0, то 2 1/k*F(kx+b) 0 есть первообразная для f(kx+b).

3(1/k*F(kx+b))'=1/k*F'(kx+b)*k=f(kx+b).

Вопрос 2 билет№3

Билет 26

Криволине́йная трапе́ция — плоская фигура, ограниченная графиком неотрицательной непрерывной функции 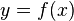, определенной на отрезке [a; b], осью абсцисс и прямыми и 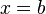.Для вычисления площадей криволинейных трапеций применяется следующая теорема:

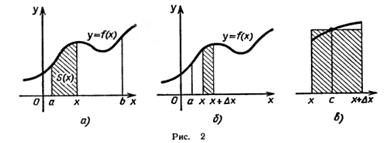
Теорема. Если f — непрерывная и неотрицательная на отрезке [а; b] функция, a F — ее первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции (рис. 2) равна приращению первообразной на отрезке [а; b] т. е.

S=F(b)-F(a). (1)

Доказательство. Рассмотрим функцию S (х), определенную на отрезке [а; b]. Если а <x≤b, то S (х) — площадь той части криволинейной трапеции, которая расположена левее вертикальной прямой, проходящей через точку М (х; 0) (рис. 2, а). Если х=а, то S (а) = 0. Отметим, что S(b)=S (S — площадь криволинейной трапеции).

Взаимное расположение прямой и плоскости в пространстве.

Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.

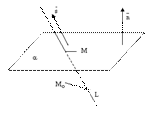
Теорема. Пусть плоскость задана общим уравнением

,

а прямая L задана каноническими уравнениями

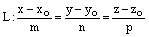
или параметрическими уравнениями

, ,

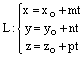в которых 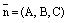– координаты нормального вектора плоскости , – координаты произвольной фиксированной точки прямой L, –

координаты направляющего вектора прямой L. Тогда:

1) если 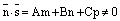, то прямая L пересекает плоскость в точке, координаты которой 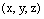можно найти из системы уравнений

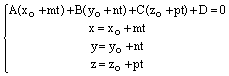; (7)

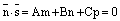2) если и 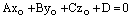, то прямая лежит на плоскости;

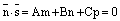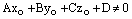3) если и , то прямая параллельна плоскости.

Продполжение в билете 25-признак параллельности или в билете №3

Билет 27

Date: 2015-07-24; view: 560; Нарушение авторских прав