Билет 5

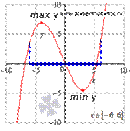
Необходимое условие экстремума: Если точка х является точкой экстремума функции f и в этой точке существует производная f ′, то она равна нулю: f′(х°) =0.

Признак максимума функции: Если функция f непрерывна в точке х, а f ′ (х)> 0 на интервале (а;х°) и f ′ (х)< 0 на интервале (х°; в), то точка х является точкой максимума функции f.

Признак минимума функции: Если функция f непрерывна в точке х°, а f ′ (х)< 0 на интервале (а;х°) и f ′ (х)> 0 на интервале (х°; в), то точка х° является точкой максимума функции f.

Исследование функции:

1. Найти область определения функции

2. Выяснить, является ли функция четной или нечетной, является ли периодической.

3. Найти точки пересичения с осями координат

4. Найти промежутки знакопостоянства

5. Найти промежутки воз и убыв.

6. Точки эстремума и значения функции в этих точках

7. Построить график

Определение. Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником. Основными элементами многогранника являются грани, ребра, вершины.

Грани – это многоугольники, составляющие многогранник.

Ребра – это стороны граней.

Вершины – это концы ребер.

Виды призм:

Треугольная призма

То есть АВСА₁В₁С₁ – треугольная призма, если:

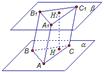1) Треугольники АВС и А₁В₁С₁ равны.

2) Треугольники АВС и А₁В₁С₁ расположены в параллельных плоскостях α и β: ABC ║ А₁B₁C (α ║ β).

3) Ребра АА₁, ВВ₁, СС₁ параллельны

Прямая призма

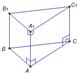Эта призма – прямая. То есть, ее боковые ребра перпендикулярны основаниям.

Наклонная призма

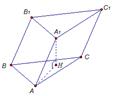Здесь боковое ребро не перпендикулярно плоскости основания. Если опустить из точки А₁ перпендикуляр А₁Н на АВС, то этот перпендикуляр будет высотой призмы. Заметим, что отрезок АН – это проекция отрезка АА₁ на плоскость АВС.

Четырехугольная призма

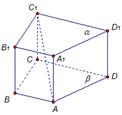1) Четырехугольник ABCD равен четырехугольнику A₁B₁C₁D₁: ABCD = A₁B₁C₁D₁.

2) Четырехугольники ABCD и A₁B₁C₁D₁ лежат в параллельных плоскостях α и β: ABC ║ А₁B₁C (α ║ β).

3) Четырехугольники ABCD и A₁B₁C₁D₁ расположены так, что боковые ребра параллельны, то есть: АА₁║ВВ₁║СС₁║DD₁.

Паралилепипед

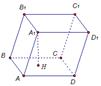Частным случаем четырёхугольной призмы является известный нам параллелепипед. Параллелепипед ABCDA₁B₁C₁D₁ изображен на рис. 7.

Шестиугольная призма. В основании шестиугольник, все стороны параллельны.

Правильная призма. Определение. Прямая призма называется правильной, если её основания – правильные многоугольники.

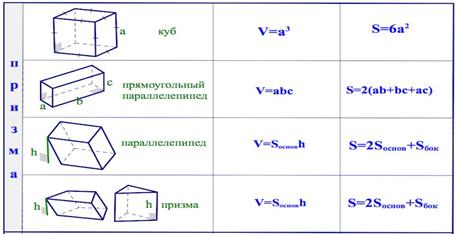
Билет 6

Наибольшим значением функции y=f(x) на промежутке X называют такое значение, что для любого справедливо неравенство.

Наименьшим значением функции y=f(x) на промежутке X называют такое значение, что для любого справедлив0 неравенство.

Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе.

Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.

1.Находим область определения функции и проверяем, содержится ли в ней весь отрезок [a;b].

2. Находим все точки, в которых не существует первая производная и которые содержатся в отрезке [a;b] (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.

3. Определяем все стационарные точки, попадающие в отрезок [a;b]. Для этого, находим производную функции, приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни. Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту.

4…Вычисляем значения функции в отобранных стационарных точках (если такие имеются), в точках, в которых не существует первая производная (если такие имеются), а также при x=a и x=b.

5..Из полученных значений функции выбираем наибольшее и наименьшее - они и будут искомыми наибольшим и наименьшим значениями функции соответственно.

Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.

Конец отрезка, лежащий в плоскости, называется основанием наклонной.

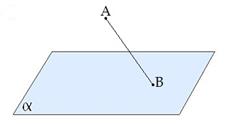
AB - наклонная.
B - основание наклонной.

Перпендикуляром, проведенным из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости.

Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.

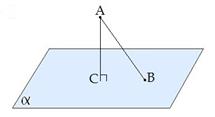
AC - перпендикуляр.

C - основание перпендикуляра.

Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к плоскости.

Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.

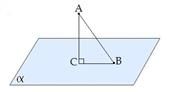
CB - проекция наклонной AB на плоскость α.

Треугольник ABC прямоугольный.

Углом между наклонной и плоскостью называется угол между этой наклонной и её проекцией на плоскость.

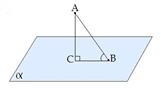
∢CBA - угол между наклонной AB и плоскостью α.

Date: 2015-07-24; view: 1147; Нарушение авторских прав