Бірқалыпты жинақты функционалды қатарлардың қасиеттері

1 º. Функционалды қатар қосындысының үзіліссіздігі. 11.16 Теорема. Егер бірқалыпты мақсаты 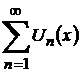функционалды қатардың әрбір мүшесі 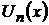функциялары 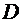аймағында үзіліссіз болса, онда қатардың қосындысы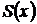 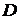аймағында үзіліссіз болады.

2 º. Функционалды қатарды мүшелеп интегралдау. 11.17 Теорема. Егер әрбір мүшесі берілген аралықта үзіліссіз болатын 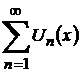функционалды қатарын өзінің 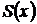қосындысына 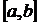кесіндісінде бірқалыпты жинақты болса, онда ол қатарды 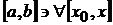кесіндісінде мүшелеп интегралдауға болады, яғни

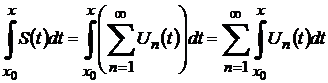, (11.26)

теңдігі орындалады.

3 º. Функционалды қатарды мүшелеп дифференциалдау. 11.18 Теорема. Айталық, әрбір мүшесі үзіліссіз дифференциалданатын 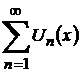қатары 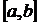кесіндісінде 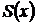функциясына жинақты, ал 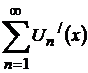қатары берілген кесіндісінде бірқалыпты жинақты болсын. Онда берілген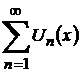 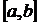кесіндісінде бірқалыпты жинақты, ал оның қосындысы 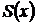үзіліссіз дифференциалданатын функция және

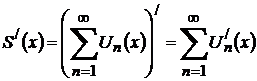(11.27)

теңдігі орындалады.

М.16*. 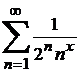, қатарының 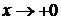-дағы шегін табайық.

Шешуі. Вейерштарсс белгісі бойынша, берілген функционалды қатардың мажорантты, 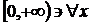үшін 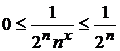болады. Демек, берілген қатар бірқалыпты жинақты. Онда 11.16 Теоремадан туатын салдар бойынша, қатарда мүшелеп шекке көшуге болады, яғни

.

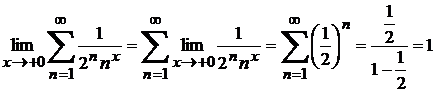М.17*. 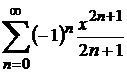, қатардың қосындысын есептейік.

Шешуі. Берілген қатардың туындысынан тұратын,

(*)

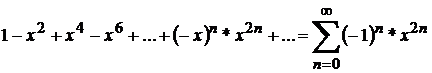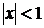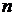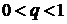қатарын қарастырайық. Мұндағы болғанда, (*) қатардың -дербес қосынды, кемімелі геометриялық прогрессия. Онда оның қосындысы, . Енді (*) қатардың болғанда 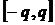кесіндісінде бірқалыпты жинақты болатындығына көз жеткізейік. Шынында да, 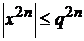болғандықтан, (*) функционалды қатар үшін 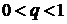болғанда 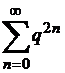сандық қатары мажорант болады. Демек, (*) қатар бірқалыпты жинақты. Ендеше, (*) қатарды 11.17 теорема бойынша мүшелеп интегралдауға болады, яғни

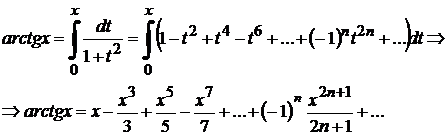
Мұндағы .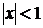

М.18*. 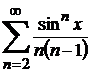, қатарының қосындысын табайық.

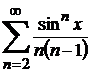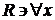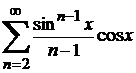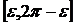
Шешуі. Берілген қатардың мажоранты ─ сандық қатары болғандықтан үшін ол қатар бірқалыпты жинақты. Ал ол қатардан алынған туынды қатар ─ 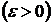кесіндісінде бірқалыпты жинақты. Онда ,

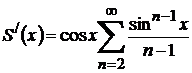
және , .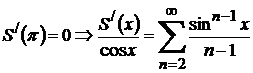

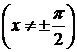Бұл теңдікті дифференциалдау арқылы, 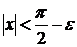болғанда 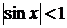болатындығын ескере отырып,

(*)

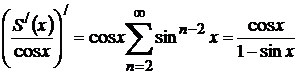теңдігін аламыз. Мұндағы 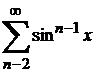қатарының бірқалыпты жинақты болатындығын М.17*- қатар сияқты көрсетуге болады. Енді (*) теңдікті интегралдасақ:

.

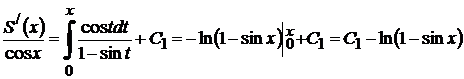Өз кезегінде, 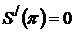болғандықтан 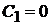. Ендеше, (**) теңдіктен, 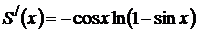. Енді екінші рет интегралдау арқылы,

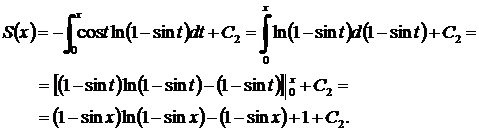
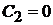Ал болғандықтан, , Сонымен, , , .

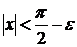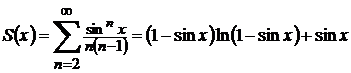Date: 2015-07-23; view: 2217; Нарушение авторских прав