Таңбалары әртүрлі сандық қатарлар

1. Абсолютті және шартты жинақтылық. Айталық, 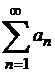сандық қатар болсын. Осы қатар сәйкес, 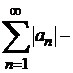мүшелері берілген қатардың тек абсолют шамаларынан тұратын жаңа қатар құрайық. Егер: жаңа 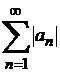қатар жинақты болса, онда берілген 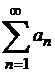қатар абсолютті жинақты, ал жаңа қатар жинақсыз, берілген қатардың өзі жинақты болса, онда ол шартты жинақты деп аталады.

М, 10*, а) 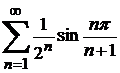, ә)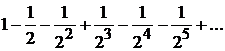

қатарларын жинақтылыққа зерттейік.

Шешуі. Берілген қатарлардың мүшелерінің абсолютті шамаларынан құралған 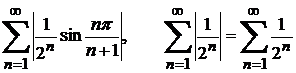қатарларды қарастырамыз. Олардың біріншісінен, 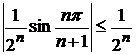болатындығы белгілі. Ендеше, 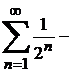мүшелері кемімелі геометриялық прогрессия болатын қатар. Ондай қатар жинақты. Ендеше, берілген екі қатар да абсолютті жинақты.

2. Таңбалары алма-кезек ауысатын қатарлар. 11.10 Теорема ( Лейбниц белгісі ). Айталық, таңбалары алма-кезек ауысатын (11.11) қатары берілген болсын. Анығырақ болу үшін 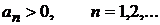болсын. Егер: біріншіден,

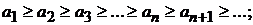
екіншіден, болса, онда берілген қатар жинақты, ал қатардың қосындысы бірінші мүшеден аспайды және қалдық қатар үшін 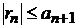ара қатынасы орындалады.

Мұндай шарттарды қанағаттындыратын қатарлар Лейбниц қатарлары деп аталады.

Мысал үшін, 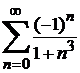- Лейбниц қатары болғандықтан жинақты, ал оның қосындысын ге дейінгі дәлдікпен табатын болсақ,

.

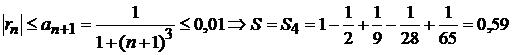Date: 2015-07-23; view: 2368; Нарушение авторских прав