Сандық қатар және оның қосындысы

Сандық қатарлар

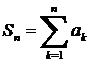─ сандық қатардың n- дербес қосындысы деп аталады.

Егер

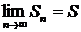(11.2)

бар және ақырлы болса, онда сандық қатар жинақты, ал (11.2) шек жоқ немесе шектелмеген болса, қатар жинақсыз деп аталады. Берілген (11.1) қатардың шегі болатын S саны оның қосындысы деп аталады.

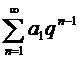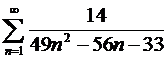М.1*. а) ; ә) ; б) 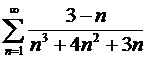; қатарларын жинақтылыққа зерттеп, егер жинақты болса олардың қосындысын табайық.

Шешу. а) Берілген қатардың мүшелері - 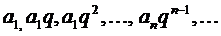еселігі 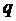болатын, геометриялық прогресия болып табылады. Ендеше, оның алғашқы 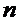-мүшесінің қосындысы,

(*)

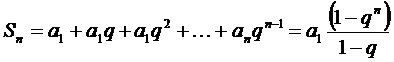
өрнегімен анықталады. Бұдан 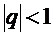болғанда 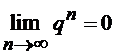, ал 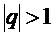- 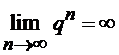болатындығын көреміз. Еендеше, (*) n -дербес қосындыдан шекке көшсек, 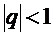болғанда қатардың қосындысы

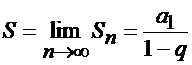
болып шығады. Демек, қатар жинақты.

Егер де, 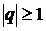болса, берілген қатар жинақсыз.

ә) Берілген сандық қатардың бөлімін түрлендіру арқылы, жәй бөлшектерге жіктейік. Сондықтан,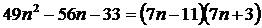

болғандықтан 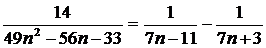. (1)

Онда (1) жәй бөлшекті пайдаланып берілген сандық қатардың n -дербес мүшесін мына түрде жазуға болады:

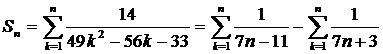(2)

Енді бұл қосындыны жеке-жеке ашып жазайық,

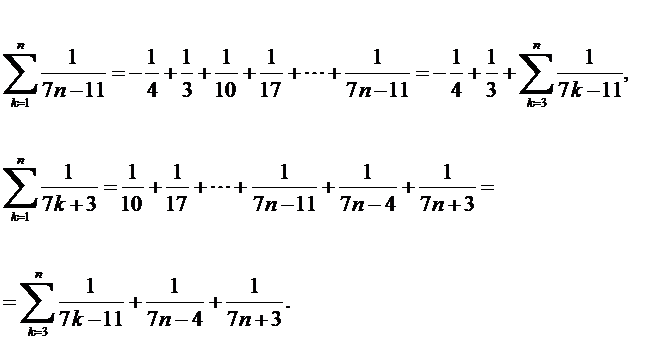
Онда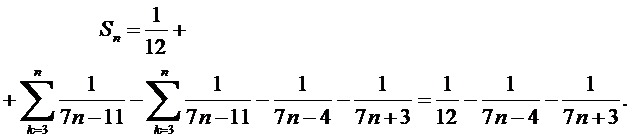

Демек, (11.2) шекті тапсақ

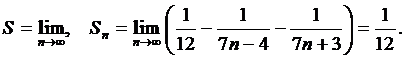
Ендеше, берілген сандық қатар жинақты, ал оның қосындысы .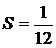

б) Жаңағы тәсіл бойынша қатар астындағы өрнекті жәй бөлшектерге жіктейік

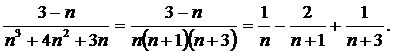
Онда

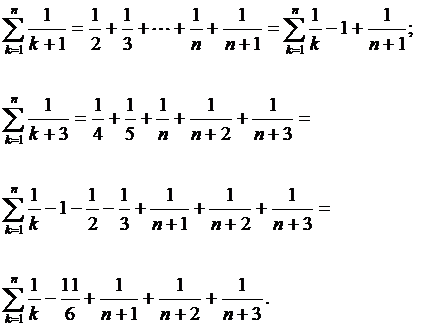
Енді берілген қатарға сәйкес n -дербес қосындыны құрайық, яғни

Ендеше,

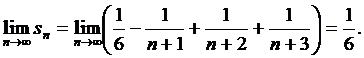
Бұдан берілген қатар жинақты, ал оның қосындысы 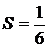болсын.

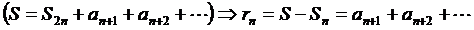(11.3)

қалдық қатар деп аталады.

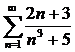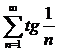М. 4*. а) , ә) қатарларын жинақтылыққа зерттейік.

Шешуі. а) Бірінші қатардан

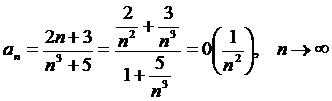
Болғандықтан, оны 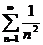бигармоникалық жинақты қатармен (М, 3*) салыстырайық. Онда (11.7) қатынасты қарастыралық

.

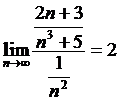Ендеше, 11.5 теорема бойынша берілген а) қатары жинақты.

ә) Бұл қатарды 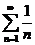гармоникалық жинақсыз қатармен (М. 3*) салыстырайық, 11.5-шектік теорема бойынша, 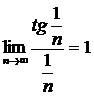. Демек, берілген қатар жинақсыз.

11.6 Теорема (Д’Аламбер белгісі). Айталық, 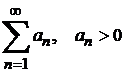қатары үшін

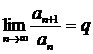(11.8)

шегі бар болсын. Онда:

1º. 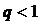- берілген қатар жинақты;

2º, 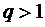- қатар жинақсыз.

11.7 Теорема (Коши белгісі). Айталық, 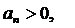болғандағы 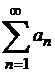сандық қатары үшін

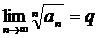(11.9)

шегі бар болсын. Онда:

1º. 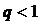- қатар жинақты;

2º. 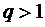- қатар жинақсыз.

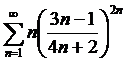М.5*. а) ; ә) қатарларын жинақтылыққа зерттейік.

Шешуі. Д’аламбер белгісі бойынша тексерейік,

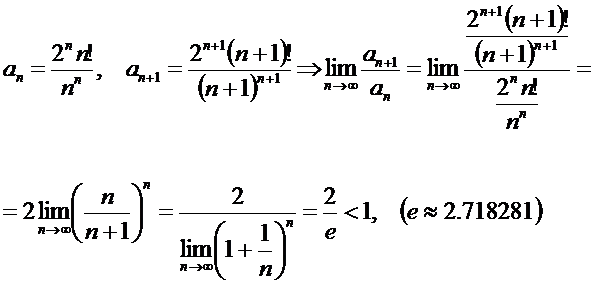
Демек, берілген қатар жинақты.

ә) Коши белгісін пайдаланайық,

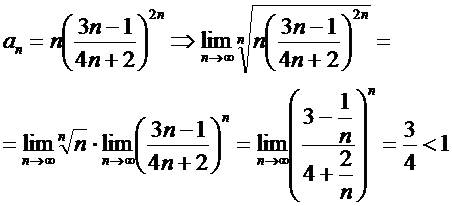
Ендеше, берілген қатар жинақты.

Ескерту. Егер 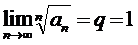, 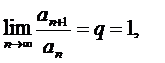болғанда, зерттелетін қатар жинақты да, жинақсыз да болуы мүмкін. Мысал үшін, гармоникалық және бигармоникалық қатарлар үшін:

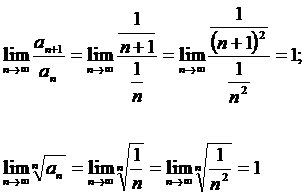
Ал, 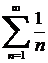─ гармоникалық қатардың жинақсыз. 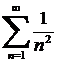─ бигармоникалық қатардың жинақты болатындығы, жоғары да 3*-мысалда көрсетілген.

11.8 Теорема (Коши теоремасы). Мүшелер 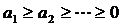ара қатынаста болатын 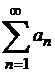қатарының жинақты болуы,

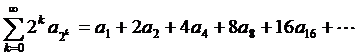
қатарының жинақты болуымен тікелей байланысты.

М.6*. 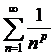─ Дирихле қатарын жинақтылыққа зерттейік.

Шешуі. Егер болады да, қатар жинақтылының қажетті шарты орындалмайды. Демек, 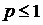болғанда Дирихле қатары жинақсыз.

Айталық, 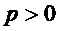болсын. Енді көмекші

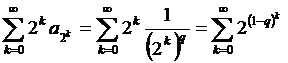
қатарын қарастырайық, Егер 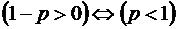болса, (*) қатары, еселігі 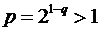болатын геометриялық прогрессияның қосындысы болғандықтан, жинақсыз болады. Ал 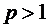болғанда (*) қатары 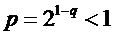болғандықтан, жинақты.

Сонымен, соңғы 11.8 Коши теоремасы бойынша, 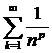─ Дирихле қатары 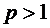болғанда жинақты және 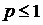болғанда жинақсыз болады.

М.7*. 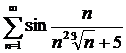қатарын жинақтылыққа зерттейік.

Шешуі. Берілген қатарды 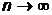-дықтан, мүшелері

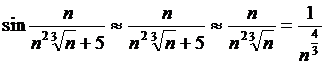
болатын қатармен салыстырудың шектік белгісімен (11.5 Т.) салыстырамыз, яғни

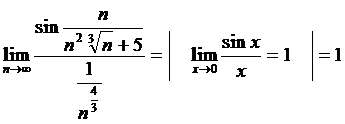
Демек, 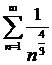─ Дирихле қатары 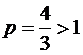болғандықтан жинақты. Ендеше, берілген қатар жинақты.

11.9 Теорема (Коши-Маклореннің интегралдық белгісі). Айталық, 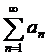қатарының барлық мүшесін (көңілде ғана - (формально)) 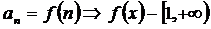аралығында теріс болмайтын монотонды функция ретінде қарастырайық. Онда берілген 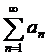қатарының жинақты (я жинақсыз) болуы, 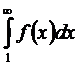меншіксіз интегралының жинақты (я жинақсыз) болуымен тікелей байланысты болады.

М.8*. 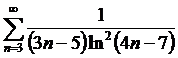қатарын жинақтылыққа зерттейік.

Шешуі. Келтірілген Коши-Маклореннің интегралдық белгісін бірден қолдансақ, 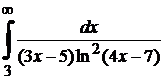меншіксіз интегралын жинақтылыққа зерттеуіміз қажет. Бірақ ол ауырлыққа келтіретін болғандықта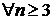н, үшін

(*)

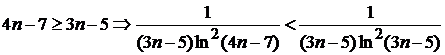Енді берілген қатарды одан үлкенірек болатын 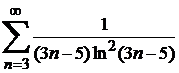қатарымен салыстырамыз. Бұған Коши-Маклореннің интегралдық белгісін қолдану жеңіл. Сонымен,

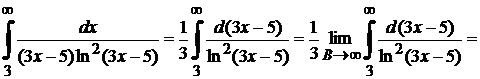
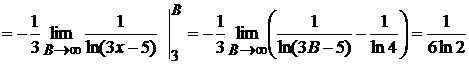
Демек, меншіксіз интеграл жинақты. Онда оған сәйкес 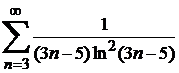қатары жинақты. Өз кезегінде, (*) ара қатынасты еске алсақ, жинақтылықтың салыстыру белгісі бойынша, берілген қатардың жинақтылықтылығы шығады.

М.9*. 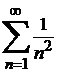қатарының қосындысын 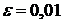-ге дейінгі дәлдікпен табайық.

Шешуі. 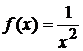болғандықтан, берілген қатарға сәйкес қалдық қатар үшін алынған (11.10) бағаны ескеру арқылы:

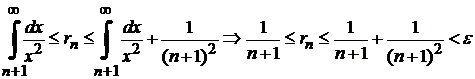
Бұдан 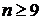екендігі шығады. Ендеше,

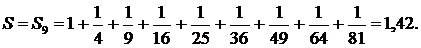
Date: 2015-07-23; view: 11188; Нарушение авторских прав