Таңбалары әртүрлі жинақты қатарлар қасиеттері

М. 11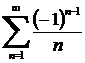^*. , қатарын қарастырайық.

Шешуі. Біріншіден, бұл қатар Лейбниц қатары болғандықтан жинақты. Екіншіден, 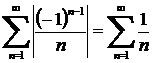- гармоникалық қатар жинақсыз. Ендеше, қарастырылып отырған қатар шартты жинақты.

Айталық, 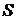берілген қатардың қосындысы болсын.

Онда , Енді берілген қатар мүшелерін – екі оң мүшеден кейін бір теріс сан келетіндей етіп қосылғыштардың орындарын ауыстырайық,

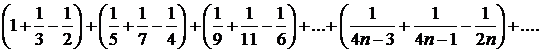
Мұндағы 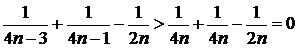болғандықтан, 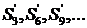дербес қосындылар тізбегі үшін 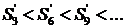ара қатынастары орындалады, яғни (*) қатардың қосындысы болса, онда 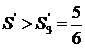, Ал шын мәнінде 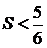. Қарама-қайшылық: 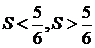пайда болды. Демек, берілген жинақты қатардың орындарын ауыстырғаннан оның қосындысының өзгермейтіндігінен байқадық. Сондықтан, осы мәселеге тоқталғанымыз жөн болатын сияқты.

5º. 11.11 Теорема ( Дирихле ). Егер 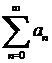қатары абсолютті жинақты және қосындысы 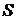болса, онда осы қатар мүшелерінің ауыстырғаннан қатардың жинақтылығы және қосындысы өзгермейді, яғни қатар абсолютті жинақты және қосындысы 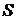болады.

6º, 9, 12 Теорема ( Риман теоремасы ), Егер 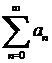қатары шартты жинақты болса, онда кез келген алдын ала алған 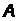саны үшін, қосындысы осы 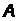санына тең болатындай етіп берілген қатар мүшелерінің орындарын ауыстыруға болады

Date: 2015-07-23; view: 1896; Нарушение авторских прав