Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Метод окаймляющих миноров
|
|
Алгоритм в общем виде, боюсь, будет мало кому понятен, гораздо проще разобрать его на конкретной задаче:
Пример 1
Найти ранг матрицы методом окаймляющих миноров
Решение: дана квадратная матрицы «четыре на четыре» и, очевидно, её ранг не превосходит 4-х.
Заряжаем:
Поскольку есть ненулевые элементы, следовательно, ранг не менее единицы.
Проверку миноров 2-го порядка начинаем с так называемого углового минора 
.
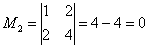, поэтому переходим к минору 
:
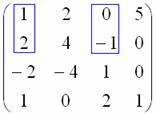, значит, ранг матрицы не менее двух. Что было бы нужно сделать, если бы и этот минор оказался нулевым? В этом случае рассматриваем минор 
, и если он тоже равен нулю, едем дальше:
, 
, 
.
При необходимости (когда получились одни нули), следует продолжить перебор миноров по аналогичной схеме у:
1-ой и 3-ей строк;
1-ой и 4-ой строк;
2-ой и 4-ой строк;
3-ей и 4-ой строк – до тех пор, пока не повстречается минор, отличный от нуля.
Если все миноры 2-го порядка оказались нулевыми, то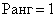 
.
Но в нашем случае уже на втором шаге обнаружен «хороший» минор, и теперь мы переходим к рассмотрению миноров третьего порядка. Приделываем ноги младшему коллеге 
, который будет входить во все рассматриваемые миноры высших порядков:
Вопрос «третьим будешь?» может быть адресован либо красному, либо зелёному товарищу:
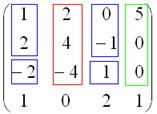
Был бы пятый столбец – нашёлся бы ещё один друг.
Начнём с красного:
Не помогло. Теперь сообразим с зелёным:
Тоже плохо. Свешиваем ноги ниже и последовательно берём в компанию «малиновые» и «коричневые» числа:
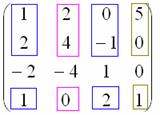
Сначала «синие» с «малиновыми»:
, значит, ранг матрицы не менее трёх. Если бы этот минор оказался равным нулю, то следовало бы вычислить определитель из «синих» и «коричневых» чисел. Других миноров 3-го порядка, которые содержат младший ненулевой минор – нет. И если бы «сине-коричневый» определитель тоже съел бублик, то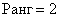 
.
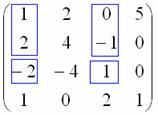
Миноров 3-го порядка на самом деле больше, и рассматриваемый метод в данном случае позволяет сократить вычисления, максимум, до 4-х определителей. Успех нас поджидал на 3-ем шаге, и «хороший» ненулевой минор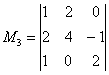 
удостаивается ботинок:
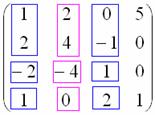
Теперь «синие» и «малиновые» столбцы должны входить во все миноры высших порядков. В данном случае это единственный минор 4-го порядка, совпадающий с определителем матрицы:
(2-ая и 3-я строки пропорциональны – см. свойства определителя)
Если бы у бабушки нас в матрице был пятый столбец, то следовало бы вычислить ещё один минор 4-го порядка («синие», «малиновый» + 5-ый столбец).
Вывод: максимальный порядок ненулевого минора равен трём, значит,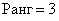 
.
Возможно, не все до конца осмыслили данную фразу: минор 4-го порядка равен нулю, но среди миноров 3-го порядка нашёлся ненулевой – поэтому максимальный порядок ненулевого минора и равен трём.
Возникает вопрос, а почему бы сразу не вычислить определитель? Ну, во-первых, в большинстве заданий матрица не квадратная, а во-вторых, даже если и получится ненулевое значение, то задание будет забраковано, так как необходимо провести стандартное решение «снизу вверх». А в рассмотренном примере нулевой определитель 4-го порядка и вовсе позволяет утверждать, что ранг матрицы лишь меньше 4-х.
Должен признаться, разобранную задачу я придумал сам, чтобы качественнее объяснить метод окаймляющих миноров. В реальной практике всё проще:
Пример 2
Найти ранг матрицы методом окаймляющих миноров
Решение и ответ в конце урока.
Когда алгоритм работает быстрее всего? Вернёмся к той же матрице «четыре на четыре» 
. Очевидно, решение будет самым коротким в случае «хороших» угловых миноров:
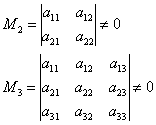
И, если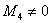 
, то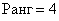 
, в противном случае – .
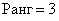Размышление совсем не гипотетично – существует немало примеров, где всё дело и ограничивается только угловыми минорами.
Однако в ряде случаев более эффективен и предпочтителен другой способ:
Date: 2015-07-23; view: 820; Нарушение авторских прав