Ранг любого ненулевого вектора-строки (вектора-столбца) равен единице

И вообще – если в матрице произвольных размеров есть хотя бы один ненулевой элемент, то её ранг не меньше единицы.

Алгебраические векторы-строки и векторы-столбцы в известной степени абстрактны, поэтому снова обратимся к геометрической ассоциации. Ненулевой вектор 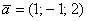задаёт вполне определённое направление в пространстве и годится для построения базиса, поэтому ранг матрицы будем считать равным единице.

Теоретическая справка: в линейной алгебре вектор – это элемент векторного пространства (определяемое через 8 аксиом), который представляет собой строку (или столбец) действительных чисел 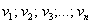. При этом для векторов определена операция умножения на действительное число: 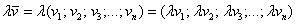и операция сложения: .

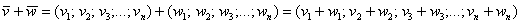Рассмотрим матрицу 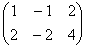, строки которой линейно зависимы (выражаются друг через друга). С геометрической точки зрения во вторую строку записаны координаты коллинеарного вектора 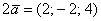, который ничуть не продвинул дело в построении трёхмерного базиса, являясь в этом смысле лишним. Таким образом, ранг данной матрицы тоже равен единице.

Перепишем координаты векторов в столбцы (транспонируем матрицу):

Что изменилось с точки зрения ранга? Ничего. Столбцы пропорциональны, значит, ранг равен единице. Кстати, обратите внимание, что все три строки тоже пропорциональны. Их можно отождествить с координатами трёх коллинеарных векторов плоскости, из которых только один полезен для построения «плоского» базиса. И это полностью согласуется с нашим геометрическим смыслом ранга.

Из вышеприведённого примера следует важное утверждение:

Ранг матрицы по строкам равен рангу матрицы по столбцам. Об этом я уже немного упоминал на уроке об эффективных методах вычисления определителя.

Примечание: из линейной зависимости строк следует линейная зависимость столбцов (и наоборот). Но в целях экономии времени, да и в силу привычки я почти всегда буду говорить о линейной зависимости строк.

Продолжим дрессировать нашего любимого питомца. Добавим в матрицу третьей строкой координаты ещё одного коллинеарного вектора :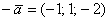

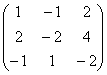
Помог ли он нам в построении трёхмерного базиса? Конечно, нет. Все три вектора гуляют туда-сюда по одной дорожке, и ранг матрицы равен единице. Можно взять сколько угодно коллинеарных векторов, скажем, 100, уложить их координаты в матрицу «сто на три» и ранг такого небоскрёба всё равно останется единичным.

Познакомимся с матрицей , строки которой линейно независимы. Пара неколлинеарных векторов 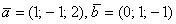пригодна для построения трёхмерного базиса. Ранг этой матрицы равен двум.

А чему равен ранг матрицы ? Строки вроде не пропорциональны…, значит, по идее трём. Однако ранг этой матрицы тоже равен двум. Я сложил первые две строки и записал результат внизу, то есть линейно выразил третью строку через первые две. Геометрически строки матрицы соответствуют координатам трёх компланарных векторов, причём среди этой тройки существует пара неколлинеарных товарищей.

Как видите, линейная зависимость в рассмотренной матрице не очевидна, и сегодня мы как раз научимся выводить её «на чистую воду».

Думаю, многие догадываются, что такое ранг матрицы!

Рассмотрим матрицу 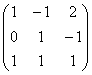, строки которой линейно независимы. Векторы 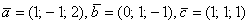образуют аффинный базис, и ранг данной матрицы равняется трём.

Как вы знаете, любой четвёртый, пятый, десятый вектор трёхмерного пространства будет линейно выражаться через базисные векторы. Поэтому, если в матрицу 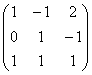добавить любое количество строк, то её ранг всё равно будет равен трём.

Аналогичные рассуждения можно провести для матриц бОльших размеров (понятно, уже без геометрического смысла).

Определение: ранг матрицы – это максимальное количество линейно независимых строк. Или: ранг матрицы – это максимальное количество линейно независимых столбцов. Да, их количество всегда совпадает.

Из вышесказанного также следует важный практический ориентир: ранг матрицы не превосходит её минимальной размерности. Например, в матрице 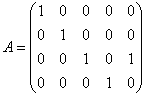четыре строки и пять столбцов. Минимальная размерность – четыре, следовательно, ранг данной матрицы заведомо не превзойдёт 4-х.

Обозначения: в мировой теории и практике не существует общепринятого стандарта для обозначения ранга матрицы, наиболее часто можно встретить: 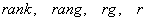– как говорится, англичанин пишет одно, немец другое. Поэтому давайте по мотивам известного анекдота про американский и русский ад обозначать ранг матрицы родным словом. Например: 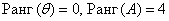. А если матрица «безымянная», коих встречается очень много, то можно просто записать .

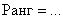Date: 2015-07-23; view: 492; Нарушение авторских прав