Что такое ранг матрицы?

В юмористическом эпиграфе статьи содержится большая доля истины. Само слово «ранг» у нас обычно ассоциируется с некоторой иерархией, чаще всего, со служебной лестницей. Чем больше у человека знаний, опыта, способностей, блата и т.д. – тем выше его должность и спектр возможностей. Выражаясь по молодёжному, под рангом подразумевают общую степень «крутизны».

И братья наши математические живут по тем же принципам. Выведем на прогулку несколько произвольных нулевых матриц:

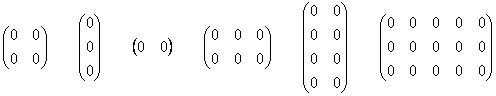
Задумаемся, если в матрице одни нули, то о каком ранге может идти речь? Всем знакомо неформальное выражение «полный ноль». В обществе матриц всё точно так же:

Ранг нулевой матрицы 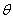любых размеров равен нулю.

Примечание: нулевая матрица обозначается греческой буквой «тета»

В целях лучшего понимания ранга матрицы здесь и далее я буду привлекать на помощь материалы аналитической геометрии. Рассмотрим нулевой вектор 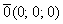нашего трёхмерного пространства, который не задаёт определённого направления и бесполезен для построения аффинного базиса. С алгебраической точки зрения координаты данного вектора записаны в матрицу «один на три» и логично (в указанном геометрическом смысле) считать, что ранг этой матрицы равен нулю.

Теперь рассмотрим несколько ненулевых векторов-столбцов и векторов-строк:

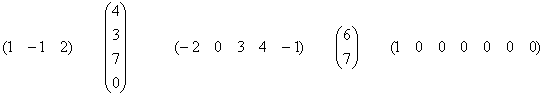
В каждом экземпляре есть хотя бы один ненулевой элемент, и это уже кое-что!

Date: 2015-07-23; view: 459; Нарушение авторских прав