Спектральный метод расчета надежности при перемежающихся отказах

Во всех предыдущих методах расчета надежности предполагалось, что параметры элементов изделия с течением времени изменяются монотонно, такое изменение параметров происходит в следствии старения и износа – этот процесс происходит достаточно медленно и в процессе эксплуатации системы приводит к износу её характеристик. В практике случаются случаи перемежающихся отказов. Последние хотя и длятся короткое время могут приводить к нарушению функций. Причинами перемежающихся отказов – флуктуационные изменения параметров возникают из-за случайных ____________________________________________________________________________.

Рассмотренные выше методы надежности не применимы для случая, когда возникают перемежающие отказы. Расчет надежности в этом случае можно выполнить, что если изменение параметров во времени есть стационарный случайный процесс. При таком предположении выходные характеристики представляются в виде случайных функций, удовлетворяющих условиям верх. процесса.

Если дано и 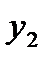, то при условии когда 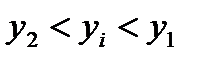- условие возникновения отказа. Среднее число выбросов функции 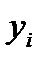за пределы , :

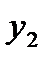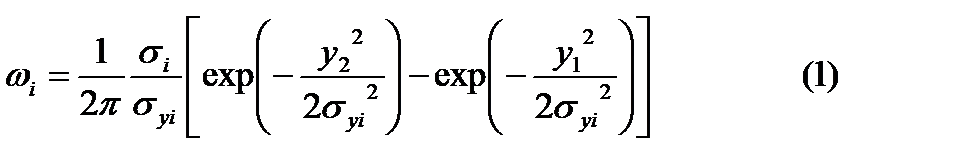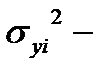, дисперсия выходной характеристики; 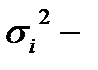производная от корреляционной функции 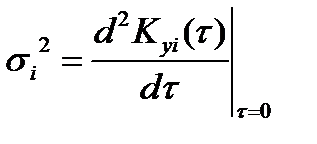,где 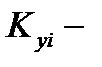корреляционная функция .

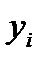По средней частоте отказа можно определить остальные характеристики с помощью известных формул.

Если поток выбросов простейший, то справедлив экспоненциальный закон надежности: 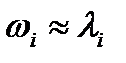. Если распределение амплитудного процесса нормальное, то расчет приходится вести_________________

______________________________________________________________________________________

Из (1) видно, что для 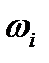необходимо найт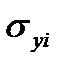и и 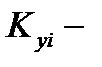эти величины находятся если известны комплектующие параметров.

Если предположить, что корреляционные связи между параметрами отсутствуют и их отклонение относительно средних величин малы, то 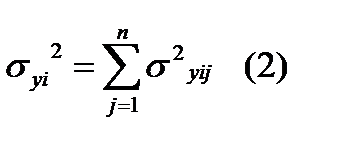, где n – число пар. элементов системы, которые определяют выходную характеристику 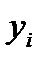. При известных зависимостях изменения параметров во времени можно найти через спектральную плотность (Sj):

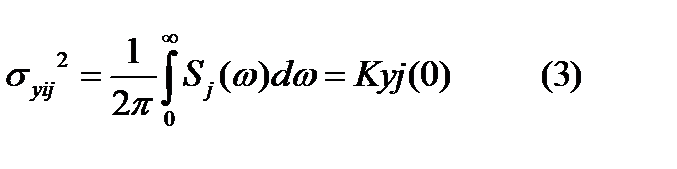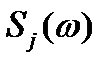, где и 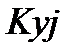- спектральная плотность и корреляционная функция случайного процесса изменения j-го элемента.

При известной реализации процесса спектральную плотность можно вычислить с помощью коррелятора.

При аналитическом способе первоначально вычисляются корреляционна функция, затем она аппраксимируется и вычисляется спектральная плотность и с помощью преобразования Фурье определяется величина: 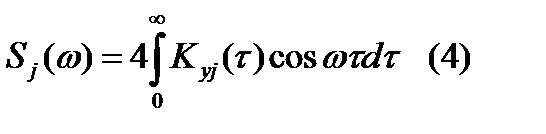. На основе(2) и (3): 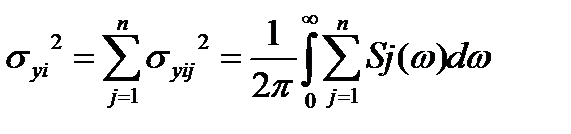, 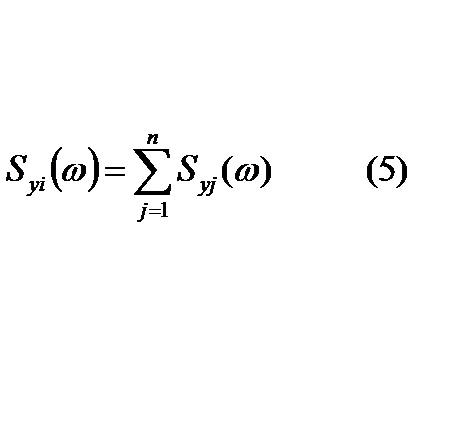. Тогда корреляционная функция может быть определена по спектральной плотности с помощью обратного преобразования Фурье: 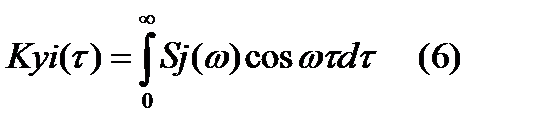. Спектральный метод расчета практически дает возможность аналитически _________ при условии когда имеется ограниченное число параметров. Удобно применять для простых систем. Но с ростом числа элементов в сумме 5- с использованием ЭВМ.

Недостатки:

1. Метод не учитывает корреляционные связи между параметрами;

2. Трудность вычисления основных характеристик надежности в случае если поток отказа не является простейшим. В этом случае частота отказа будет функцией времени если поток параметров не стационарен.

3. Метод не позволяет учитывать влияние внезапных и постепенных отказов на перемежающиеся отказы.

Date: 2015-07-23; view: 466; Нарушение авторских прав