Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Частота отказов, средняя частота отказов элементов, их основные свойства. Достоинства и недостатки средней частоты отказов элементов
|
|
Частота отказов – называется отношение числа отказавших образцов в единицу времени к числу образцов установленных первоначально на испытании. При условии, что отказавшие образца не восстанавливаются и не заменяются исправными. Число отказавших образцов в интервал времени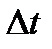 
может зависеть от промежутка времени: 
.
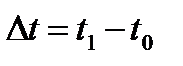Поэтому частота отказов является функцией времени: 
, 
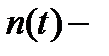число отказавших образцов в интервал времени от 
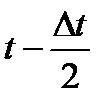до 
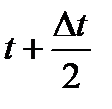. Равенство (1) является статистическим определением частоты отказов. Величина 
, 
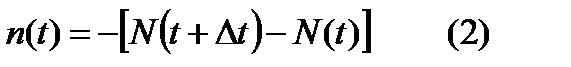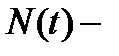число образцов исправно работающих к моменту времени t. 
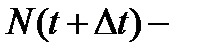число к моменту времени 
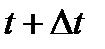. Если число N0 большое, то справедливо соотношение: 
.
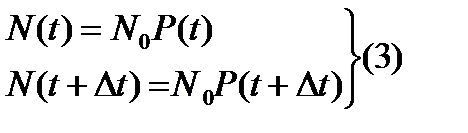Подставляя (2) в (1) и учитывая (3) получим: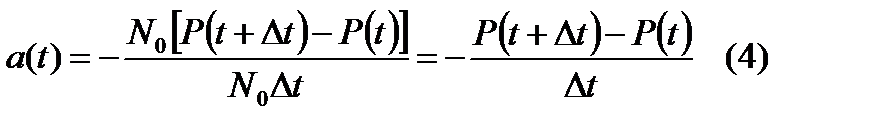 
.
При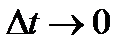 
: 
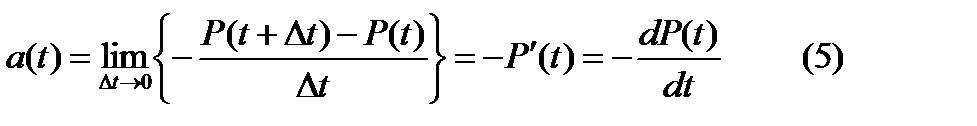. Таким образом частота отказов есть первая производная от функции безотказной работы.
, 
.
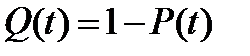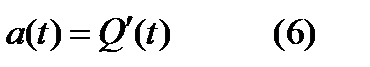Средняя частота отказов – называется отношение числа отказавших образцов или элементов в единицу времени к числу испытывающих образцов при условии, что все образцы, вышедшие из строя заменяются исправными (новыми или образцовыми).
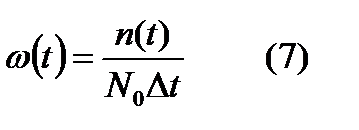, где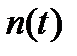 
- число отказавших образцов в интервале времени от 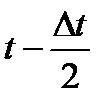до 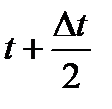, N0 - число испытываемых образцов (N0=const), 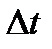- интервал времени.
Пусть в момент времени t=0 на испытании находится N0 образцов и пусть по мере выхода из строя они заменяются новыми. Тогда средне число отказавших образцов в любой промежуток времени: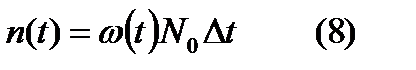 
. Величина 
, 
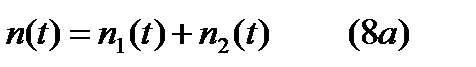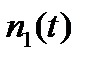- число отказавших образцов из числа тех которые поставлены на испытания в момент времени t=0; 
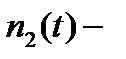число отказавших образцов из числа замененных в процессе испытания за время от 0 до t. Величина 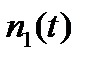определяется через частоту отказов: 
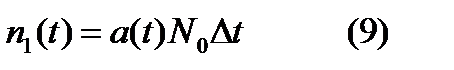. Для определения величины 
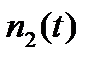рассмотрим промежуток времени 
, 
. 
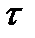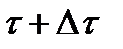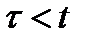, очевидно в этом промежутке выйдет из строя 
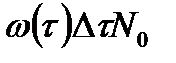в промежутке 
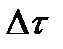. Эти образцы будут заменены и в промежутке 
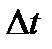из их числа в среднем откажут: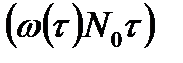 
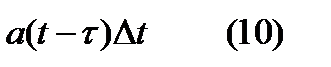, тогда для определения 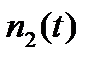необходимо проссумировать (10) по всем промежуткам 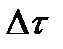предшествующих t: 
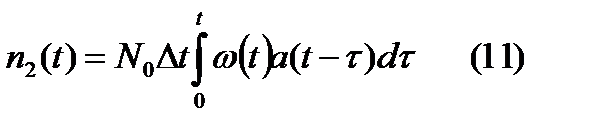, подставляя (11), (9) в (8) и сокращая на 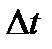получим: 
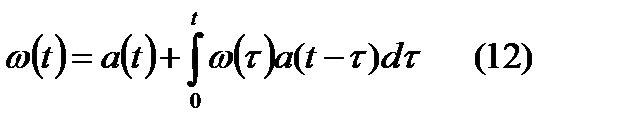- классическое уравнение для определения средней частоты отказа (уравнение Вольтерра).
В операторной форме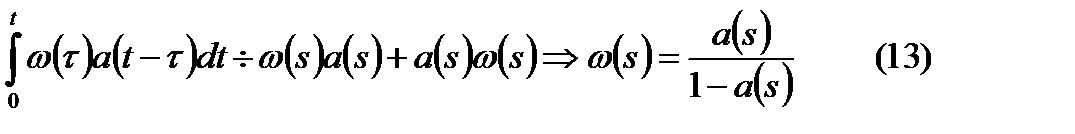 
.
Уравнение (12) позволяет сделать выводы:
1) 
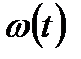всегда больше 
(
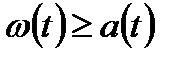), так как 
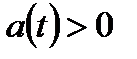, а интеграл 
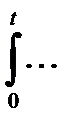не может быть отрицательной величиной.
2) Не зависимо от вида функци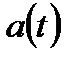и 
при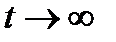 
средняя частота отказа стремится к постоянному значению (
).
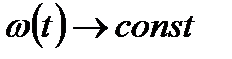Основное достоинство средней частоты отказа :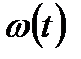
1) Она позволяет полно оценить свойство изделия, работающего в режиме смены элементов;
2) Она может быть использована для оценки надежности системы разового применения в процессе их хранения;
3) Позволяет определить число отказавших в изделии элементов, что позволяет прогнозировать необходимое число элементов нуждающихся в замене в период эксплуатации за время t;
4) Она позволяет правильно спланировать частоту профилактических работ в течение t.
Недостаток: сложность её определения и соответствие вероятности безотказной работы.
Date: 2015-07-23; view: 708; Нарушение авторских прав