Последовательное, параллельное и параллельно-последовательное соединение элементов

Последовательное соединение элементов - называется такое соединение, при котором отказ одного элемента приводит к отказу остальных элементов.

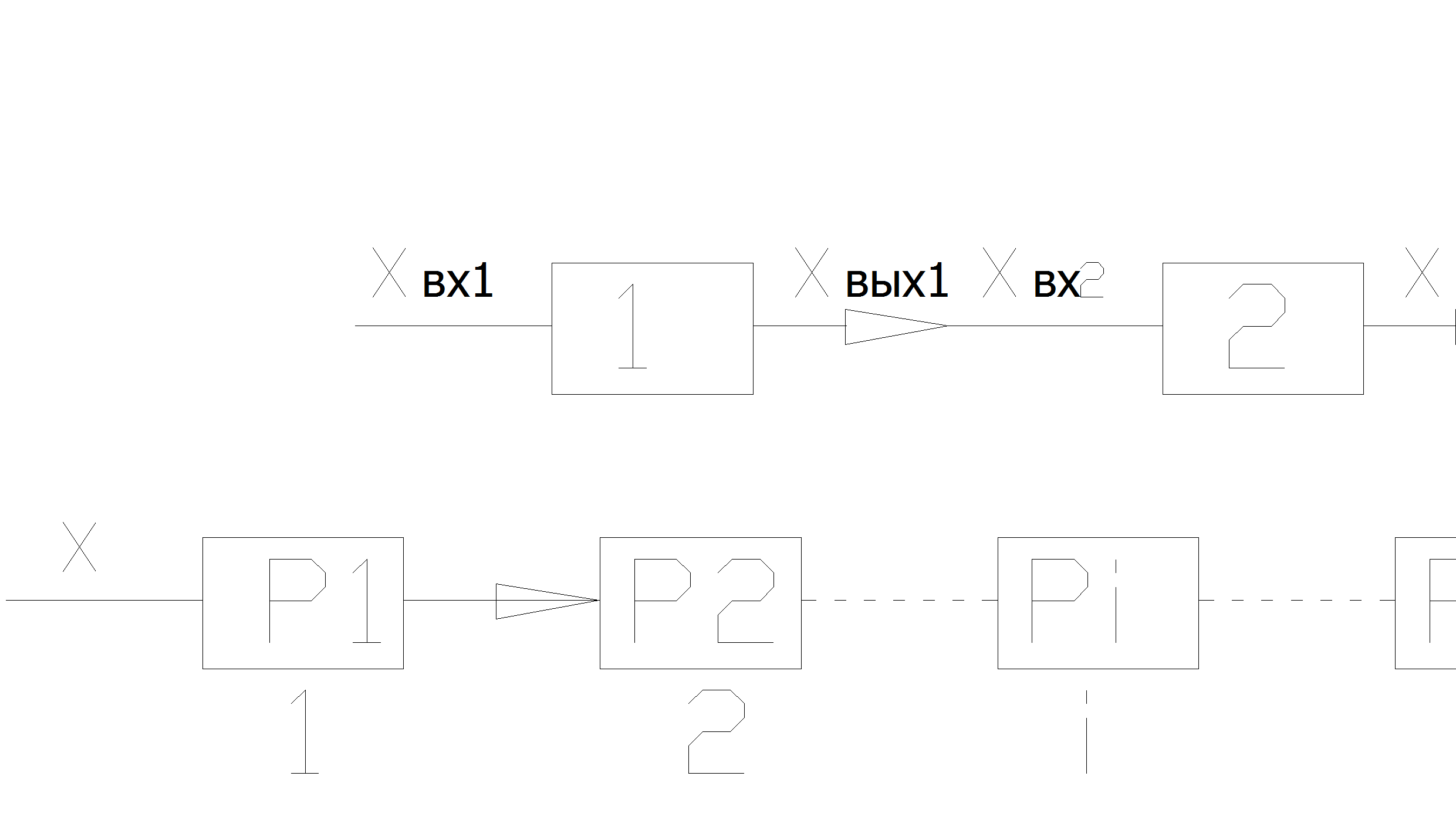Техническое понятие последовательного соединения может не совпадать с понятием в смысле надежности. Условимся считать, что вероятность безотказной работы одних элементов не зависит от вероятности безотказной работы других элементов, т.е. отказ или изменение одной группы элементов не зависит и не влияет на вероятность безотказной работы других в этом случае элементы называются независимыми, для последовательного соединения элементов вероятность безотказной работы определяется согласно теорем вероятности:

. Согласно (1) результирующая надежность при последовательном соединение есть произведение вероятностей безотказной работы отдельных элементов: . , 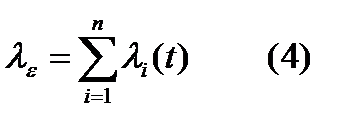. Из (2), (3), (4) следует, что при последовательном соединении элементов интенсивности отказов складываются. Интенсивность отказа соединения есть сумма интенсивностей отказов отдельных элементов.

Интенсивность отказа последовательного соединения всегда больше любого из этих элементов. Это приводит к тому, что вероятность безотказной работы последовательного соединения всегда меньше вероятности самого надежного элемента в этой системе.

При экспоненциальном законе надежности: , 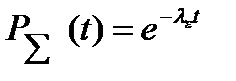. Среднее время при экспоненциальном законе надежности: . Если элементы соединения имеют одинаковую интенсивность отказов , то в этом случае вероятность безотказной работы: 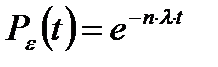, где n – число элементов в соединении. Тогда средняя наработка .

Предположим, что требуется найти вероятность безотказной работы соединения из 4-х элементов. 2 из которых имеют экспоненциальную функцию надежности, а 2 – подчиняются закону Вейбулла.

- экспоненциальный закон надежности;

- закон распределения Вейбулла.

Тогда суммарная безотказность работы всего соединения будет равна:

, , если подставить в последнее равенство , то можно найти вероятность безотказной работы соединения.

Может быть решена и обратная задача. Пусть задана вероятность безотказной работы. Требуется определить какая допустимая при этом суммарная интенсивность. Все элементы имеют экспоненциальный закон надежности. , , .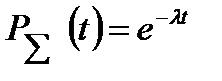

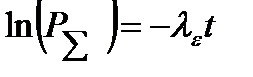Параллельное в смысле надежности называется такое соединение элементов, когда отказ всего соединения наступит тогда, когда отказывают все элементы, входящие в соединение.

При расчете надежности предполагается, что элементы являются независимыми, т.е. отказ одного из них не влияет на работу других.

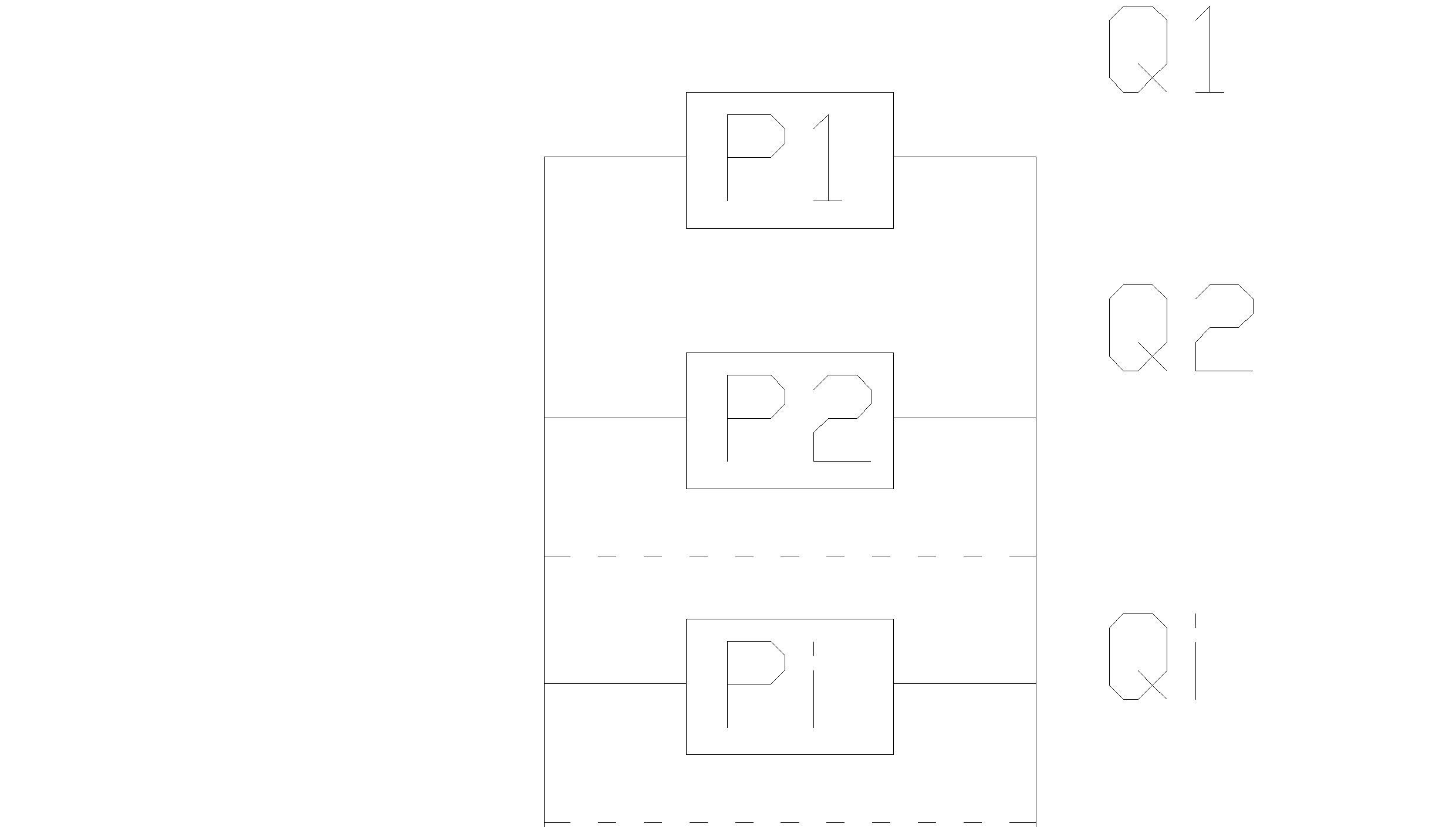
Вероятность отказа всего соединения произойдет в случае отказа всего соединения: 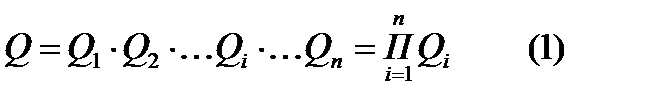, Вероятность отказа системы согласно (1) равна произведению отказов всех его элементов. Вероятность безотказной системы: . В случае когда вероятность безотказной работы отдельных элементов подчиняются экспоненциальному закон надежности:

. Из (4) следует, что функция надежности параллельного соединения элементов, в отличие от последовательного соединения, при экспоненциальной функции отдельных элементов уже не является экспоненциальным законом, если функции надежности элементов одинаковы. , , , .

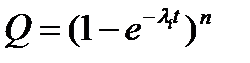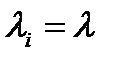При экспоненциальном законе надежности: , , , . Математическое ожидание при экспоненциальном законе надежности:

. Если продолжительность времени работы системы не велико, так что произведение интенсивностей отказов на время работы много меньше 1, то можно считать: , , 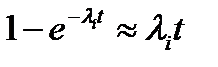тогда сохраняя два первых члена в разложении экспоненты получим, что вероятность безотказной работы равна: , .

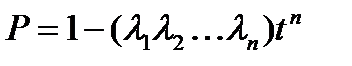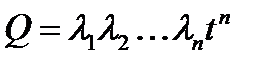Параллельно-последовательное соединение элементов. Наиболее распространенными являются 2 схемы параллельно- последовательного соединения.

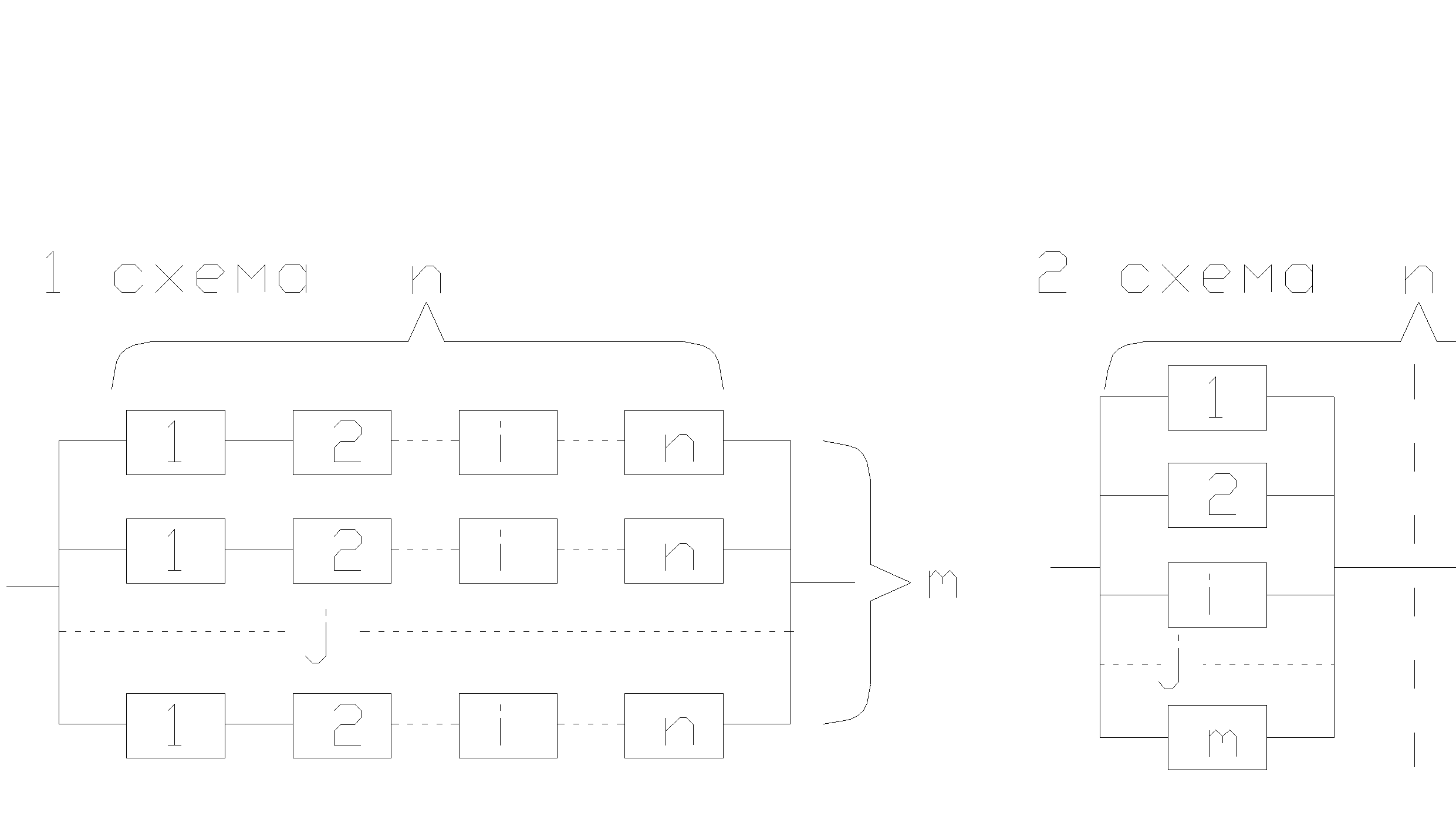В 1 –ой схеме имеется m параллельных цепей по n одинаковых элементов в каждой цепи. Элементы как и прежде считаются независимыми.

Вероятность безотказной работы каждой j цепи: . Вероятность безотказной работы всей схемы: .

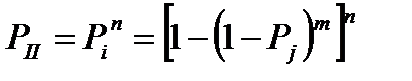Во второй схеме n последовательно соединенных групп, состоящие из m одинаковых параллельно соединенных элементов. . Тогда для всей схемы: . В большинстве случаев при практических расчетах сложные схемы можно разбить на части, состоящие из простейших соединений. При составлении структурной схемы надежности в качестве отдельных элементов могут быть взяты элементарные звенья или целые узлы. Если у этих узлов известны характеристики надежности.

Date: 2015-07-23; view: 11417; Нарушение авторских прав